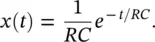
Find the Fourier spectrum representation of this transient response.
Substituting x ( t ) into Eq. (1.6)we obtain

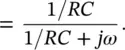
Therefore,
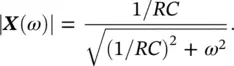
The transient response and its Fourier spectrum are shown in Figure 1.6.
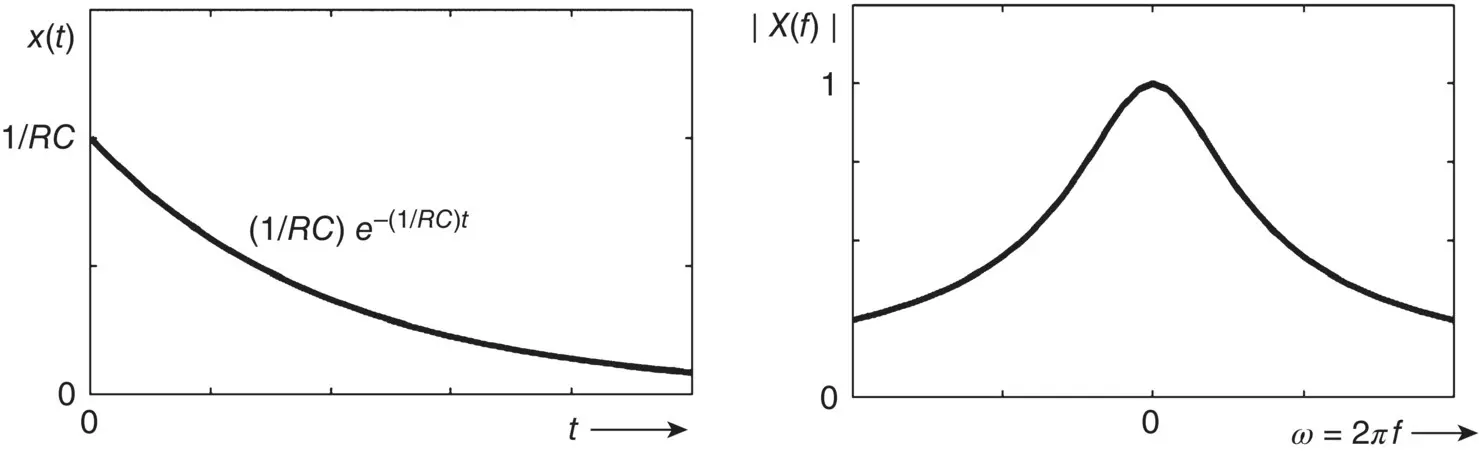
Figure 1.6 Time and frequency domain representations of the transient response of an R–C series circuit.
The impulse response of a dynamic system is its output in response to a brief input pulse signal, called an impulse. The impulse response of the damped vibration of a one‐degree‐of‐freedom mass‐spring system of mass M , stiffness K , and coefficient of damping R (see Chapter 2of this book) is given by
where A = ( Mω d) −1, α = R /2 M and λ = ω dis known as the damped “natural” angular frequency. Find the Fourier spectrum representation of this impulse response.
Using the mathematical property e jθ= cos θ + j sin θ , we can write
 . Then, Eq. (1.6)is
. Then, Eq. (1.6)is
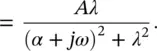
The impulse response and its Fourier spectrum are shown in Figure 1.7. We notice that replacing α and λ by the corresponding values in terms of the stiffness K , mass M , and damping constant R , of the damped mass‐spring system, the Fourier spectrum becomes (compare with Eq. (2.18))
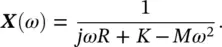
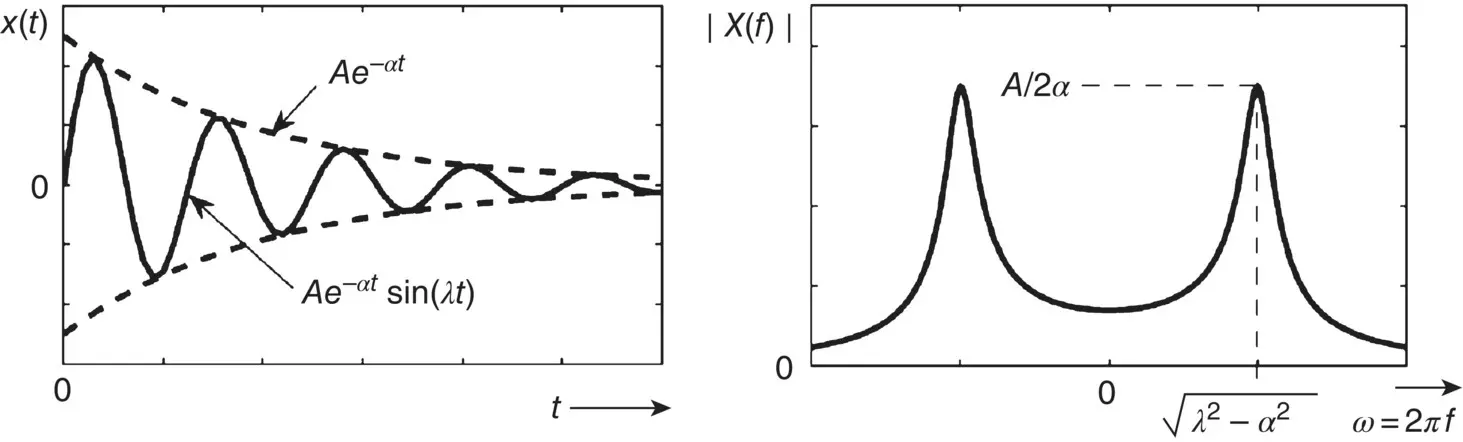
Figure 1.7 Time and frequency domain representations of the transient response of the impulse response of a damped vibration of a mass‐spring system.
In the case of the pure tone a useful quantity to determine is the mean square value, i.e. the time average of the signal squared 〈 x 2( t )〉 t[8]
(1.7) 
where 〈〉 tdenotes a time average.
For the pure tone in Figure 1.2a then we obtain
(1.8) 
where A is the signal amplitude.
The root mean square value is given by the square root of 〈 x 2( t )〉 tor
(1.9) 
For the general case of the complex pure tone in Eq. (1.1)or (1.2)we obtain:
(1.10) 
or
(1.11) 
since 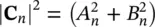 . The mean square value then is the sum of the squares of all the harmonic components of the wave weighted by a constant of 1/2.
. The mean square value then is the sum of the squares of all the harmonic components of the wave weighted by a constant of 1/2.
Determine the mean square and rms values of the signal in Figure 1.3.
We can use Eq. (1.7)to determine its mean square value,
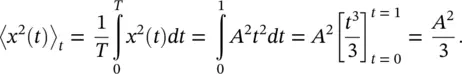
The same result is obtained from its Fourier series representation using Eq. (1.10):
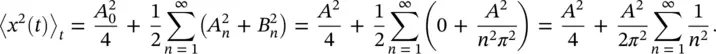
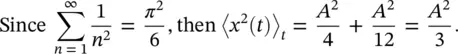
Recalling that the root mean square value is given by the square root of the mean square value, the rms value of this saw tooth signal is 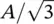 . Note the difference between the rms value obtained in this example and that in Eq. (1.9)for a sine wave.
. Note the difference between the rms value obtained in this example and that in Eq. (1.9)for a sine wave.
1.3.5 Energy and Power Spectral Densities
In the case of nonperiodic signals (see Section 1.3.2), a quantity called the energy density function or equivalently the energy spectral density , S ( f ), is defined:
(1.12) 
The energy spectral density S ( f ) is the “energy” of the sound or vibration signal in a bandwidth of 1 Hz. Note that S ( ω ) = 2 πS ( f ) where S ( ω ) is the “energy” in a 1 rad/s bandwidth. We use the term “energy” because if x ( t ) were converted into a voltage signal, S ( ω ) would have the units of energy if the voltage were applied across a 1 Ω resistor. In the case of the pure tone, if x ( t ) is assumed to be a voltage, then the mean square value in Eq. (1.8)represents the power in watts.
Читать дальше

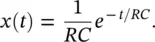

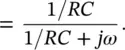
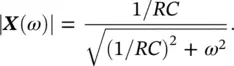

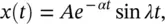
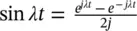 . Then, Eq. (1.6)is
. Then, Eq. (1.6)is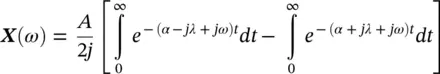
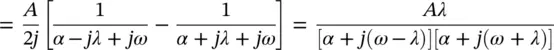
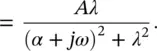
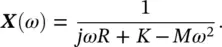






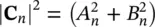 . The mean square value then is the sum of the squares of all the harmonic components of the wave weighted by a constant of 1/2.
. The mean square value then is the sum of the squares of all the harmonic components of the wave weighted by a constant of 1/2.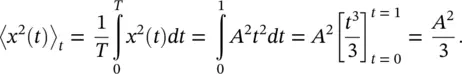
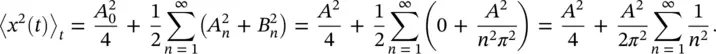
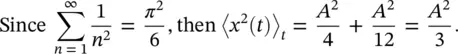
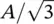 . Note the difference between the rms value obtained in this example and that in Eq. (1.9)for a sine wave.
. Note the difference between the rms value obtained in this example and that in Eq. (1.9)for a sine wave.











