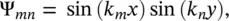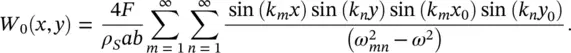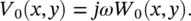Malcolm J. Crocker - Engineering Acoustics

For example, for a simply‐supported rectangular plate, the distribution Ψ mn(see Eq. (2.69)) is

(2.76)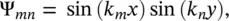

and γ = 1/4. Then, we can obtain that for a point force F concentrated at the point ( x 0, y 0)

(2.76)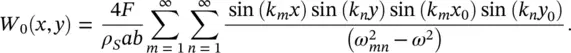

The vibration velocity distribution on the rectangular plate can be obtained as

(2.77)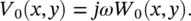

In practice, to calculate the plate response to a concentrated force, it is necessary to truncate the infinite summation. More complicated cases of boundary conditions have been studied in the literature [19].

All the theory presented above and the subsequent applications have been developed assuming light fluid loading, so that the plate response is not affected by the surrounding environment, which acts as added mass and radiation damping [20]. This criterion is not valid for submerged structures.

The numerical results for the velocity level at the coordinate point ( x,y ) = (0.04, 0.03) for a plywood board with properties E = 6 × 10 9N/m 2, ρ S= 6.5 kg/m 2, a × b = 0.7 × 0.6 m 2, ν = 0.293 and η = 0.01 are presented in Figure 2.19. The reference velocity is 10 −18(m/s) 2. It is observed that excitation close to a corner excites more modes in the plate. Excitation at the middle point of the plate excites mostly the modes ( m,n ) where m and n are both even, while no contribution to the velocity level is included from modes having nodal lines passing through the center of the plate.

Figure 2.19 Computed velocity level of a simply‐supported rectangular plate excited: ______ at a corner; _ _ _ _ at the center.

( Source: from Ref. [16].)

1 1 Bies, D.A. and Hansen, C.H. (2003). Engineering Noise Control–Theory and Practice, 3e. London: E & FN Spon.

2 2 Bell, L.H. (1982). Industrial Noise Control – Fundamentals and Applications. New York: Marcel Decker.

3 3 Hall, D.E. (1987). Basic Acoustics. New York: Wiley.

4 4 Kinsler, L.E., Frey, A.R., Coppens, A.B., and Sanders, J.V. (1999). Fundamentals of Acoustics, 4e. New York: Wiley.

5 5 Fahy, F.J. and Walker, J.G. (eds.) (1998). Fundamentals of Noise and Vibration. London: E & FN Spon.

6 6 Lighthill, M.J. (1978). Waves in Fluids. Cambridge: Cambridge University Press.

7 7 Pierce, A.D. (1981). Acoustics: An Introduction to Its Physical Properties and Applications. New York: McGraw‐Hill (reprinted by the Acoustical Society of America, 1989).

8 8 Inman, D.J. (2007). Passive damping. In: Handbook of Noise and Vibration Control (ed. M.J. Crocker), 225–231. New York: Wiley.

9 9 Ungar, E.E. (2007). Damping of structures and use of damping materials. In: Handbook of Noise and Vibration Control (ed. M.J. Crocker), 734–744. New York: Wiley.

10 10 Shabana, A.A. (1997). Vibration of Discrete and Continuous Systems, 2e. New York: Springer‐Verlag.

11 11 Meirovitch, L. (2001). Fundamentals of Vibrations. New York: McGraw‐Hill.

12 12 Lalor, N. (1998). Fundamentals of vibration. In: Fundamentals of Noise and Vibration (eds. F.J. Fahy and J. Walker), 61–114. London: E & FN Spon.

13 13 Kelly, S.G. (2000). Fundamentals of Mechanical Vibrations, 2e. McGraw‐Hill.

14 14 Leissa, A.W. (1993). Vibration of Plates. New York: Acoustical Society of America.

15 15 Berry, A., Guyader, J.L., and Nicolas, J. (1990). A general formulation for the sound radiation from rectangular, baffled plates with arbitrary boundary conditions. J. Acoust. Soc. Am. 88: 2792–2802.

16 16 Arenas, J.P. (2001) Analysis of the acoustic radiation resistance matrix and its applications to vibro‐acoustic problems. PhD thesis. Auburn University.

17 17 Blevins, R.D. (2015). Formulas for Dynamics, Acoustics and Vibration. New York: Wiley.

18 18 Malecki, I. (1969). Physical Foundations of Physical Acoustics. Oxford: Pergamon Press.

19 19 Arenas, J.P. (2003). On the vibration analysis of rectangular clamped plates using the virtual work principle. J. Sound Vib. 266: 912–918.

20 20 Tao, J.S., Liu, G.R., and Lam, K.Y. (2001). Sound radiation of a thin infinite plate in light and heavy fluids subject to multi‐point excitation. Appl. Acoust. 62: 573–587.

The fluid mechanics equations, from which the acoustics equations and results may be derived, are quite complicated. However, because most acoustical phenomena involve very small perturbations from steady‐state conditions, it is possible to make significant simplifications to these fluid equations and to linearize them. The results are the equations of linear acoustics. The most important equation, the wave equation, is presented in this chapter together with some of its solutions. Such solutions give the sound pressure explicitly as functions of time and space, and the general approach may be termed the wave acoustics approach. This chapter presents some of the useful results of this approach but also briefly discusses some of the other alternative approaches, sometimes termed ray acoustics and energy acoustics, that are used when the wave acoustics approach becomes too complicated. The main purpose of this chapter is to present some of the most important acoustics formulas and definitions, without derivation, which are used in the other chapters of this book.

Some of the basic concepts of acoustics and sound wave propagation used throughout the rest of this book are discussed here. For further discussion of some of these basic concepts and/or a more advanced mathematical treatment of some of them, the reader is referred to the Handbook of Acoustics [1] and other texts [2–18] which are also useful for further discussion on fundamentals and applications of the theory of noise and vibration problems.

Wave motion is easily observed in the waves on stretched strings and as ripples on the surface of water. Waves on strings and surface water waves are very similar to sound waves in air (which we cannot see), but there are some differences that are useful to discuss. If we throw a stone into a calm lake, we observe that the water waves ( ripples ) travel out from the point where the stone enters the water. The ripples spread out circularly from the source at the wave speed, which is independent of the wave height.

Somewhat like the water ripples, sound waves in air travel at a constant speed, which is proportional to the square root of the absolute temperature and is almost independent of the sound wave strength. The wave speed is known as the speed of sound. Sound waves in air propagate by transferring momentum and energy between air particles. Sound wave motion in air is a disturbance that is imposed onto the random motion of the air molecules (known as Brownian motion). The mean speed of the molecular random motion and rate of molecular interaction increases with the absolute temperature of the gas. Since the momentum and sound energy transfer occurs through the molecular interaction, the sound wave speed is dependent solely upon the absolute temperature of the gas and not upon the strength of the sound wave disturbance. There is no net flow of air away from a source of sound, just as there is no net flow of water away from the source of water waves. Of course, unlike the waves on the surface of a lake, which are circular or two‐dimensional, sound waves in air in general are spherical or three‐dimensional.