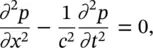As water waves move away from a source, their curvature decreases, and the wavefronts may be regarded almost as straight lines. Such waves are observed in practice as breakers on the seashore. A similar situation occurs with sound waves in the atmosphere. At large distances from a source of sound, the spherical wavefront curvature decreases, and the wavefronts may be regarded almost as plane surfaces.
Plane sound waves may be defined as waves that have the same acoustical properties at any position on a plane surface drawn perpendicular to the direction of propagation of the wave. Such plane sound waves can exist and propagate along a long straight tube or duct (such as an air‐conditioning duct). In such a case, the waves propagate in a direction along the duct axis and the plane wave surfaces are perpendicular to this direction (and are represented by duct cross‐sections). Such waves in a duct are one‐dimensional, like the waves traveling along a long string or rope under tension (or like the ocean breakers described above).
Although there are many similarities between one‐dimensional sound waves in air, waves on strings, and surface water waves, there are some differences. In a fluid such as air, the fluid particles vibrate back and forth in the same direction as the direction of wave propagation; such waves are known as longitudinal, compressional, or sound waves. On a stretched string, the particles vibrate at right angles to the direction of wave propagation; such waves are usually known as transverse waves. The surface water waves described are partly transverse and partly longitudinal, with the complication that the water particles move up and down and back and forth horizontally. (This movement describes elliptical paths in shallow water and circular paths in deep water. The vertical particle motion is much greater than the horizontal motion for shallow water, but the two motions are equal for deep water.) The water wave direction is, of course, horizontal.
Surface water waves are not compressional (like sound waves) and are normally termed surface gravity waves. Unlike sound waves, where the wave speed is independent of frequency, long‐wavelength surface water waves travel faster than short‐wavelength waves, and thus water wave motion is said to be dispersive. Bending waves on beams, plates, cylinders, and other engineering structures are also dispersive. There are several other types of waves that can be of interest in acoustics: shear waves, torsional waves, and boundary waves (see chapter 12 in the Encyclopedia of Acoustics [19]), but the discussion here will concentrate on sound wave propagation in fluids.
The propagation of sound may be illustrated by considering gas in a tube with rigid walls and having a rigid piston at one end. The tube is assumed to be infinitely long in the direction away from the piston. We shall assume that the piston is vibrating with simple harmonic motion at the left‐hand side of the tube (see Figure 3.1) and that it has been oscillating back and forth for some time. We shall only consider the piston motion and the oscillatory motion it induces in the fluid from when we start our clock. Let us choose to start our clock when the piston is moving with its maximum velocity to the right through its normal equilibrium position at x = 0. See the top of Figure 3.1, at t = 0. As time increases from t = 0, the piston straight away starts slowing down with simple harmonic motion, so that it stops moving at t = T /4 at its maximum excursion to the right. The piston then starts moving to the left in its cycle of oscillation, and at t = T /2 it has reached its equilibrium position again and has a maximum velocity (the same as at t = 0) but now in the negative x direction. At t = 3 T /4, the piston comes to rest again at its maximum excursion to the left. Finally at t = T the piston reaches its equilibrium position at x = 0 with the same maximum velocity we imposed on it at t = 0. During the time T , the piston has undergone one complete cycle of oscillation. We assume that the piston continues vibrating and makes f oscillations each second, so that its frequency f = 1 /T (Hz).
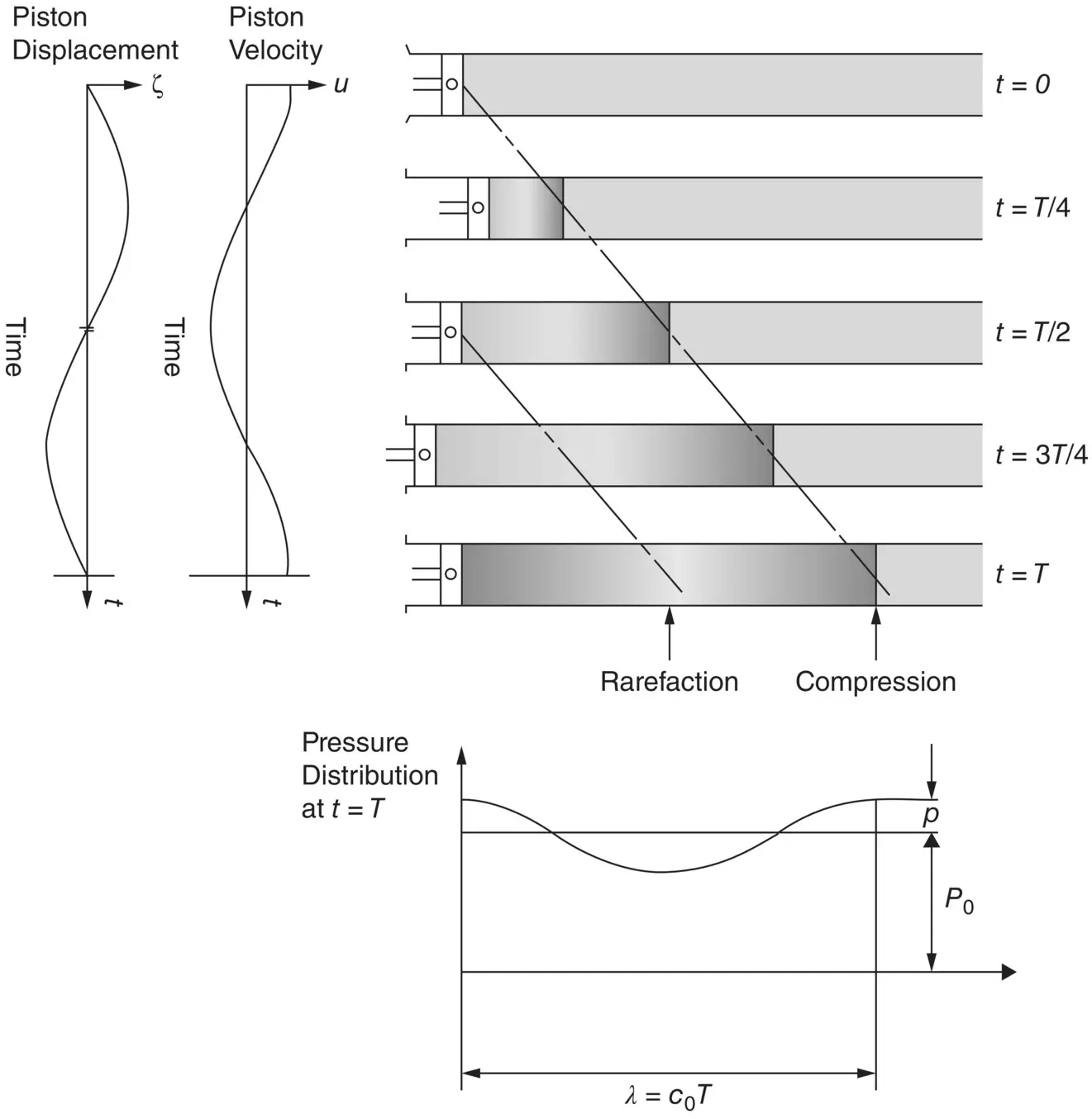
Figure 3.1 Schematic illustration of the sound pressure distribution created in a tube by a piston undergoing one complete simple harmonic cycle of operation in period T seconds.
As the piston moves backward and forward, the gas in front of the piston is set into motion. As we all know, the gas has mass and thus inertia and it is also compressible. If the gas is compressed into a smaller volume, its pressure increases. As the piston moves to the right, it compresses the gas in front of it, and as it moves to the left, the gas in front of it becomes rarified. When the gas is compressed, its pressure increases above atmospheric pressure, and, when it is rarified, its pressure decreases below atmospheric pressure. The pressure difference above or below the atmospheric pressure, p 0, is known as the sound pressure, p , in the gas. Thus the sound pressure p = p tot– p 0, where p totis the total pressure in the gas. If these pressure changes occurred at constant temperature, the fluid pressure would be directly proportional to its density, ρ , and so p/ρ = constant. This simple assumption was made by Sir Isaac Newton, who in 1660 was the first to try to predict the speed of sound. But we find that, in practice, regions of high and low pressure are sufficiently separated in space in the gas (see Figure 3.1) so that heat cannot easily flow from one region to the other and that the adiabatic law, p/ρ γ= constant, is more closely followed in nature.
As the piston moves to the right with maximum velocity at t = 0, the gas ahead receives maximum compression and maximum increase in density, and this simultaneously results in a maximum pressure increase. At the instant the piston is moving to the left with maximum negative velocity at t = T /2, the gas behind the piston, to the right, receives maximum rarefaction, which results in a maximum density and pressure decrease. These piston displacement and velocity perturbations are superimposed on the much greater random motion of the gas molecules (known as the Brownian motion). The mean speed of the molecular random motion in the gas depends on its absolute temperature. The disturbances induced in the gas are known as acoustic (or sound) disturbances. It is found that momentum and energy pulsations are transmitted from the piston throughout the whole region of the gas in the tube through molecular interactions (sometimes simply termed molecular collisions).
If a disturbance in a thin cross‐sectional element of fluid in a duct is considered, a mathematical description of the motion may be obtained by assuming that (i) the amount of fluid in the element is conserved, (ii) the net longitudinal force is balanced by the inertia of the fluid in the element, (iii) the compressive process in the element is adiabatic (i.e. there is no flow of heat in or out of the element), and (iv) the undisturbed fluid is stationary (there is no fluid flow). Then the following equation of motion may be derived:
(3.1) 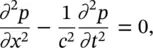
Читать дальше