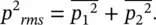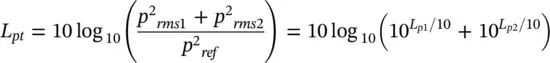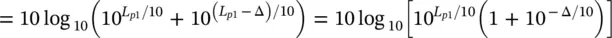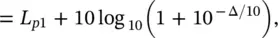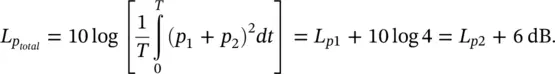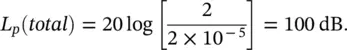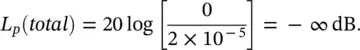The decibel (dB) is the ratio R 1given by
(3.21) 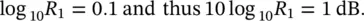
Thus, R 1= 10 0.1= 1.26. The decibel is seen to represent the ratio 1.26. A larger ratio, the bel , is sometimes used. The bel is the ratio R 2given by log 10 R 2= 1. Thus, R 2= 10 1= 10. The bel represents the ratio 10 and is thus much larger than a decibel. For simplicity, in the following sections of this book we denote log( ) = log 10( ).
3.4.1 Sound Pressure Level
The sound pressure level L pis given by
(3.22) 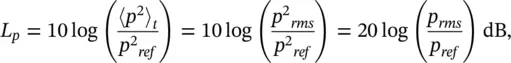
where p refis the reference pressure, p ref= 20 μ Pa = 0.00002 N/m 2(= 0.0002 μ bar) for air. This reference pressure was originally chosen to correspond to the quietest sound (at 1000 Hz) that the average young person can hear. The sound pressure level is often abbreviated as SPL. Figure 3.4shows some sound pressure levels of typical sounds.

Figure 3.4 Some typical sound pressure levels, L p.
The sound power level of a source, L W, is given by
(3.23) 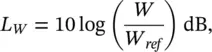
where W is the sound power of a source and W ref= 10 −12W is the reference sound power.
Some typical sound power levels are given in Figure 3.5.
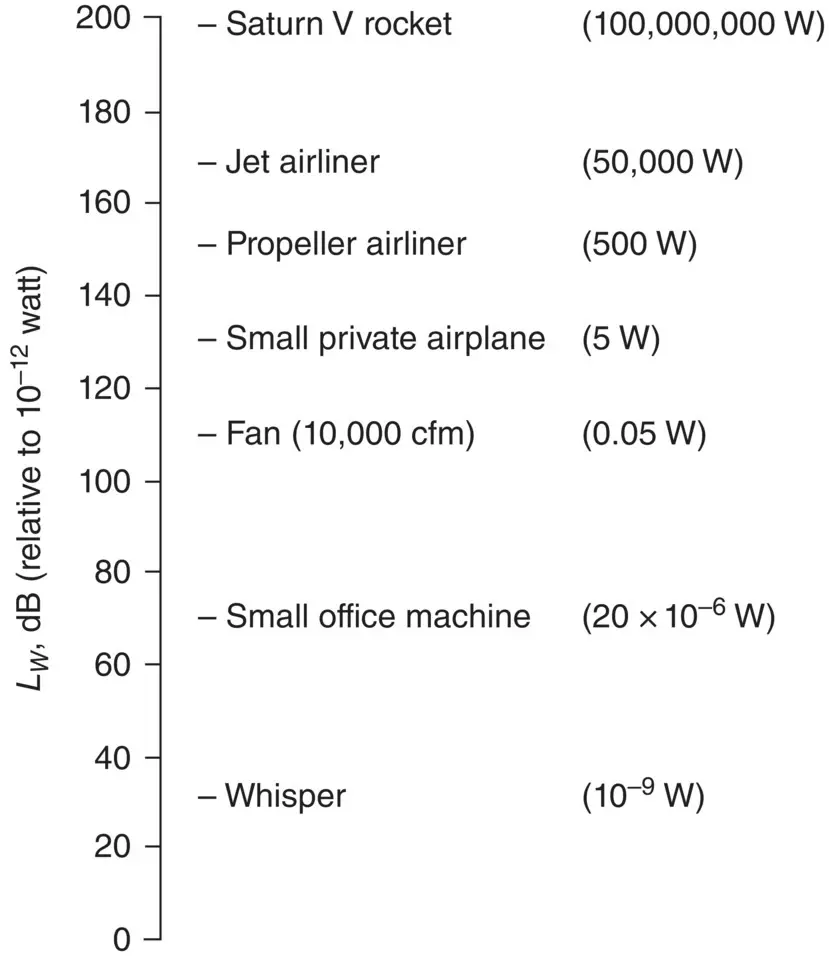
Figure 3.5 Some typical sound power levels, L W.
3.4.3 Sound Intensity Level
The sound intensity level L Iis given by
(3.24) 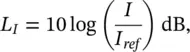
where I is the component of the sound intensity in a given direction and I ref= 10 −12W/m 2is the reference sound intensity.
3.4.4 Combination of Decibels
If the sound pressures p 1and p 2at a point produced by two independent sources are combined, the mean square pressure is
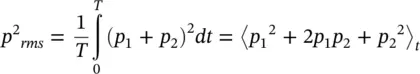
(3.25) 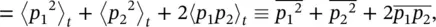
where 〈〉 tand the overbar indicate the time average 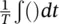 .
.
Except for some special cases, such as two pure tones of the same frequency or the sounds from two correlated sound sources, the cross term 2〈 p 1 p 2〉 tdisappears if T → ∞. Then in such cases the mean square sound pressures 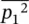 and
and 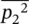 are additive, and the total mean square sound pressure at some point in space, if they are completely independent noise sources, may be determined using Eq. (3.26).
are additive, and the total mean square sound pressure at some point in space, if they are completely independent noise sources, may be determined using Eq. (3.26).
(3.26) 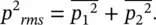
Let the two mean square pressure contributions to the total noise be p 2 rms1and p 2 rms2corresponding to sound pressure levels L p1and L p2, where L p2= L p1− Δ. The total sound pressure level is given by the sum of the individual contributions in the case of uncorrelated sources, and the total sound pressure level is given by forming the total sound pressure level by taking logarithms of Eq. (3.26)
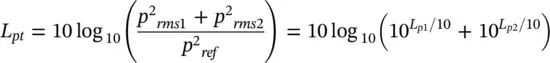
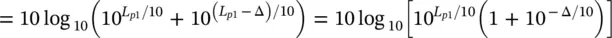
(3.27) 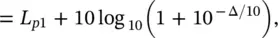
where L ptis the combined sound pressure level due to both sources, L p1is the greater of the two sound pressure level contributions, and Δ is the difference between the two contributions, all in dB. Equation (3.27)is presented in Figure 3.6.
If two independent noise sources each create sound pressure levels operating on their own of 80 dB, at a certain point, what is the total sound pressure level?
The difference in levels is 0 dB; thus the total sound pressure level is 80 + 3 = 83 dB.
If two independent noise sources have sound power levels of 70 and 73 dB, what is the total level?
The difference in levels is 3 dB; thus the total sound power level is 73 + 1.8 = 74.8 dB.
Figure 3.6and these two examples do not apply to the case of two pure tones of the same frequency.
Note: For the special case of two pure tones of the same amplitude and frequency, if p 1= p 2(and the sound pressures are in phase at the point in space of the measurement):
(3.28) 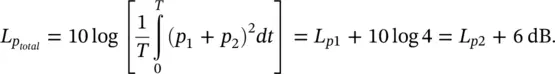
If p 1= p 2= 1 Pa and the two sound pressures are of the same amplitude and frequency and in phase with each other, then the total sound pressure level
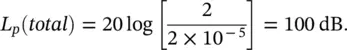
If p 1= p 2= 1 Pa and the two sound pressures are of the same amplitude and frequency, but in opposite phase with each other, then the total sound pressure level
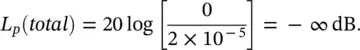
For such a case as in Example 3.2above, for pure tone sounds, instead of 83 dB, the total sound pressure level can range anywhere between 86 dB (for in‐phase sound pressures) and −∞ dB (for out‐of‐phase sound pressures). For the Example 3.3above, the total sound power radiated by the two pure‐tone sources depends on the phasing and separation distance.
Читать дальше

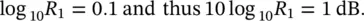
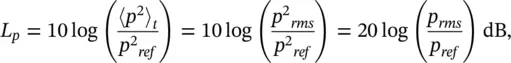

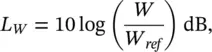

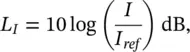
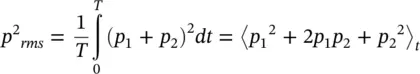
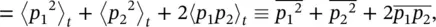
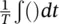 .
.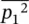 and
and 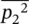 are additive, and the total mean square sound pressure at some point in space, if they are completely independent noise sources, may be determined using Eq. (3.26).
are additive, and the total mean square sound pressure at some point in space, if they are completely independent noise sources, may be determined using Eq. (3.26).