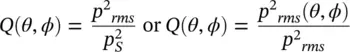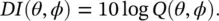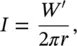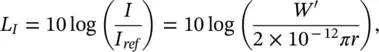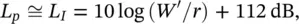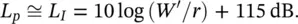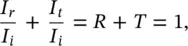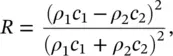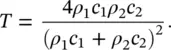(3.53) 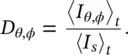
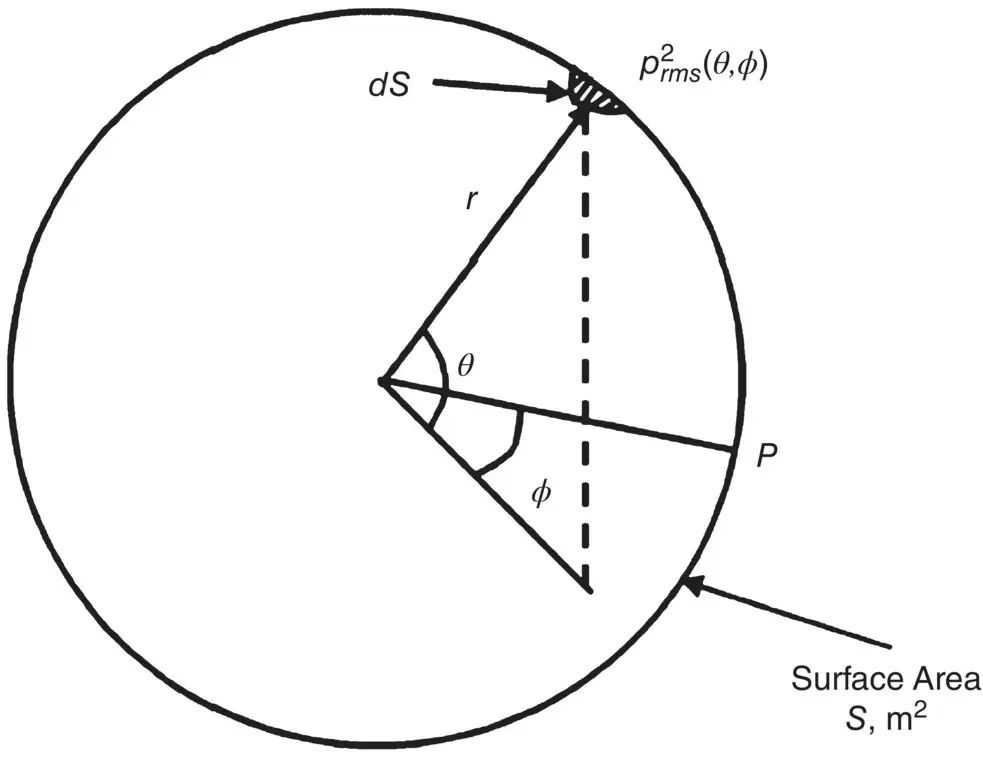
Figure 3.12 Geometry used in derivation of directivity factor.
For a directional source, the mean square sound pressure measured at distance r and angles θ and ϕ is p 2 rms( θ,ϕ ).
In the far field of this source ( r ≫ λ ), then
(3.54) 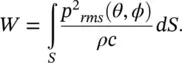
But if the source were omnidirectional of the same power W , then
(3.55) 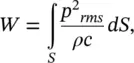
where p 2 rmsis a constant, independent of angles θ and ϕ .
We may therefore write:
(3.56) 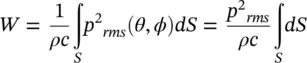
and
(3.57) 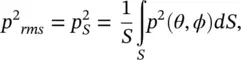
where 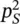 is the space‐averaged mean‐square sound pressure.
is the space‐averaged mean‐square sound pressure.
We define the directivity factor Q as
(3.58) 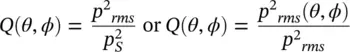
the ratio of the mean‐square sound pressure at distance r to the space‐averaged mean‐square pressure at r , or equivalently the directivity Q may be defined as the ratio of the mean‐square sound pressure at r divided by the mean‐square sound pressure at r for an omnidirectional sound source of the same sound power W , watts.
The directivity index DI is just a logarithmic version of the directivity factor Q . It is expressed in decibels.
A directivity index DI θ,ϕmay be defined, where
(3.59) 
(3.60) 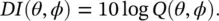
Note if the source power remains the same when it is put on a hard rigid infinite surface Q ( θ , ϕ ) = 2 and DI ( θ , ϕ ) = 3 dB.
1 If a constant‐volume velocity source of sound power level 120 dB (which is equivalent to 1 acoustic watt) radiates to whole space and it has a directivity factor of 12 at 50 m, what is the sound pressure level in that direction?
2 If this constant‐volume velocity source is put very near a hard reflecting floor, what will its sound pressure level be in the same direction?
1 We have that I = 1/4π(50)2 = 1/104 π (W/m2), then But for the directional source Lp(θ, ϕ) = 〈Lp〉S + DI(θ, ϕ), then assuming ρ c = 400 rayls, Lp(θ, ϕ) = 75 + 10 log 12 = 75 + 10 + 10 log 1.2 = 85.8 dB.
2 If the direction is away from the floor, then
Sometimes noise sources are distributed more like idealized line sources . Examples include the sound radiated from a long pipe containing fluid flow or the sound radiated by a stream of vehicles on a highway.
If sound sources are distributed continuously along a straight line and the sources are radiating sound independently, so that the sound power/unit length is W′ watts/metre, then assuming cylindrical spreading (and we are located in the far acoustic field again and ρc = 400 rayls):
(3.61) 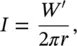
so,
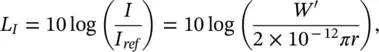
then
(3.62) 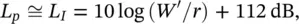
and for half‐space radiation (such as a line source on a hard surface, such as a road)
(3.63) 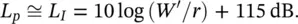
3.11 Reflection, Refraction, Scattering, and Diffraction
For a homogeneous plane sound wave at normal incidence on a fluid medium of different characteristic impedance ρc , both reflected and transmitted waves are formed (see Figure 3.13).
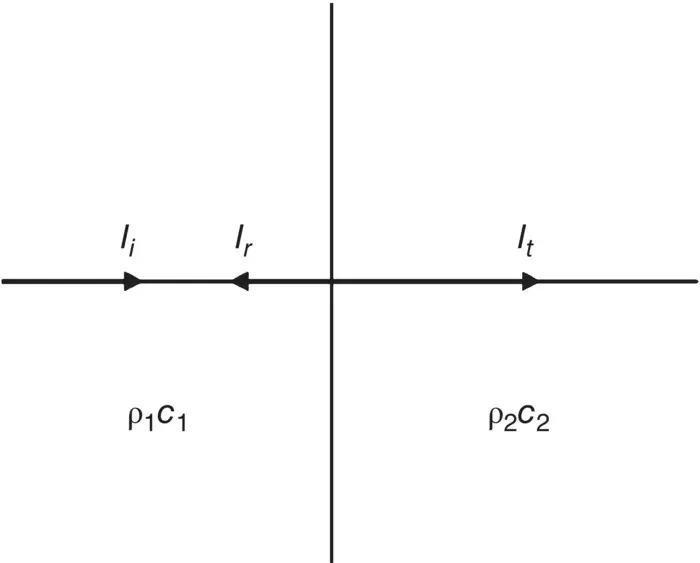
Figure 3.13 Incident intensity I i, reflected intensity I r, and transmitted intensity I tin a homogeneous plane sound wave at normal incidence on a plane boundary between two fluid media of different characteristic impedances.
From energy considerations (provided no losses occur at the boundary) the sum of the reflected intensity I rand transmitted intensity I tequals the incident intensity I i:
(3.64) 
and dividing throughout by I i,
(3.65) 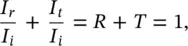
where R is the energy reflection coefficient and T is the transmission coefficient . For plane waves at normal incidence on a plane boundary between two fluids (see Figure 3.13):
(3.66) 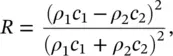
and
(3.67) 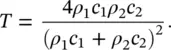
Some interesting facts can be deduced from Eqs. (3.66)and (3.67). Both the reflection and transmission coefficients are independent of the direction of the wave since interchanging ρ 1 c 1and ρ 2 c 2does not affect the values of R and T . For example, for sound waves traveling from air to water or water to air, almost complete reflection occurs, independent of direction; the reflection coefficients are the same and the transmission coefficients are the same for the two different directions.
Читать дальше

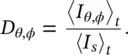

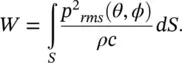
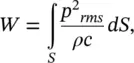
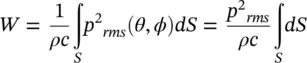
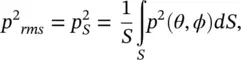
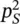 is the space‐averaged mean‐square sound pressure.
is the space‐averaged mean‐square sound pressure.