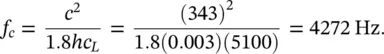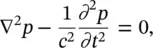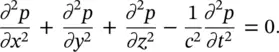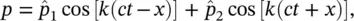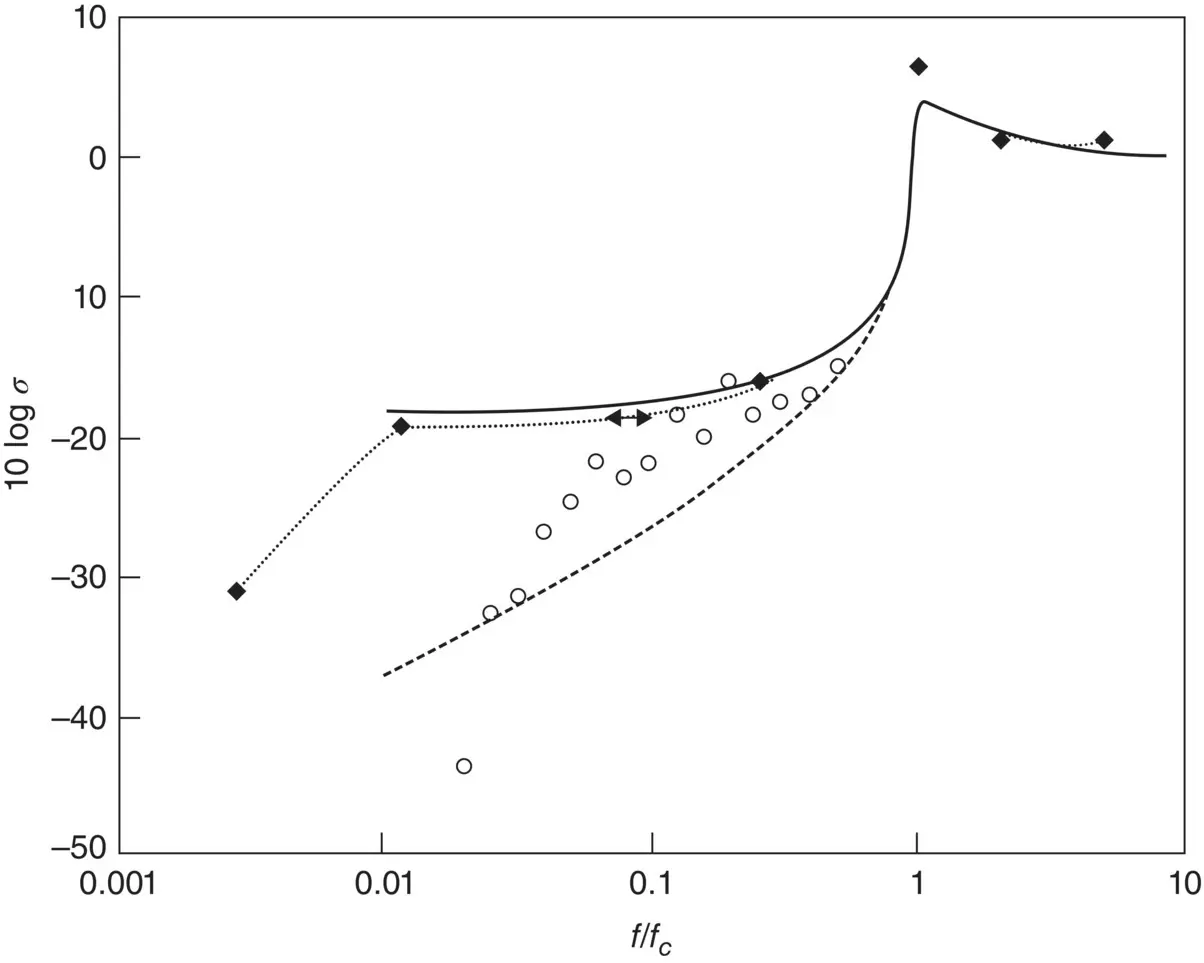
Figure 3.28 Comparison of theoretical and measured radiation ratios σ for a mechanically excited, simply-supported thin steel plate (300 × 300 × 1.22 mm). (—) Theory (simply-supported), (‐ ‐ ‐) theory (clamped edges), (⋅⋅⋅⋅⋅⋅⋅) theory [28], and (○) measured [29] (see [30]).
Determine the critical frequency for a 3 mm thick steel plate.
The longitudinal wave speed in aluminum is c L= 5100 m/s. Now, replacing κ = h /(12) 1/2in Eq. (3.85)yields
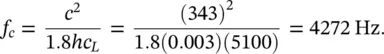
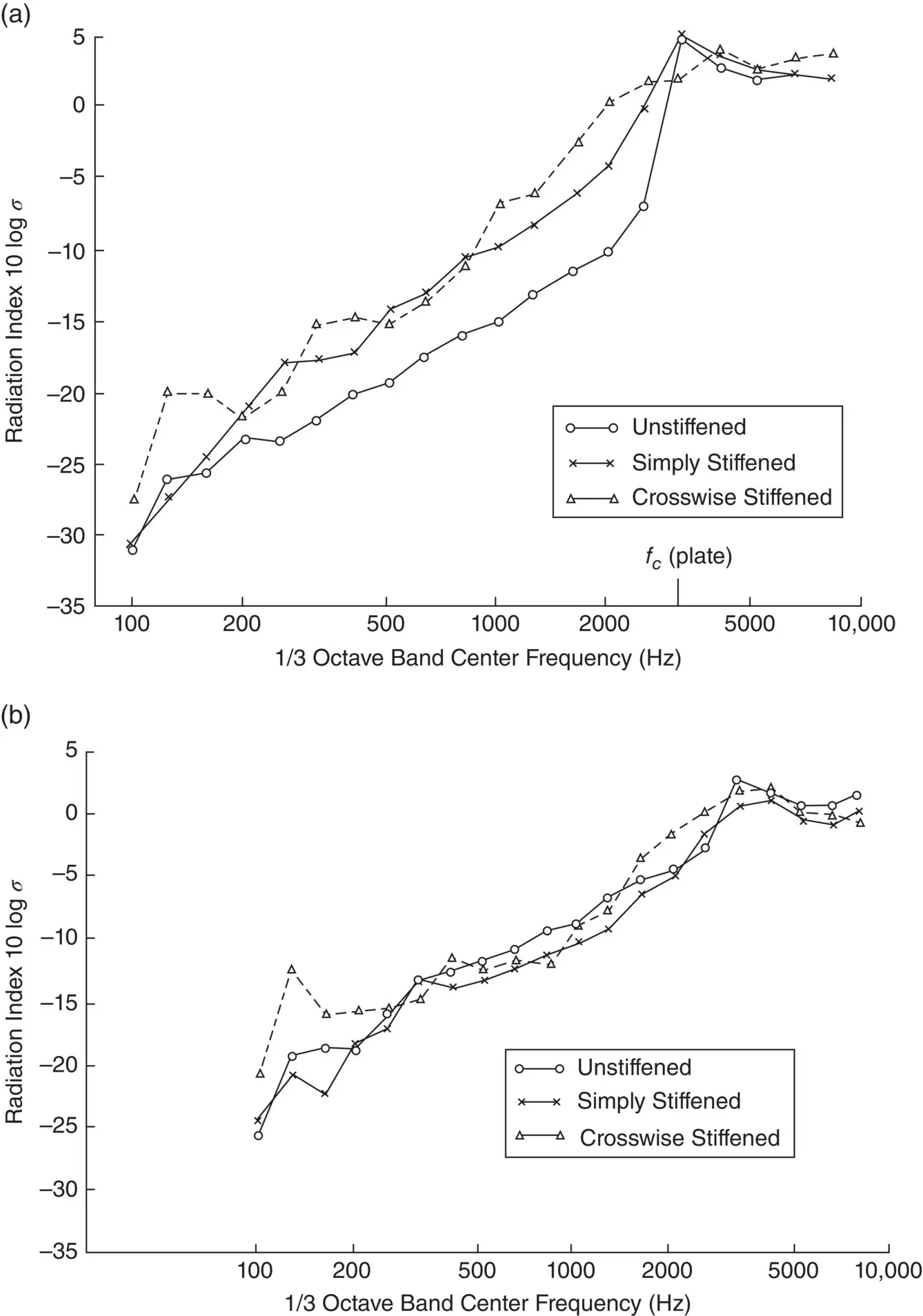
Figure 3.29 Measured radiation ratios of unstiffened and stiffened plates for (a) point mechanical excitation and (b) diffuse sound field excitation.
( Source: Reproduced from Ref. [31] with permission. See [30].)
Sound transmission through structures is discussed in Chapter 12of this book and chapters 66, 76, and 77 of the Handbook of Acoustics [1].
Figure 3.29a and b show the logarithmic value of the radiation efficiency 10log σ plotted against frequency for stiffened and unstiffened plates. See Ref. [27] for further discussion on the radiation efficiency σ rad, which is also known as radiation ratio.
Standing‐wave phenomena are observed in many situations in acoustics and the vibration of strings and elastic structures. Thus they are of interest with almost all musical instruments (both wind and stringed) (see Part XIV in the Encyclopedia of Acoustics [19]); in architectural spaces such as auditoria and reverberation rooms; in volumes such as automobile and aircraft cabins; and in numerous cases of vibrating structures, from tuning forks, xylophone bars, bells and cymbals to windows, wall panels, and innumerable other engineering systems including aircraft, vehicle, and ship structural members. With each standing wave is associated a mode shape (or shape of vibration) and an eigen (or natural) frequency. Some of these systems can be idealized as simple one‐, two‐, or three‐dimensional systems. For example, with a simple wind instrument such as a flute, Eq. (3.1)together with the appropriate spatial boundary conditions can be used to predict the predominant frequency of the sound produced. Similarly, the vibration of a string on a violin can be predicted with an equation identical to Eq. (3.1)but with the variable p replaced by the lateral string displacement. With such a string, solutions can be obtained for the fundamental and higher natural frequencies (overtones) and the associated standing wave mode shapes (which are normally sine shapes). In such a case for a string with fixed ends, the so‐called overtones are just integer multiples (2, 3, 4, 5, …) of the fundamental frequency.
The standing wave with the flute and string can be considered mathematically to be composed of two waves of equal amplitude traveling in opposite directions. Consider the case of a lateral wave on a string under tension. If we create a wave at one end, it will travel forward to the other end. If this end is fixed, it will be reflected. The original (incident) and reflected waves interact (and if the reflection is equal in strength) a perfect standing wave will be created. In Figure 3.30we show three different frequency waves that have interacted to cause standing waves of different frequencies on the string under tension. A similar situation can be conceived to exist for one‐dimensional sound waves in a tube or duct. If the tube has two hard ends, we can create similar standing one‐dimensional sound waves in the tube at different frequencies. In a tube, the regions of high sound pressure normally occur at the hard ends of the tube, as shown in Figure 3.31. See Refs. [14, 32, 33].
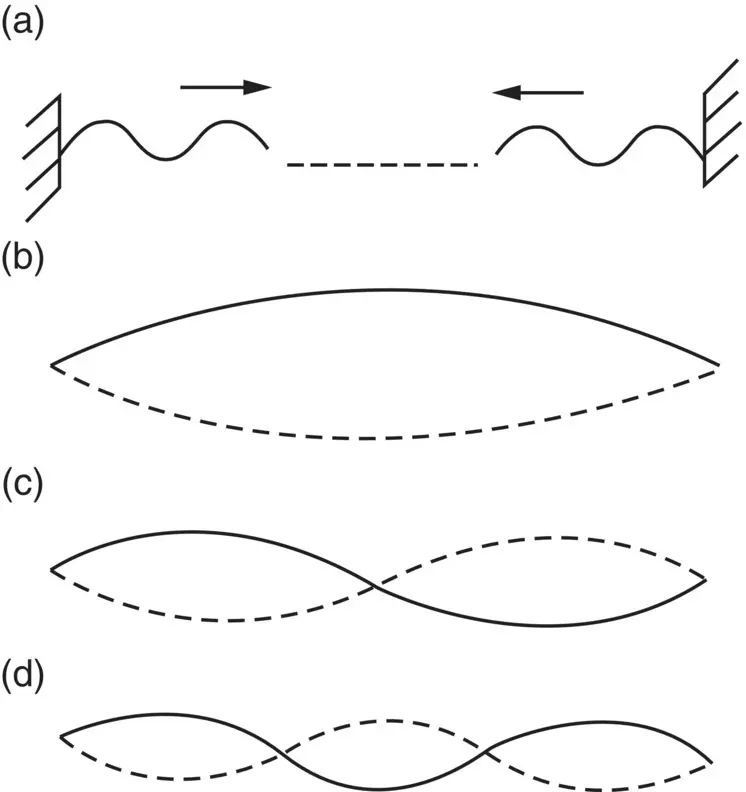
Figure 3.30 Waves on a string: (a) Two opposite and equal traveling waves on a string resulting in standing waves, (b) first mode, n = 1, (c) second mode, n = 2, and (d) third mode, n = 3.
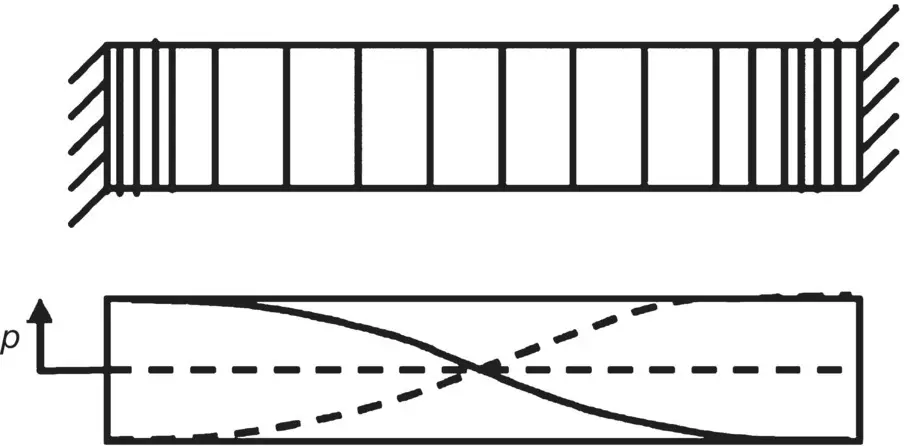
Figure 3.31 Sound waves in a tube. First mode standing wave for sound pressure in a tube. This mode is called the fundamental and occurs at the fundamental frequency.
A similar situation occurs for bending waves on bars, but because the equation of motion is different (dispersive), the higher natural frequencies are not related by simple integers. However, for the case of a beam with simply supported ends, the higher natural frequencies are given by 2 2, 3 2, 4 2, 5 2, … , or 4, 9, 16, 25 times the fundamental frequency, …, and the mode shapes are sine shapes again.
The standing waves on two‐dimensional systems (such as bending vibrations of plates) may be considered mathematically to be composed of four opposite traveling waves. For simply supported rectangular plates the mode shapes are sine shapes in each direction. For three‐dimensional systems such as the air volumes of rectangular rooms, the standing waves may be considered to be made up of eight traveling waves. For a hard‐walled room, the sound pressure has a cosine mode shape with the maximum pressure at the walls, and the particle velocity has a sine mode shape with zero normal particle velocity at the walls. See chapter 6 in the Handbook of Acoustics [1] for the natural frequencies and mode shapes for a large number of acoustical and structural systems.
For a three‐dimensional room, normally there are standing waves in three directions with sound pressure maxima at the hard walls.
To understand the sound propagation in a room, it is best to use the three‐dimensional wave equation in Cartesian coordinates:
(3.86) 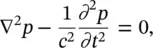
or
(3.87) 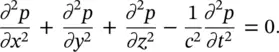
This equation can have solutions that are “random” in time or are for the special case of a pure‐tone, “simple harmonic.”
The simple harmonic solution is of considerable interest to us because we find that in rooms there are solutions only at certain frequencies. It may be of some importance now to mention both the sinusoidal solution and the equivalent solution using complex notation that is very frequently used in acoustics and vibration theory.
For a one‐dimensional wave, the simple harmonic solution to the wave equation is
(3.88) 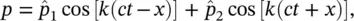
Читать дальше