Alfonso Cabanzo - Lógica básica

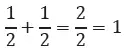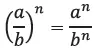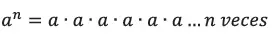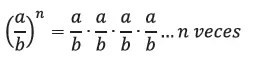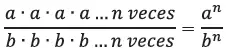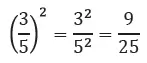
Fuente: elaboración propia.

Sin duda, fue un descubrimiento grandioso el de este físico griego: concluir esto solo mediante razonamientos y observaciones. Pero la argumentación no está destinada únicamente a los grandes matemáticos y científicos: en la vida diaria la usamos. El estudiante que dice: “siempre que el profesor viene, deja su carro en el parqueadero, y como hoy no está su auto, no vino” da un argumento que trata de probar la verdad de la conclusión a partir de las premisas. La lógica nos dirá que el argumento anterior es válido: si “siempre que el profesor viene, deja su carro en el parqueadero” es verdadera y, además, es verdadero que “no está su auto”, tendremos que aceptar la oración “el profesor no vino”. Quizás, nos diga también que la primera es falsa, lo que hace al razonamiento poco sólido. En particular, esta ciencia se centra en la forma y no tanto en el contenido de los razonamientos. De ahí su nombre de lógica formal. No obstante, esta afirmación es algo inexacta: cuando hablamos de verdad o falsedad de las oraciones, nos centramos en su significado y, por ello, también consideramos su contenido, aunque de la manera más general posible. Esta oposición ha sido crucial en el desarrollo científico, pero no pocas veces ha causado tantos enredos, en particular, porque se suele olvidar: nos centramos muchas veces en la forma, tanto que el contenido se pierde, lo que dificulta la comprensión de las demostraciones y las argumentaciones. La matemática nos da el mejor ejemplo de ello.

Veamos la siguiente ecuación:

(a + b)2 = a2 + 2ab + b2

Esta fórmula suele expresarnos una forma, pero pocas veces el profesor se toma la molestia de recalcarle al alumno qué significa. Por ejemplo, no se hace ninguna asociación entre la multiplicación aritmética y el cálculo del área de una figura geométrica. Con ello, se olvida lo siguiente: el cuadrado de un número a2 es simplemente el cuadrado cuyo lado mide a:

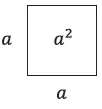
Según esto, a2 es una manera general, abstracta, de decir “el cuadrado cuya área se calcula multiplicando la magnitud a por sí misma”.

Por supuesto, (a + b)2 es una forma abreviada de decir: “el cuadrado cuyo lado es a + b”. La ecuación mencionada dice simplemente: “el cuadrado cuyo lado es a + b es el resultado de tomar un cuadrado cuyo lado es a, sumado a dos rectángulos cuyos lados son a y b sumados a otro cuadrado cuyo lado es b”. La representación gráfica no solo nos explica esta ecuación, sino que también se convierte en una especie de demostración intuitiva o gráfica:

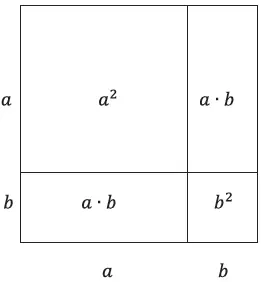
En resumen, a2 es decir: “un cuadrado cuya área se calcula así: a. a". Este olvido hace que la enseñanza de las matemáticas sea ardua: primero, porque se deja atrás su aplicación práctica. Segundo, porque esta omisión nos obliga a centrarnos en los símbolos, aparentemente carentes de todo sentido, haciendo difícil su manipulación. De ahí que la disciplina se convierte en una técnica de manejo de garabatos absurdos. Pero, la abstracción en sí no es mala: al hablar de signos con muchas interpretaciones, podemos generalizar y aplicar los resultados a campos más amplios. Es así como podemos calcular volúmenes, como cubos: a3 sería la representación de una figura tridimensional. Limitaciones obvias nos impiden presentarlo tal cual, pero podemos intentarlo:

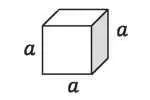
La representación de (a + b) = a3 + 3a2b + 3ab2 + a3 sería ya más engorrosa. El lector puede tratar de demostrarla en tres dimensiones, haciendo las figuras con cartón. Lo mismo sucede con otros principios matemáticos simples:

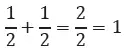
Esta suma simplemente representa la operación de dividir una unidad en dos mitades para luego volverlas a pegar:

Unidad: 1

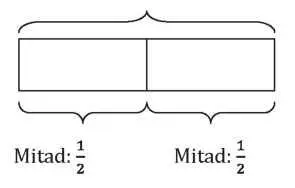
Podemos abstraer aún más y demostrar:

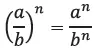
Nótese que no alcanzamos a imaginarnos una figura geométrica como An. Nuestro intelecto nos permite, no obstante, comprender la definición:

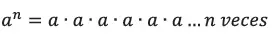
A partir de esta definición sabemos que:

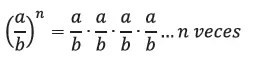
Como sabemos, multiplicar fraccionarios, tenemos que:

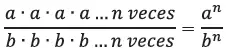
Sin capacidad de abstracción, la prueba no se puede entender. No hay intuición que nos permita aprehenderla en su totalidad desde la perspectiva geométrica. Y este grado de generalidad nos permite aplicar este conocimiento abstracto posteriormente a muchos casos particulares. Sabemos gracias a esta regla demostrada que:

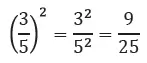
Esto gracias a que reemplazamos en la regla general la letra a por el 3, la letra b por el 5, y la letra n por el 2. El conocimiento de los principios generales nos ayuda a solucionar casos particulares.

La lógica formal parte igualmente de lo concreto, el lenguaje cotidiano y sus argumentos, para ir haciéndose cada vez más abstracta. Nos suministra leyes y, posteriormente, estas leyes nos ayudarán en los casos particulares. Su estudio busca generar esa capacidad de abstracción de ver el esquema abstracto, para poder aplicarlo al caso concreto. Este procedimiento se suele llamar deducción. definido un poco de manera más clara, para diferenciarlo de lo que en lógica se llama deducción formal.

La definición tradicional afirma que la deducción es el paso de lo general a lo particular. Y es cierta, pero incompleta. También es el paso de premisas que, si son verdaderas, prueban concluyente mente la conclusión. El ejemplo típico es el siguiente: “Todas las bolas de esta bolsa son blancas. Estas bolas estaban en esta bolsa, por tanto, son blancas” (Eco, 1991). Si todas las bolas de la bolsa son blancas, no hay posibilidad de que las bolas tomadas de allí sean de otro color; si sacamos una bola negra, necesariamente tendríamos que negar alguna de las premisas: estábamos equivocados, no todas las bolas eran blancas, o bien, la bola negra no proviene de la bolsa: se nos coló de alguna manera. En general, la matemática es una disciplina que utiliza esta técnica de la deducción de principio a fin.