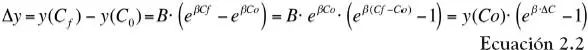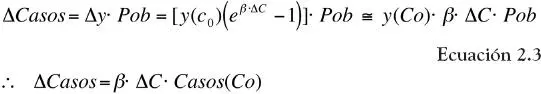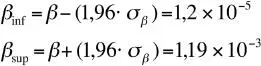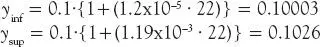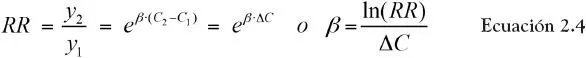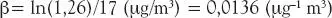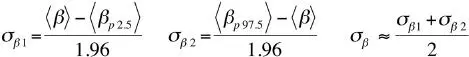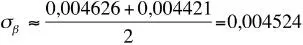Héctor Jorquera González - Introducción a la contaminación atmosférica

En este capítulo nos enfocaremos exclusivamente al caso de la epidemiología ambiental, dejando de lados los estudios clínicos (como toxicología o salud ocupacional, por ejemplo) que poseen su propia metodología de análisis.

2.3.1 El modelo de Poisson (efectos de corto plazo)

Para mostrar cómo se analizan los datos, vamos a considerar la tasa de incidencia de un efecto genérico y la vamos a denominar y. La variable independiente va a ser la concentración de material particulado, denominado C , aunque podría ser cualquier otro contaminante o grupo de ellos.

Los estudios epidemiológicos han usado diversas expresiones para relacionar y con C . Sin embargo, el modelo estándar que se utiliza en la actualidad es la regresión tipo Poisson, puesto que la variable modelada es una cantidad discreta (número de casos diarios, por ejemplo), la que se asume distribuida de acuerdo a un proceso estocástico, no estacionario, del tipo Poisson. Luego la forma de la relación C-R es la siguiente:

Donde el parámetro B sería la tasa de incidencia del efecto estudiado cuando la concentración del contaminante fuese cero (claramente esto es una extrapolación); el parámetro β es el coeficiente de la relación C-R, el cual se estima mediante técnicas estadísticas especiales (ver siguiente sección).

Considerando que existen otras variables (además del contaminante) que afectan a las tasas de incidencia, se puede considerar que el parámetro B las incluye; sin embargo, el parámetro B no aparece explícitamente cuando se evalúan cambios en la tasa de incidencia. En efecto, a partir de la relación C-R, la relación entre cambios en niveles de concentración en el ambiente y cambios en tasas de incidencia se puede escribir en la siguiente forma:

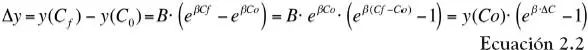
Donde y (C 0) es la tasa de incidencia de referencia 14para una concentración de referencia C 0. Luego, se puede estimar el cambio en el número de efectos adversos a la salud mediante la expresión

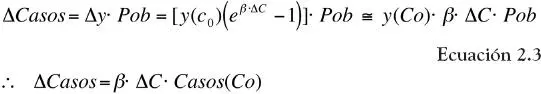
Donde Pob es la población expuesta; aquí se nota que si baja la contaminación, el valor de Δ Casos es negativo, lo que es lógico. La aproximación lineal en la ecuación anterior (ampliamente utilizada en la literatura de estimación de beneficios) se justifica debido a que β·ΔMP << 1,0 para las funciones C-R típicas que se han encontrado en los estudios epidemiológicos.

Ejemplo 2.1

Ostro y otros (1991) han reportado un coeficiente β = 0,0006 para MP 2.5en el caso de incidencia de ataques de asma en la población, con un error estándar de 0,0003. Por lo tanto, las cotas de dicho coeficiente, para un intervalo de 95% de confianza, son:

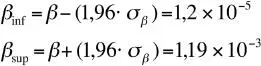
Esto significa que el efecto es significativo al 95% de confianza, ya que el intervalo respectivo no contiene el valor 0. A partir de esto es posible estimar intervalos de confianza para este efecto en salud.

Si consideramos una población de 1,6 millones de personas menores de 15 años en Santiago, de los cuales 10% tiene asma 15, un nivel de MP 2.5de 27 (μg/m 3), una tasa de incidencia base de 10.000 ataques por cada 100.000 habitantes 16, y que el nivel de buena calidad del aire sería de MP 2.5=5 (μg/m 3), entonces tendríamos que la tasa de incidencia para Santiago posee el siguiente intervalo de confianza:

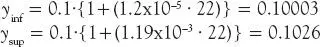
Es decir, esperaríamos que con los actuales niveles de contaminación por material particulado, el exceso de ataques anuales de asma (Δ y en ecuación 2.2) se estima entre 3 y 260 por cada 100.000 habitantes, o bien entre 5 y 416 ataques adicionales al año para la población asmática en Santiago, con 95% de confianza. Note el gran intervalo de valores para este efecto en particular, el cual es típico de los estudios epidemiológicos.

Considerar además que este resultado se ha obtenido extrapolando los resultados del estudio de Ostro y otros (1991) a la ciudad de Santiago, lo cual no necesariamente es la mejor elección. Sería deseable contar con estimaciones locales de la magnitud de este efecto en la población, pero en este caso no existe tal estudio. En ausencia de estudios locales, es la mejor estimación que se puede hacer por el momento.

2.3.2 Riesgo relativo para el modelo estándar

Se define el riesgo relativo ( RR ) asociado a un cambio en la calidad del aire Δ C como el cociente entre la tasa de incidencia del efecto en salud y un valor de referencia, luego:

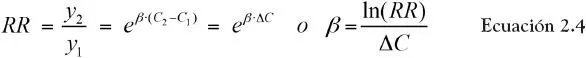
Lo cual define la relación entre el riesgo relativo y el coeficiente de la relación C-R para el modelo estándar dado por la ecuación 2.1. Ambos indicadores se entregan como resultado de los análisis de epidemiología ambiental; por ejemplo, al incrementarse en 10 (μg/m 3) la concentración ambiental de MP 2.5, el riesgo de mortalidad total en la población es de 1,01, lo que equivale a 1% de incremento en la tasa de mortalidad total de corto plazo 17.

Ejemplo 2.2

En el caso del estudio de cohorte de Dockery y otros (1993), se encontró RR = 1,26 cuando se compararon las tasas de mortalidad en Steubenville (Ohio) y Portage (Wisconsin), siendo las concentraciones ambientales de MP 2.5de 29 y 12 (μg/m 3), respectivamente, lo que produce el estimador

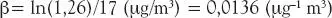
Los coeficientes asociados con las cotas superior e inferior de β (usualmente son los percentiles 2,5 y 97,5) se pueden estimar usando los valores reportados para los intervalos de confianza de riesgo relativo. Debido a errores de redondeo de los datos publicados, los errores estándar calculados con ambos extremos del intervalo de confianza no van a coincidir, de modo que se hace la siguiente aproximación:

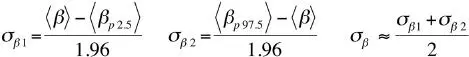
Donde el símbolo <...> indica que se ha estimado el error estándar usando el valor respectivo de riesgo relativo de acuerdo a la ecuación 2.4. En el mismo estudio ya citado, se encontró para el riesgo relativo el intervalo de confianza [1,08, 1,46], de modo que se estima que:

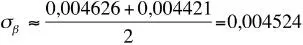
Y con esto se puede calcular además el valor t para β, el cual en este caso toma el valor t β= 0,0136/0,00452 = 3,0, lo que corresponde a un parámetro muy significativo.