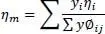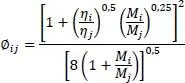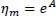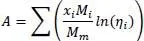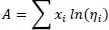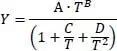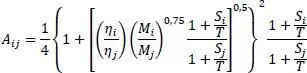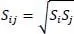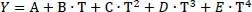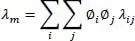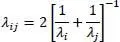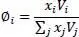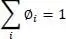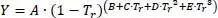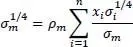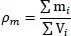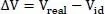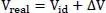Wolfgang Schmidt - Berechnung von Stoffdaten und Phasengleichgewichten mit Excel-VBA

Abb. 2.16. Flüssigviskosität von N-Oktan nach der DIPPR-Gleichung 101 in CHEMCAD

Die ideale Mischungsviskosität für Gase wird wie folgt berechnet:

(2.27)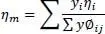

Mit η mder Mischungsviskosität, y idem Dampfmolanteil, η ider Gasviskosität des Reinstoffes.

Weiter gilt

(2.28)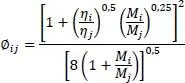

Darin ist M das Molgewicht.

Die ideale Mischungsviskosität für Flüssigkeiten wird wie folgt berechnet:

(2.29)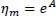

Mit

(2.30)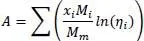

Darin ist x der Molanteil und M das Molgewicht.

Wenn das gesamte Molgewicht aller Komponenten geringer als 2000 ist, gilt

(2.31)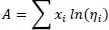

Die Gaswärmeleitfähigkeit wird nach der DIPPR-Formel 102 berechnet

(2.32)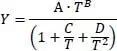

Für N-Oktan gelten die in Abb. 2.17aufgeführten Daten.

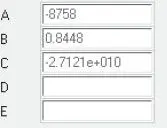
Abb. 2.17. Koeffizienten von N-Oktan für DIPPR-Gleichung 102

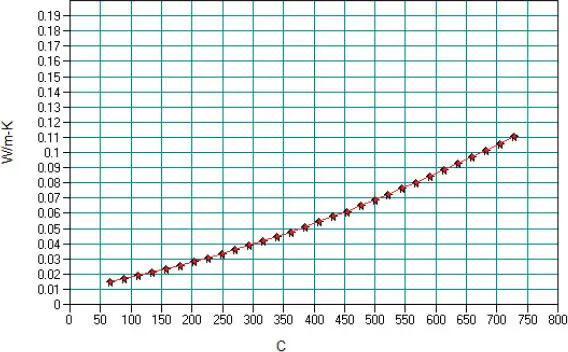
Abb. 2.18.Gaswärmeleitfähigkeit von N-Oktan nach der DIPPR-Gleichung 102 in CHEMCAD

Die Mischungswärmeleitfähigkeit λ mfür Gase wird wie folgt berechnet:

(2.33)

Darin ist λ mdie Wärmeleitfähigkeit der Mischung, λ idie Wärmeleitfähigkeit des Reinstoffes, n die laufende Nummer der Komponente und y ibzw. y jder Dampfmolanteile der Komponente i bzw. j.

Weiter gilt

(2.34)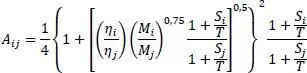

Darin ist S die Sutherland Konstante S = 1,5 * T b. T bist der Siedepunkt.

(2.35)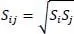

Mit η, der Viskosität, M dem Molgewicht und T der Temperatur.

Die ideale Wärmeleitfähigkeit für Flüssigkeiten wird nach der DIPPR-Formel 100 berechnet

(2.36)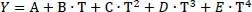

Die Mischungswärmeleitfähigkeit λ mfür Flüssigkeiten wird wie folgt berechnet:

(2.37)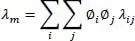

(2.38)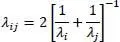

(2.39)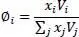

(2.40)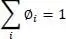

Darin ist φ iund φ jder Volumenanteil, λ iund λ jdie Wärmeleitfähigkeit des Reinstoffes, V iund V jdas Molvolumen des Reinstoffes und x ibzw. x jder Molanteil.

Die Oberflächenspannung σ wird mit der DIPPR-Funktion 106 berechnet.

(2.41)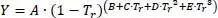

Die Mischungsoberflächenspannung einer Flüssigkeit wird wie folgt berechnet:

(2.42)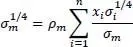

Diese Mischungsregeln haben sich in der Praxis gut bewährt und gelten sowohl für binäre wie auch Mehrkomponentengemische.

Die Flüssigdichte von idealen Gemischen wird im Allgemeinen nach einer linearen Mischungsregel berechnet, diese lautet:

(2.43)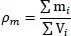

Darin ist m die Masse und V das Volumen. Man unterscheidet zwischen idealen und realen Mischungen. Bei idealen Mischungen treten keine Volumeneffekte auf, während diese bei realen Mischungen mehr oder weniger stark zu finden sind. Die Voraussetzung der idealen Addition der Volumina ist offensichtlich bei gleichgroßen Molekülen gegeben. Daher ist die ideale Dichteformel eine Näherung, die es gilt zu verbessern.

Ein vielfach publiziertes Beispiel ist das Ethanol-Wasser-Gemisch (Gmehling et al., 1992, S. 80) und (Lüdecke et al., 2000, S. 445). Mischt man 500 cm 3Ethanol (58,55 cm 3/mol) = 8,54 mol mit 500 cm 3Wasser (18,06 cm 3/mol) = 27,68 mol bei 25 °C, so sollte das Mischungsvolumen 1000 cm 3betragen. Tatsächlich aber beträgt es nur 973,5 cm 3, d.h. 26,44 cm 3weniger.

Der Ansatz zur Berechnung dieses Effektes lautet:

(2.44)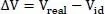

(2.45)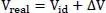

Definiert man die Größen auf ein Mol, so gilt ΔV = n * Δv. Darin ist n die Molmenge und Δv das spezifische molare Volumen. In diesem Beispiel gilt n = n 1+ n 2= 8,54 mol + 27,68 mol = 36,22 mol. Da ΔV = 26,44 cm 3ist, wird Δv = -0,73 cm 3/mol.

Nun gilt dieser Wert aber nur für die vorliegende Mischung. Ein universelles Modell, welches für alle binären Flüssiggemische gilt, ist nicht bekannt. Daher wird der Porter-Ansatz gewählt.

Dieser Ansatz ist bekannt als der einfachste Ansatz zur Beschreibung der Exzessenthalpie g E=Ax 1x 2in einer binären Mischung. Führt man eine analoge Betrachtung zum Volumeneffekt als Exzessvolumen durch, so liegt es nahe, den Ansatz