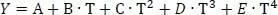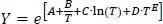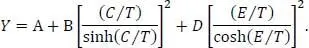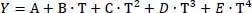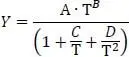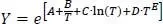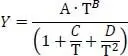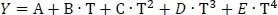Wolfgang Schmidt - Berechnung von Stoffdaten und Phasengleichgewichten mit Excel-VBA

Diese Funktion benötigt nur die Parameter A bis D. Diese 4 Parameter liegen für Ethanol vor. Der untere Gültigkeitswert bei T u= 159,05 K beträgt 19,4128 kmol/m 3, bei T 0= 513,92 K beträgt er hingegen 5,96518 kmol/m 3.

Für die Feststoffdichte gilt die DIPPR-Formel Nr. 100. Diese lautet

(1.31)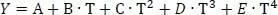

In dieser Funktion genügt im Minimalfall sogar nur 1 Parameter. Und tatsächlich liegt auch nur ein einziger Parameter, nämlich 22,9 kmol/m 3, für Ethanol vor. D.h. die Dichte von festem Ethanol ist also nur mit 22,9 kmol/m 3in der Datenbank enthalten. Vermutlich liegen keine weiteren Messungen vor.

Im nächsten Screenshot geht es um den Dampfdruck und die Verdampfungsenthalpie ( Abb. 1.30).

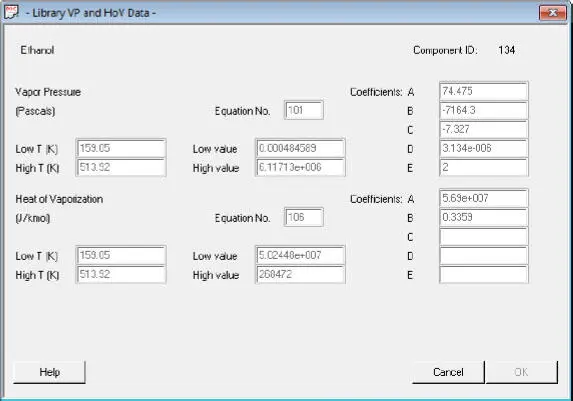
Abb. 1.30. Dampfdruck (101) und Verdampfungsenthalpie (106) nach DIPPR

Der Dampfdruck wird nach der DIPPR-Funktion 102 berechnet. Diese lautet

(1.32)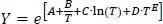

Die Funktion entspricht der Clausius-Clapeyron-Formel und einer empirischen Erweiterung mit den Parametern C, D und E.

Die Verdampfungsenthalpie wird nach der DIPPR-Funktion 106 berechnet. Diese lautet

(1.33)

Die spezifischen Wärmekapazitäten Cp werden nach den DIPPR-Funktionen 107, und 100 berechnet ( Abb. 1.31).

Abb. 1.31. Spezifische Wärmekapazitäten fest (107), flüssig (100) und gasförmig (100)

Die DIPPR-Funktion 107 lautet

(1.34)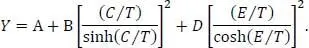

Früher verwandte man für Cp nur die Polynomfunktion. Diese versagte jedoch u.a. bei Wasserstoff und Helium, da die spezifische Wärmekapazität (Cp-Wert) über einen weiten Temperaturbereich nahezu konstant bleibt. Die Funktion 107 kann diese Eigenschaft erheblich besser darstellen.

Die Funktionen 100 lauten wie oben bereits genannt

(1.35)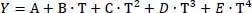

Auch hier ist bei den Polynomansätzen (DIPPR-Formel 100) zu beobachten, dass die Koeffizienten jeweils etwa um den Faktor 1000 kleiner werden, um die Gefahr der Polynomwelligkeit zu vermeiden.

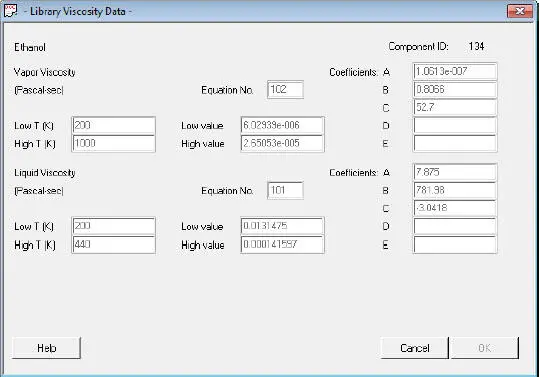
Abb. 1.32. DIPPR-Funktion für Gasviskosität (102) und Flüssigviskosität (101)

Im Screenshot ( Abb. 1.32) kann die Gasviskosität aus der DIPPR-Funktion 102 berechnet werden

(1.36)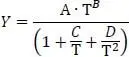

Die Funktion 101 für die Flüssigviskosität lautet

(1.37)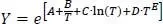

Sie ist damit identisch mit der Funktion für den Dampfdruck.

Im nächsten Screenshot ( Abb. 1.33) finden wir die DIPPR-Funktionen für die Gas- und Flüssigwärmeleitfähigkeit sowie die Oberflächenspannung.

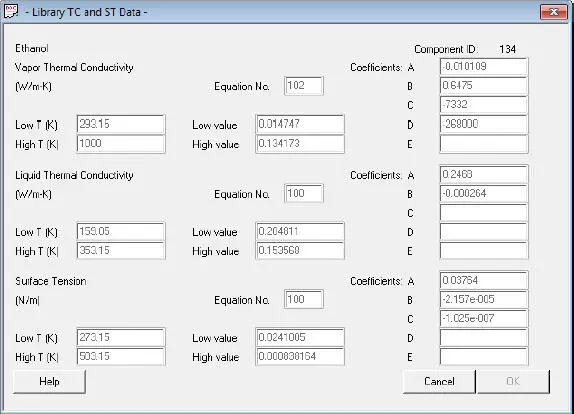
Abb. 1.33. Gaswärmeleitfähigkeit, Flüssigwärmeleitfähigkeit, Oberflächenspannung

Die DIPPR-Funktion für die Gaswärmeleitfähigkeit hat die Nr. 102 und lautet

(1.38)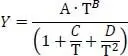

Die DIPPR-Funktionen für die Flüssigwärmeleitfähigkeit sowie die Oberflächenspannung haben die Nr. 101 und lauten

(1.39)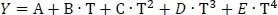

Dies sind die DIPPR-Funktionen wie sie in CHEMCAD zum Einsatz kommen.

Der Prozess zur Gewinnung dieser Funktionen und Parameter bei DIPPR ist komplex und aufwendig. Es beginnt mit einer Datenrecherche in diversen englischsprachigen Publikationen. Die gewonnenen Messdaten werden mithilfe von statistischen Methoden verglichen und geprüft und daraus durch Regression die Parameter ermittelt. DIPPR führt selber keine Messungen durch. Wenn man den Zugang zur DIPPR-Datenbank erwirbt, erhält man genaue Informationen über die Datenquellen.

Mit dem Freeware-Tool DWSIM, welches von Daniel, einem brasilianischen Ingenieur der Minaralöltechnik erstellt und von diversen Mitarbeitern weltweit unterstützt wird, stehen umfangreiche Excel-Funktionen zur Verfügung. Diese werden allerdings über ein spezielles Verfahren direkt nach Excel geladen. Man findet sie unter PVFFLASH.

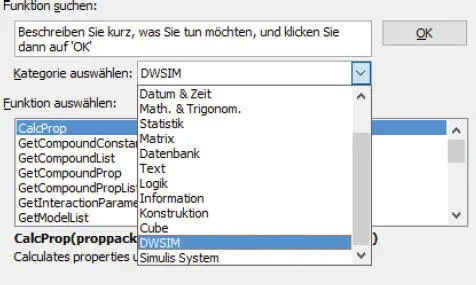
Abb. 1.34. Funktion einfügen

Beim Auswählen der Excelfunktion unter Abb. 1.34ist zunächst die Kategorie DWSIM zu wählen. Dann werden alle DWSIM-Funktionen angezeigt. In dieser Excelberechnung wird die o.g. Funktion PVFFLASH ( Abb. 1.35) benötigt.

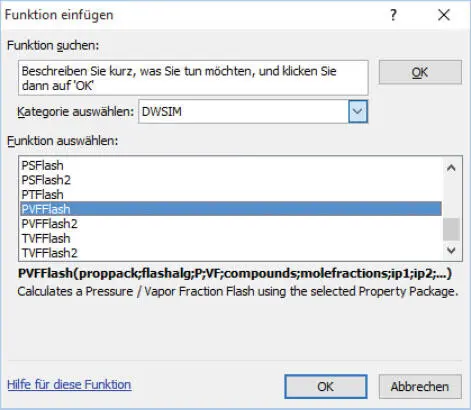
Abb. 1.35. Auswahl PVFFlash

In D8:F11 findet man ( Abb. 1.36)

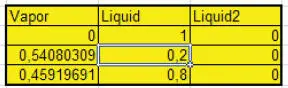
Abb. 1.36. Zellen D8 bis F11

mit der Funktion ( Abb. 1.37)

Abb. 1.37. Funktion PVFFlash

in E10:F11. Die geschweifte Klammer ist nötig, da das Ergebnis dieser Funktion eine Tabelle (Matrix) ist. Wie in der runden Klammer selbst zu sehen und allgemein bekannt ist, braucht diese Funktion wie jede andere auch Parameter (vgl. Abb. 1.38).