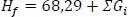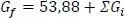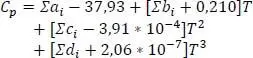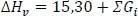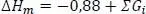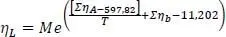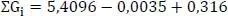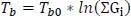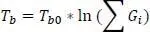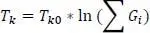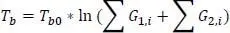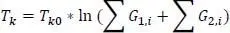Wolfgang Schmidt - Berechnung von Stoffdaten und Phasengleichgewichten mit Excel-VBA

Standardbildungsenthalpie Hf

(1.14)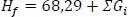

Gibbs’sche Standardbildungsenergie Gf

(1.15)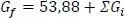

Spezifische Wärmekapazität des idealen Gases Cp

(1.16)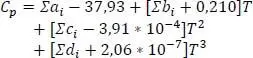

Standardverdampfungsenthalpie ΔHv

(1.17)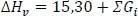

Standardschmelzenthalpie ΔHm

(1.18)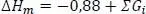

Dynamische Viskosität der Flüssigkeit ηL

(1.19)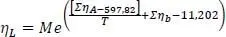

Darin ist M das Molgewicht, e die e-Funktion.

Neben den hier aufgeführten Stoffdaten der Joback-Methode lassen sich in CHEMCAD weitere Stoffdaten wie Azentrischer Faktor ω, Liquid Volume Constant, Specific Gravity, Solubility Parameter, Watson Factor mit der Joback-Methode berechnen. Eine entsprechende Dokumentation ist bei www.chemstations.comerhältlich.

Die Stärke der Joback-Methode besteht in der einfachen und der sehr flexiblen Verwendung. Ihre Schwäche ist die, dass die genaue Molekülstruktur und damit Wechselwirkungen der gewählten Gruppen mit Nachbargruppen nicht berücksichtigt werden. Dies ist allerdings die Schwäche vieler Inkrementmethoden, was offensichtlich zwei Gründe hat. Einerseits besagen die Inkremente ohnehin nichts über Wechselwirkungen untereinander, andererseits auch nichts über ihre Position in einem Molekül. Wie bereits dargestellt, bestehen z.B. zwischen einem CH3-Inkrement und dem OH-Inkrement andere Wechselwirkungen als zwischen dem CH3- und dem CH 2-Inkrement. Während für viele einfache Moleküle die Molekülstruktur aus den Inkrementen eindeutig hervorgeht, ist das bei größeren Molekülen nicht der Fall, z.B. bei Isomeren. So stellt 2 CH 3- eindeutig Ethylen dar. Aber 4 CH 3-, 2 CH 2- und 2 CH- ergeben 3 Isomere, nämlich 2,3-, 2,4- und 2,5-Dimethylhexan (DMH). Deren Siedepunkt würde mit Joback für alle 3 Isomere Tb = 551,52 K ergeben (Ex_xls), (ifp15). Tatsächlich betragen die Siedetemperaturen für 2,3-DMH T b= 563,5 K, für 2,4-DMH T b= 553,6 K und für 2,5-DMH T b= 550 K.

Bei diesem Molekül kann man annehmen, dass Wechselwirkungen kaum die Ursache für die unterschiedlichen Siedetemperaturen sein können, sondern eher die Positionen. Warum das so ist, ist wenig erforscht. Wir können also nur empirisch vorgehen und die speziellen Positionen herausfinden und ihnen Joback-Werte zuordnen.

In der Literatur sind neben der Joback-Methode auch weitere Methoden ausführlich beschrieben.

Die Verbesserung der Joback-Methode durch Einführung von Wechselwirkungsparametern wird in der Exceldatei ex_03_07_Group_Contribution.xls ( Abb. 1.25) sowohl bei der Berechnung der Siedetemperatur Tb als auch der kritischen Temperatur T cdargestellt.

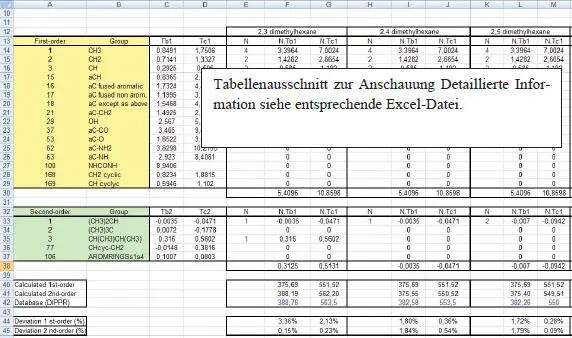
Abb. 1.25. Erweiterte Joback-Berechnung 2. Grades für Isomere

Während man für T bdem 2,3-DMH ein (CH 3) 2CH- mit dem Korrekturwert −0,0035 und ein CH(CH 3)CH(CH 3)-Inkrement mit dem Korrekturewert 0,316 zuordnet, wird dem 2,4-DMH ein (CH 3) 2CH- und dem 2,5-DMH 2 (CH 3) 2CH-Inkremente zugeordnet (vgl. Abb. 1.26).

Abb. 1.26. Inkremente der 2. Ordnung

Der Summenwert ΣG ifür T bbeträgt 5,4096 (F30). Die vollständige, korrigierte Berechnung von ΣGi erfolgt durch

(1.20)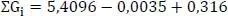

Damit erhält man aus der Joback-Gani-Gleichung

(1.21)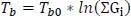

Mit T b0= 222,543 (C8) erhalten wir T b= 375,69 K (F40) nach Joback, d.h. unkorrigiert und 388,19 K (F41) korrigiert. Nach DIPPR beträgt der Siedepunkt 388,76 (F42). Die Abweichung beträgt nur noch 0,15% (F45). Leider fallen die Verbesserungen für die beiden anderen Isomere trotz Verwendung der Korrekturwerte bei Weitem nicht so gut aus (E30:M45). Auch die Berechnung der Siedepunkte für die beiden weiteren Moleküle 2,3,4-Trimethylpentane und n-Propylcyclohexan nach Joback-Gani ergeben sich trotz Verwendung der Korrekturen 2. Ordnung keine nennenswerten Verbesserungen im Vergleich zu den Joback-Ergebnissen (N30:S45).

Die Joback-Gani-Methode unterscheidet sich in Bezug auf den Siedepunkt etwas von der Joback-Methode. Die Gleichung zur Berechnung der Siedetemperatur lautet nach Joback-Gani

(1.22)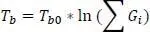

Darin ist T b0= 222,543 K.

Für die kritische Temperatur gilt eine ähnliche Gleichung wie bei Joback.

(1.23)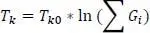

Natürlich sind dann die Inkrementdaten anders.

In der Tabelle „Second-order molecules“ werden die 3 Isomeren von Dimethylhexan betrachtet. In der Zeile 30 und 40 haben alle zunächst dieselben Grunddaten. In den Zeilen 32 bis 37 werden die Strukturen der Isomeren betrachtet und deren Joback-Konstanten verwendet. Diese werden in F41:G41 der zuvor gewonnenen Summe zuaddiert.

(1.24)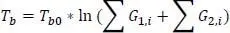

(1.25)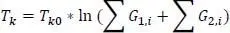

Wie man in den Zeilen 44 und 45 erkennen kann, wird die Genauigkeit durch diese Methode deutlich verbessert. Hier das Beispiel 2,3-diemethylhexan.

Was die Korrekturen bedeuten, geht aus der Grafik in der Excel-Datei hervor, die zwischen T und AE zu finden ist.