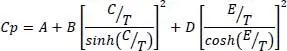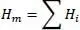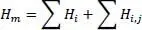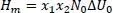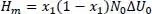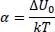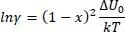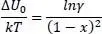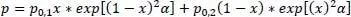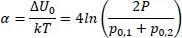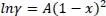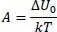Wolfgang Schmidt - Berechnung von Stoffdaten und Phasengleichgewichten mit Excel-VBA

Für gasförmiges Oktan gelten z.B. die folgenden Daten (vgl. Abb. 2.1).

Abb. 2.1. Polynomialkoeffizienten zur Berechnung der isobaren spezifischen Wärmekapazität von Oktan

Daraus lässt sich Abb. 2.2erstellen.

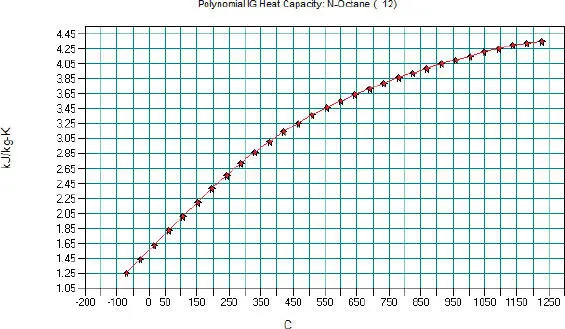
Abb. 2.2. Spezifische Wärmekapizität Cp von N-Oktan, Polynomfunktion nach DIPPR in CHEMCAD

Die neuere Form der DIPPR-Gleichung für gasförmige spezifische Wärmekapazität ist die AliLee-Gleichung.

(2.3)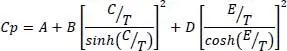

Für Oktan gelten die in Abb. 2.3dargestellten Koeffizienten.

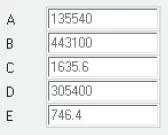
Abb. 2.3. Koeffizienten der Ali-Lee-Gleichung für Oktan

Daraus erhalten wir die folgende grafische Darstellung ( Abb. 2.4).

Beide grafischen Darstellungen ergeben nahezu übereinstimmende Ergebnisse. Die letzte Formel ist in der Lage, das Verhalten von Wasserstoff und Helium bei geringen Temperaturen zu beschreiben.

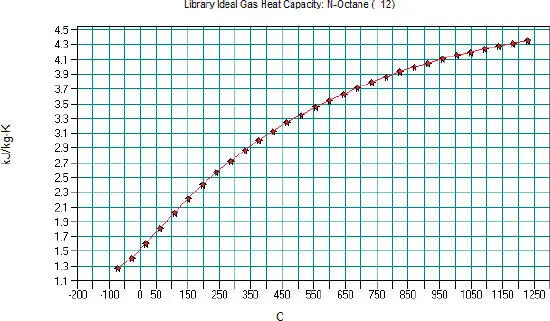
Abb. 2.4. Spezifische Wärmekapizität c pvon N-Oktan, nach der DIPPR-Gleichung 107 in CHEMCAD

Die ideale Mischungsregel für die Enthalpie H mlautet

(2.4)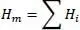

Das heißt, die Enthalpie des Gemisches wird aus den Enthalpien der Reinstoffe durch Addition gebildet. Für die reale Mischungsregel gilt

(2.5)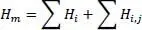

Darin ist H i,jdie binäre Mischungswärme. Mischungswärmen kommen durch Wechselwirkungen der Komponenten zustande. Dabei sind die Wechselwirkungen gemeint, die sich von den Wechselwirkungen der Reinstoffe unterscheiden.

Bei einem Gemisch aus 20 mol-% Ethanol und 80 mol-% Wasser ergibt sich eine Mischungswärme von ca. 900 J/mol. Zum Vergleich diene die Differenz der Verdampfungsenthalpie von Wasser und Ethanol bei 25 °C. Die Verdampfungsenthalpie bei 25 °C beträgt für Ethanol 42510 J/mol und für Wasser 43880 J/mol, berechnet mit CHEMCAD. Die Differenz beträgt 1370 J/mol und liegt damit in der Größenordnung der Mischungswärme.

Es gib eine Beziehung zwischen der Mischungsenthalpie H mund dem zwischenmolekularen Potenzialen ϕ der Moleküle. Das Potenzial zweier Moleküle 1 beträgt ϕ 11, das zweier Moleküle 2 ϕ 22und das der Moleküle 1 und 2 ϕ 12. Somit haben mit N 0= 6,022*10 23mol -1, der Avogadro-Konstante, 1 mol Moleküle das Potenzial

(2.6)

Das Potenzial ϕ berechnet sich nach Lennard-Jones wie in Kapitel 3gezeigt. Für die Mischungswärme gilt näherungsweise

(2.7)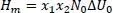

In einem binären Gemisch gilt x 2= 1 – x 1, sodass wir erhalten

(2.8)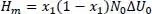

Bei x 1= 0,5 wird H mmaximal. Abweichungen von dieser Symmetrie sind ein Zeichen für ungleiche Moleküle, wie dies z.B. bei Wasser und Ethanol gegeben ist.

Das Potenzial ΔU 0lässt sich auch aus dem Phasengleichgewicht nach der Theorie von van Laar [12] herleiten. Danach gilt für den Partialdruck eines binären Gemisches

(2.9)

Hierin sind p 0der Partialdruck, P der Sattdampfdruck und α gemäß:

(2.10)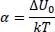

Zur Berechnung von α wird die Boltzmannkonstante k = 1,380648* 10 –23J/mol verwendet.

Andererseits können wir setzen

(2.11)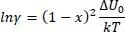

Somit gilt für das Mischungspotenzial in dimensionsloser Form

(2.12)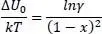

Der Gesamtdruck berechnet sich bei einem binären Gemisch aus beiden Partialdrücken.

(2.13)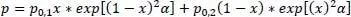

Für x = 0,5 und gleiche Partialdrücke sowie gleiche Potenziale gilt dann für α

(2.14)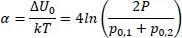

Das Partialdruckdiagramm sieht für verschiedene alpha-Werte wie in Abb. 2.5dargestellt aus.

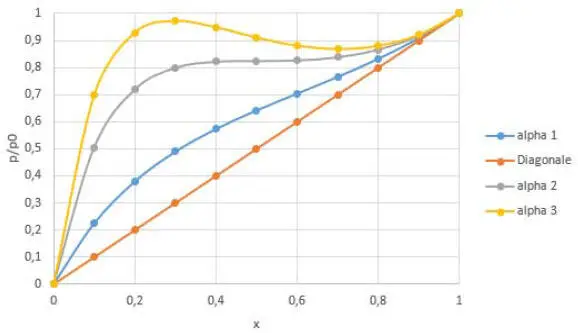
Abb. 2.5. Partialdruckdiagramm nach van Laar mit alpha1 = 1, alpha2 = 2 und alpha3 = 2,4

Die Berechnung befindet sich in der Excel-Datei Mischung.xlsx . Bitte prüfen Sie „Tabelle xy van Laar“. Man erkennt, dass für alpha > 2 drei Lösungen vorliegen, was bedeutet, das zwei Flüssigphasen auftreten. Diese Darstellung ist nicht zu verwechseln mit dem üblichen xy-Diagramm. Vergleicht man damit das Porter-Modell

(2.15)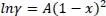

so gilt für die Porter-Konstante

(2.16)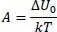

Damit erhalten wir ein xy-Diagramm mit der Porter-Konstante A = 2, entsprechend dem o.g. alpha2 = 2 und einer Flüchtigkeit = 3 wie in Abb. 2.6dargestellt.