Wolfgang Schmidt - Berechnung von Stoffdaten und Phasengleichgewichten mit Excel-VBA

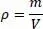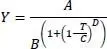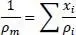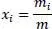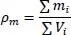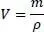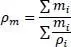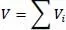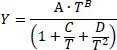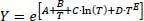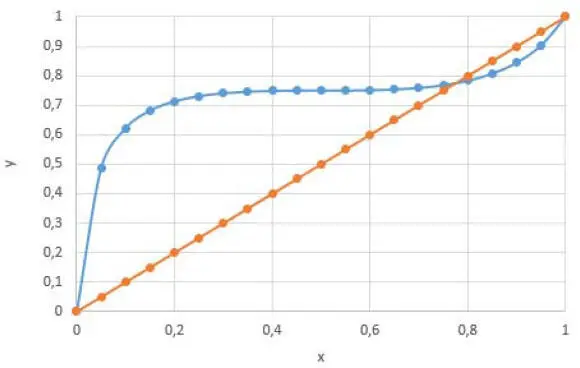
Abb. 2.6. xy-Diagramm nach Porter mit A = 2 und der Flüchtigkeit = 3

Für die o.g. Mischungswärme Ethanol/Wasser wollen wir nun das Mischungspotenzial ΔU 0ermitteln. Dazu verwenden wir die Berechnung des isothermen xy-Diagramms bei 25 °C in CHEMCAD mit NRTL und idealer Gasphase und verwenden die Ergebnisse für x = 0, x = 1 und x = 0,5 wie in der Tabelle Ethanol/Wasser der Excel-Datei Mischung.xlsx vorhanden (vgl. Abb. 2.7).

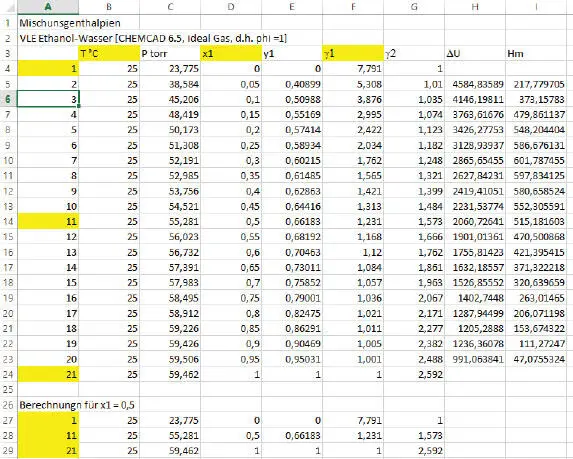
Abb. 2.7. VLE Ethanol/Wasser in Excel

In C4 und C27 befindet sich der Dampfdruck von Wasser bei 25 °C = 23,775 Torr. In C21 und C29 befindet sich der Dampfdruck von Ethanol = 59,462 Torr. In C14 und C28 befindet sich der Gesamtdruck bei x = 0,5 = 55,281. Daraus wird alpha nach der o.g. Formel berechnet und wir erhalten in B31 ( Abb. 2.8) den Wert 1,135.

Abb. 2.8. Berechnung von alpha

Daraus wird γ berechnet mit 1,328 und ΔU 0= 2814 J/mol sowie H m= 703,7 J/mol. Dieser Wert liegt immerhin in der Größenordnung des o.g. Messwertes. Das Diagramm in P5:U17 zeigt die Mischungsenthalpien aus (Dor), die in L4:N30 eingetragen sind (vgl. Abb. 2.9).

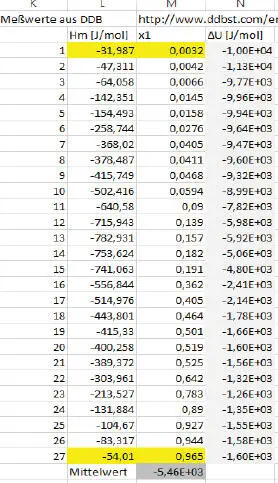
Abb. 2.9. Mischungsenthalpien aus DDBST [7]

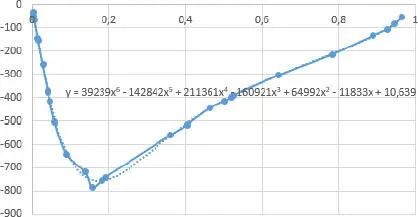
Abb. 2.10. Mischungsenthalie H mvon Ethanol/Wasser nach DDBST [7]

Die Kurve ( Abb. 2.10) wurde in Excel mit einem Polynom 6. Grades angeglichen. Die größte negative Mischungsenthalpie liegt bei ca. 20 mol% Ethanol. Die Excel-Datei Mischungen.xlsx enthält noch weitere Beispiele binärer Gemische.

Ebenfalls sehr wichtig ist die Dichte. Diese ist bekanntlich definiert als

(2.17)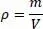

Die Berechnung der gasförmigen Dichte erfolgt nach der Gleichung von SRK (Soave-Redlich-Kwong). Für die Flüssigdichte wird nach DIPPR-Gleichung 105 in CHEMCAD verwendet.

(2.18)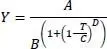

Für N-Oktan gelten die in Abb. 2.11aufgeführten Daten.

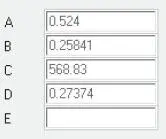
Abb. 2.11. Koeffizienten von N-Oktan für DIPPR-Gleichung 105

Abbildung 2.12 zeigt die grafische Darstellung.

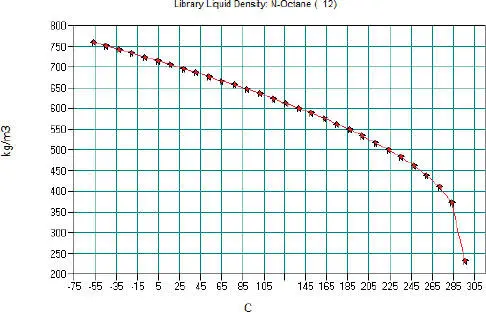
Abb. 2.12.Flüssigdichte von N-Hexan nach der DIPPR-Gleichung 105 in CHEMCAD

Die Berechnung verläuft vom Siedepunkt bis zur kritischen Temperatur. Die ideale Mischungsregel für die gasförmige und flüssige Dichte lautet

(2.19)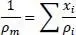

darin ist

(2.20)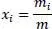

also die Massenkonzentration.

Die Herleitung geht von dieser Gleichung aus:

(2.21)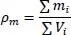

Setzen wir darin

(2.22)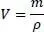

erhalten wir

(2.23)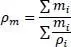

Daraus ergibt sich die o.g. Formel. Bei realen Mischungen gilt jedoch nicht

(2.24)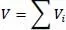

Mithilfe partieller Größen lässt sich die Abweichung von der idealen Mischung zwar grundsätzlich berechnen, jedoch liegen Daten nur für wenige Gemische vor. Für die Berechnung partieller Volumen liegen zwar keinerlei gültigen Grundlagen vor, jedoch ließen sich diese möglicherweise mit komplexen Molekülsimulationen abschätzen. Bei der Betrachtung einer idealen Mischung geht man von der dichtesten Anordnung kugelförmiger Moleküle unterschiedlicher Größe aus. Die dabei entstehenden räumlichen Anordnungen der Moleküle dienen der Berechnung des Potenzials der Mischung.

Die Gasviskosität wird nach Gleichung 2.25(DIPPR-Gleichung 102) berechnet.

(2.25)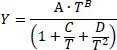

Für gasförmiges N-Oktan gelten die in Abb. 2.13aufgeführten Daten.

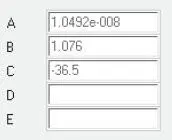
Abb. 2.13. Koeffizienten von N-Oktan für DIPPR-Gleichung 102

Daraus erhält man die grafische Darstellung in Abb. 2.14.

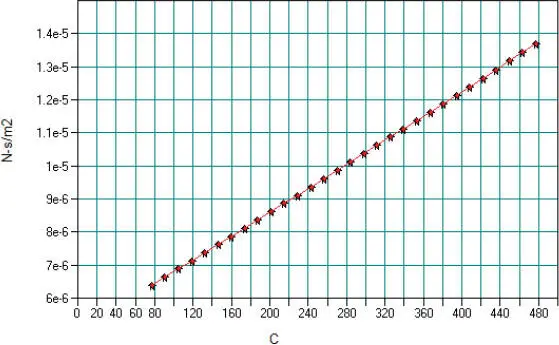
Abb. 2.14. Gasviskosität von N-Oktan nach der DIPPR-Gleichung 102 in CHEMCAD

Die Flüssigviskosität wird mit der Gleichung 2.26(DIPPR-Gleichung 101) berechnet.

(2.26)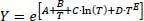

Für flüssiges N-Oktan gelten die in Abb. 2.15aufgeführten Daten.

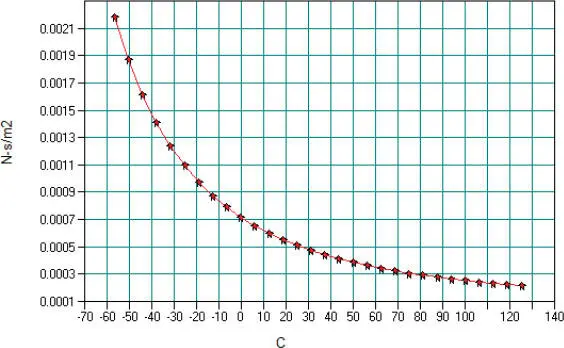
Abb. 2.15. Koeffizienten von N-Oktan für DIPPR-Gleichung 101

Daraus erhält man die grafische Darstellung in Abb. 2.16.