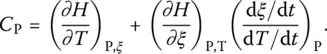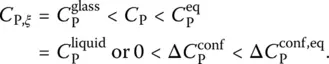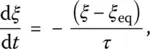Another puzzling fact has been long ago pointed out by Kauzmann [10] who wondered what would happen if the entropy of a supercooled liquid were extrapolated down to temperatures much lower than the experimentally observed T g. The conclusion was that it would become lower than that of the isochemical crystal at a temperature T K, thus termed the Kauzmann temperature ( Table 2), which could suggest that the liquid undergoes a continuous phase transition toward the crystalline phase at T Kanalogous to the critical point of fluids.
One way out of the paradox implies kinetic arguments and assumes that the viscosity of the supercooled liquid diverges at a temperature close to T K. This assumption may be represented by the Vogel–Fulcher–Tammann (VFT) equation ( Chapter 4.1):
(11) 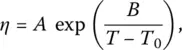
where the temperature T 0of the viscosity divergence is actually close to the Kauzmann temperature ( Table 2) even though they may depend on the specific sample and the method of measurement.
Another way out is to take with great caution the extrapolations of the heat capacity and other thermodynamic functions of the supercooled liquid. As long pointed out [e.g. 11], there is no current theory for these properties in liquid state analogous to the Einstein or Debye models that provide functional forms at all temperatures for heat capacities of crystals.
As derived from strikingly old questions in glass science, these counterintuitive features indicate that glasses cannot be described by equilibrium thermodynamic states only. Nonequilibrium thermodynamics is, therefore, likely to be useful to characterize glasses and the glass transition.
5 Nonequilibrium Thermodynamics of the Glass Transition
The questions raised by the Kauzmann paradox or the PD ratio clearly illustrate the need for a more fundamental thermodynamic description of the glass transition. Following the pioneering work of Tool [12, 13] and Davies and Jones [9], different approaches and phenomenological models have been developed to deal with the glass transition range itself, many within the framework of classical nonequilibrium thermodynamics [4, 11].
The starting point has been the phenomenological concept of fictive temperature ( T f) propounded by Tool [12, 13] to characterize the state of a relaxing system at any time. This temperature is similar to an order parameter ξ . It thus overcomes the limitations of the fixed limiting temperature T M, which characterizes only the point at which internal equilibrium is suddenly lost in a quenched state. On an analogous basis, a more detailed description is made in terms of two‐temperature thermodynamics [14] whereby the vibrational and configurational degrees of freedom are distinguished by a “classical” temperature for fast modes (phonons bath), and an effective temperature for the slow modes, respectively.
The first physical models have then relied on two different approaches. In free‐volume theories, one generally considers that the dynamics of the system is determined by the free space present around its atoms, which makes configurational rearrangements more or less easy. In entropy theories, among which that of Adam‐Gibbs is the best known [15], the same determining role is attributed to configurational entropy. In other words, these theories assign the strong increase of relaxation times with decreasing temperatures and the eventual structural freezing in to decreases of either free volume or configurational entropy. Other more recent theories of the glass transition rely on mode coupling, random first‐order transitions or energy‐landscape descriptions [e.g. 16]. These different approaches have the common goal of finding the exact expression for the structural relaxation time, or its distribution, as a function of controlling parameters such as temperature or pressure, or structural order parameter.
For the sake of simplicity, let us consider here conditions of constant pressure. If the additional parameter ξ is taken into account, the total differential of the enthalpy of a system can be written as the sum of two contributions (considering pressure, the generalization to three contributions would be obvious):
(12) 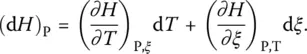
The isobaric heat capacity is written as:
( 13) 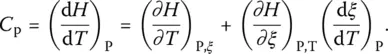
The first term on the right‐hand side is the heat capacity at constant ξ , i.e. 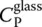 , and the second, the configurational contribution
, and the second, the configurational contribution 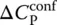 as defined by Eq. (6). To account for the kinetic nature of the glass transition, it is then necessary to rewrite Eq. (13)as:
as defined by Eq. (6). To account for the kinetic nature of the glass transition, it is then necessary to rewrite Eq. (13)as:
( 14) 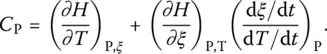
When the rate of change of ξ becomes much smaller than the rate of change of temperature, (d ξ /d t ) P≪ (d T /d t ) P, the configurational contribution is negligible.
Hence, it is the ratio between these two rates that is controlling the relative value of the experimentally recorded configurational heat capacity. This ratio is maximum in the supercooled liquid state, and decreases throughout the glass transition range to become negligible in the glassy state (cf. Figure 3). There, only the first right‐hand side term in Eq. (14)contributes:
(15) 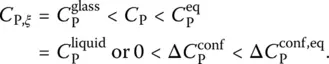
The next step thus consists in taking into account the time dependence of ξ at every temperature through the temperature dependence of the relaxation time τ . The simplest way to do this is to assume a simple exponential decay for ξ at fixed temperature and pressure:
( 16) 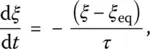
where ξ eq( P , T ) is the equilibrium value of the order parameter, i.e. a variable characterizing the liquid structure that depends only on P and T . Although the relaxation time itself has been given different temperature dependences with Arrhenius, VFT, or others laws ( Chapter 3.7), the important point is that they are all of an exponential nature with respect to T or P to ensure the structural freezing‐in of the system.
Interesting applications of these concepts have been made with the lattice‐hole model of liquids, which has the advantage of lending itself to an evaluation of the order parameter ξ . Schematically, this model considers a liquid as a lattice in which disorder is represented by unoccupied sites whose fraction x depends on both temperature and pressure [17]. From the equilibrium value of the order parameter, it is thus possible to solve the linear differential Eq. (16)to find its temperature dependence and, then, to calculate the variations of the heat capacity within the glass transition range under varied conditions [18]. Likewise, the configurational Gibbs free energy may also be computed analytically as a function of temperature, pressure, and order parameter. A similar approach has been followed to incorporate the effects of pressure in the expression of the structural relaxation time for determining also how the heat capacity, thermal expansion coefficient, and isothermal compressibility vary under different conditions [19].
Читать дальше

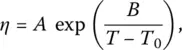
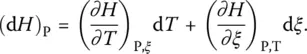
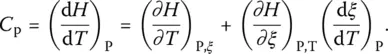
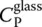 , and the second, the configurational contribution
, and the second, the configurational contribution 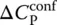 as defined by Eq. (6). To account for the kinetic nature of the glass transition, it is then necessary to rewrite Eq. (13)as:
as defined by Eq. (6). To account for the kinetic nature of the glass transition, it is then necessary to rewrite Eq. (13)as: