( 3) 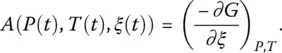
The affinity A , expressed in J/mol, is the intensive conjugate variable of ξ . All time dependences are thus embedded into the time variations of the internal parameter ξ , or A , and of the other variables that are controlled experimentally (e.g. T , P ).
For a relaxing system, the instantaneous entropy production was simply written by De Donder as the product of the thermodynamic force and the corresponding flux [4],
Table 1 Thermodynamic states in terms of affinity and its derivatives and in terms of rate of advancement of the process.
| Rate of advancement d ξ/ d t (extensive, mol/s) |
d ξ/ d t = 0 |
d ξ/ d t ≠ 0 |
| Affinity A (intensive, J/mol) |
| A = 0 and d A = 0 |
True equilibrium; liquid state; σ i = 0 |
Unphysical |
| A = 0 and d A ≠ 0 |
Isomassic state; σ i = 0 |
False equilibrium; nonequilibrium state; σ i = 0 |
| A ≠ 0 and d A = 0 |
Isomassic, isoaffine state; σ i = 0 |
Isoaffine state; σ i ≠ 0 |
| A ≠ 0 and d A ≠ 0 |
Nonequilibrium; glassy state; σ i = 0 |
Nonequilibrium; viscous state; σ i ≠ 0 |
Liquid, glass, and relaxing liquid states are indicated by gray cells. The other cells indicate particular states that can be encountered or not during the glass transition. The value of the rate of production of entropy is indicated in each cell.
(4) 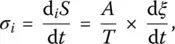
where the thermodynamic force actually is A/T , for the sake of dimensional analysis (the entropy production being in W/K).
Regarding the glass transition, the problem boils down to know A and ξ (or d ξ /d t ) and how they evolve with time. Depending on the values of both parameters, however, at this point several cases must be distinguished because not all of them are relevant ( Table 1). The first and simplest case is that for which both A and d ξ /d t are zero. It is that of the equilibrium liquid, which will thus be first considered in its metastable, supercooled extension.
Although the liquid state is generally far from simple, it can be considered as an equilibrium reference at viscosities ( η ) low enough that flow is easy, i.e. at high‐enough temperatures at the pressure considered. In that case, the diffusion of microscopic entities, be they molecules or atoms, obeys the Stokes‐Einstein relation, which relates the diffusivity D to the temperature and viscosity with:
(5) 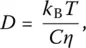
where the coefficient C is a geometrical factor fixed by the boundary condition of the flow.
From its position at time t 0, a diffusing entity travels a kind of random walk over an average distance 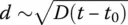 as a function of time. For low‐viscosity liquids and high temperatures, D is high so that entities explore a great many different positions and configurations in a time shorter than that needed to perform a physical measurement. They do it through degrees of freedom that include not only thermal motions of translation, rotation, and vibration but also the complex kinds of atomic motions collectively termed configurational , which are governed by strong short‐range repulsions and long‐range attractions in molecular liquids. The measurement then averages out all these configurations.
as a function of time. For low‐viscosity liquids and high temperatures, D is high so that entities explore a great many different positions and configurations in a time shorter than that needed to perform a physical measurement. They do it through degrees of freedom that include not only thermal motions of translation, rotation, and vibration but also the complex kinds of atomic motions collectively termed configurational , which are governed by strong short‐range repulsions and long‐range attractions in molecular liquids. The measurement then averages out all these configurations.
Picturing these motions at a microscopic scale is difficult, however, especially for complex liquids or melts with various interacting entities. In various types of glass‐forming liquids [5], local order can nonetheless be described in terms of degree of polymerization, formation of channels or sub‐lattices, or formation of interpenetrating networks. Like the advancement of a chemical reaction, such structural features may be described in terms of the aforementioned parameter ξ . In internal thermodynamic equilibrium, i.e. in the liquid state, ξ is equal to ξ eq( T,P ), but not in the glass transition range where ξ ( t ) becomes a function of T ( t ), P ( t ), and A ( t ), revealing its nonequilibrium nature. Below the glass transition range, where the relaxation time of the configurational degrees of freedom exceeds the experimental timescale, they cease to contribute to the measured property. At temperature low enough, the structure then eventually freezes in for good in one state defined by one particular value of ξ ( t ), which becomes independent of the external parameters T and P .
From a practical standpoint, the timescale defined by the viscosity of the material is important to determine the temperature at which the system will fall out of equilibrium when observed at the timescale of a particular experiment. There is not yet a unique model for describing relaxation phenomena in all glass‐forming liquids ( Chapter 3.7), whether strong or fragile with Arrhenian or non‐Arrhenian viscosities, respectively [6]. In measurements of macroscopic properties, one nonetheless considers generally that experimental timescales τ expare of the order of τ exp~10 2– 10 3seconds. The viscosity should then be of the order of 10 12Pa.s or 10 13P for structural relaxation to be complete under these conditions. To stress the usually tremendous variations of viscosity down to the glass transition, it will suffice to note that the viscosities of stable liquids (i.e. above the melting or liquidus temperature) range from 10 −3to 10 2Pa.s depending on chemical composition and structural type.
4 Glass as a Nonequilibrium Substance
Time‐dependent effects appearing at the glass transition are clearly observed in the heat capacities measured for PVAc ( Figure 2), which is a model polymeric system extensively studied because of its excellent glass‐forming ability and standard T gclose to room temperature. The observed hysteresis loop between cooling and heating demonstrates that the heat capacity does not only depend on T and P but also on time. Moreover, upon heating, the heat capacity shows a typical overshoot, i.e. an endothermic event, named structural recovery process. To come back to the initial liquid state, the system needs to recover the amount of internal enthalpy that has previously been lost. From such measurements, it is possible to determine the configurational contribution to the heat capacity  . Here, it is defined by the difference at every temperature between the heat capacities actually measured and estimated for the glass phase:
. Here, it is defined by the difference at every temperature between the heat capacities actually measured and estimated for the glass phase:
Читать дальше

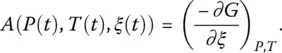
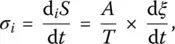
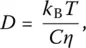
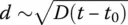 as a function of time. For low‐viscosity liquids and high temperatures, D is high so that entities explore a great many different positions and configurations in a time shorter than that needed to perform a physical measurement. They do it through degrees of freedom that include not only thermal motions of translation, rotation, and vibration but also the complex kinds of atomic motions collectively termed configurational , which are governed by strong short‐range repulsions and long‐range attractions in molecular liquids. The measurement then averages out all these configurations.
as a function of time. For low‐viscosity liquids and high temperatures, D is high so that entities explore a great many different positions and configurations in a time shorter than that needed to perform a physical measurement. They do it through degrees of freedom that include not only thermal motions of translation, rotation, and vibration but also the complex kinds of atomic motions collectively termed configurational , which are governed by strong short‐range repulsions and long‐range attractions in molecular liquids. The measurement then averages out all these configurations. . Here, it is defined by the difference at every temperature between the heat capacities actually measured and estimated for the glass phase:
. Here, it is defined by the difference at every temperature between the heat capacities actually measured and estimated for the glass phase:










