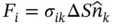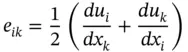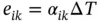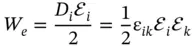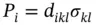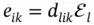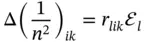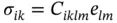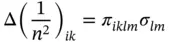where ris the radius-vector connecting the element Δland the observation point (see Figure 1.12). In turn, magnetic dipole moment, μ d, is defined as an integral over the volume containing the current density distribution J:
(1.8) 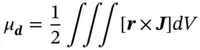
Axial vectors are considered when analyzing magnetic symmetry and magnetic symmetry groups ( Chapter 11).
Tensor of rank 2 has two independent indices i , k = 1, 2, 3. As a rule, it linearly connects two vectors, e.g. the vectors of the electric displacement field, D i, and external electric field, ℰ k, i.e.  , as tensor of dielectric permittivity, ε ik, does (see Chapter 8). Another example is the density of electric current, J i, and electric field, ℰ k, connected by the electrical conductivity tensor ρ ik, i.e.
, as tensor of dielectric permittivity, ε ik, does (see Chapter 8). Another example is the density of electric current, J i, and electric field, ℰ k, connected by the electrical conductivity tensor ρ ik, i.e.  (see Chapter 4). In further analyses, we will omit the summation symbols and use the reduced record (according to the Einsteinconvention) for tensor relationships, e.g.
(see Chapter 4). In further analyses, we will omit the summation symbols and use the reduced record (according to the Einsteinconvention) for tensor relationships, e.g.
(1.9) 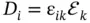
(1.10) 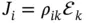
There are two important field tensors of second rank, which are in common use. These are the stress and strain tensors. Stress tensor, σ ik, connects vector of external force, F i, applied to a certain crystal area, Δ S , and unit vector, 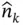 , normal to this area:
, normal to this area:
(1.11) 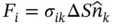
Based on the mechanical equilibrium of the stressed solid, it is possible to prove that stress tensor ( Eq. (1.11)) is symmetric one, i.e. σ ik= σ ki. Regarding strain tensor, it connects the deformation vector, u i, in the vicinity of a given point and the radius-vector of this point, x i. Deformation vector determines the difference in the distances between closely located points near x iin the deformed and non-deformed states of the crystal. To provide local information on the deformed state, strain tensor, e ik, is defined in the differential form:
(1.12) 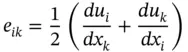
Evidently, the strain tensor, defined by Eq. (1.12), is symmetric one, i.e. e ik= e ki.
Furthermore, inter-atomic distances within a crystal are also changed upon heating (see Chapter 3). In that sense, a crystal heated up to some temperature, T 1, is in different “deformation” state as compared with its initial state at temperature, T 0. Thus produced relative change in lattice parameters is mathematically equivalent to strain ( Eq. (1.12)). Tensor of second rank, which relates e ikto the temperature increase, Δ T = T 1− T 0(tensor of rank zero, i.e. scalar), is called as tensor of linear expansion coefficients, α ik:
(1.13) 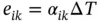
Note that both crystal states, at T = T 0and T = T 1,are thermodynamically equilibrium states at respective temperatures, and, therefore, no elastic energy is stored in such “deformed crystal,” whenever the temperature change is homogeneous across the crystal. The only energy difference between these two states is in free energy, which is temperature dependent.
Tensor of second rank may also connect a scalar and two vectors, as tensor of dielectric permittivity, ℰ ik, does for energy density, W e, of electromagnetic field within a crystal:
(1.14) 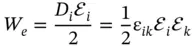
By using tensor representation for the electric displacement field (see Eq. (1.9)), we find that the energy density is quadratic with respect to the applied electric field, ℰ i.
Tensor of third rank has three indices i, k, l = 1, 2, 3. It connects tensor of second rank and vector, e.g. stress, σ ik, and induced electric polarization, P i:
(1.15) 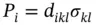
as for direct piezoelectric effect, or strain, e ik, and applied electric field, ℰ i:
(1.16) 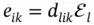
for converse piezoelectric effect, both discussed in detail in Chapter 12. Another example is tensor, r lik, of the linear electro-optic effect (the Pockelseffect, also mentioned in Chapter 12). This tensor of third rank connects the change, Δ n ik, of refractive index, n , (which can be described in terms of the second rank tensor) under applied electric field, with the electric field vector, ℰ l:
(1.17) 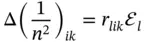
For the fourth rank tensor, there are several optional ways for its construction. It may connect two tensors of rank 2, e.g. stress, σ ik, and strain, e lm, as the stiffness tensor, C iklm(tensor of elastic modules used in Chapter 3), does:
(1.18) 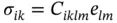
Similar tensor object, π iklm, is used to describe the photo-elastic effect in crystals, which provides the change of refractive index under applied stress:
(1.19) 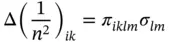
Another possibility is to connect tensor of second rank (e.g. strain tensor, e ik) and two vectors (e.g. quadratic form of electric field, ℰ lℰ m) as for electrostriction effect, g iklm:
Читать дальше

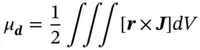
 , as tensor of dielectric permittivity, ε ik, does (see Chapter 8). Another example is the density of electric current, J i, and electric field, ℰ k, connected by the electrical conductivity tensor ρ ik, i.e.
, as tensor of dielectric permittivity, ε ik, does (see Chapter 8). Another example is the density of electric current, J i, and electric field, ℰ k, connected by the electrical conductivity tensor ρ ik, i.e.  (see Chapter 4). In further analyses, we will omit the summation symbols and use the reduced record (according to the Einsteinconvention) for tensor relationships, e.g.
(see Chapter 4). In further analyses, we will omit the summation symbols and use the reduced record (according to the Einsteinconvention) for tensor relationships, e.g.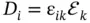
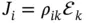
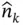 , normal to this area:
, normal to this area: