In the absence of the long-range translational symmetry, however, as in quasicrystals, one can find additional rotation axes, e.g. fivefold ( 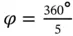 = 72°), as for 2D construction shown in Figure 1.3or for icosahedral symmetry in 3D. The latter can be found in two Platonicbodies: regular icosahedrons and dodecahedrons. Regular dodecahedron has 12 pentagonal faces and 20 vertices, in each of them three faces meet ( Figure 1.5). Therefore, the fivefold axes are normal to the pentagonal faces. In contrast, regular icosahedron has 20 triangular faces and 12 vertices, in each of them five faces meet ( Figure 1.6). Therefore, the fivefold axes connect the body center and each vertex. Note that regular pentagon (plane figure) has central angle 72° and is characterized by the so-called golden ratio τ (the ratio between the pentagon diagonal, d p, and pentagon edge, a p, see Figure 1.7):
= 72°), as for 2D construction shown in Figure 1.3or for icosahedral symmetry in 3D. The latter can be found in two Platonicbodies: regular icosahedrons and dodecahedrons. Regular dodecahedron has 12 pentagonal faces and 20 vertices, in each of them three faces meet ( Figure 1.5). Therefore, the fivefold axes are normal to the pentagonal faces. In contrast, regular icosahedron has 20 triangular faces and 12 vertices, in each of them five faces meet ( Figure 1.6). Therefore, the fivefold axes connect the body center and each vertex. Note that regular pentagon (plane figure) has central angle 72° and is characterized by the so-called golden ratio τ (the ratio between the pentagon diagonal, d p, and pentagon edge, a p, see Figure 1.7):
(1.6) 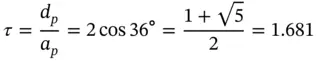
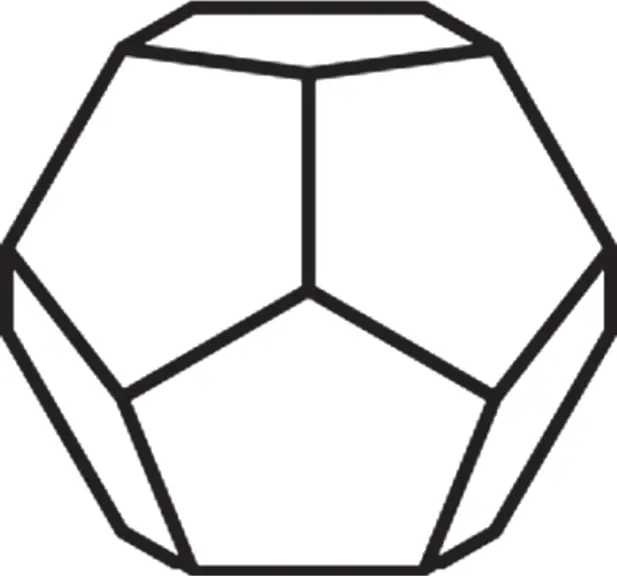
Figure 1.5Dodecahedron sculpted by 12 pentagonal faces.

Figure 1.6Icosahedron sculpted by 20 triangular faces.
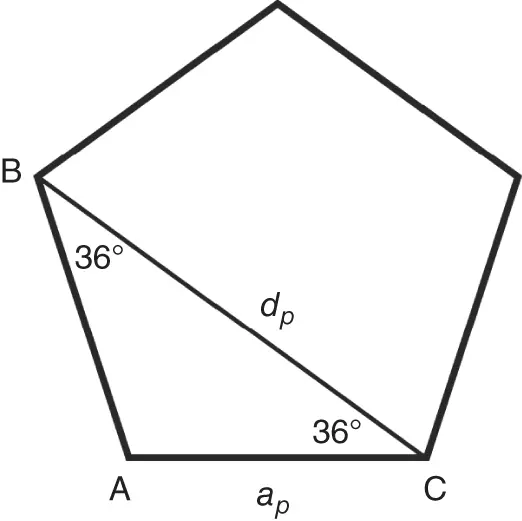
Figure 1.7Regular pentagon with edges equal a pand diagonals equal d p. The ratio, 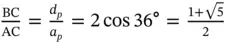 , is called the golden ratio ( Eq. (1.6)).
, is called the golden ratio ( Eq. (1.6)).
which is of great importance to the quasicrystal diffraction conditions (described later in this chapter).
Permitted combinations of local symmetry elements (totally 32 in regular crystals) are called point groups. A set of different crystals, possessing the same point group symmetry, form certain crystal class. Point group symmetry is responsible for anisotropy of physical properties in crystals, as explained in more detail further in this chapter.
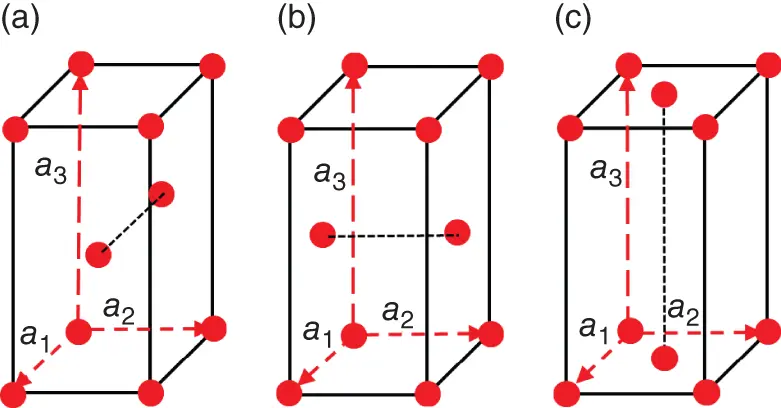
Figure 1.8Unit cells of the following side-centered Bravaislattices: A-type (a), B-type (b), C-type (c). Translation vectors, a 1, a 2, a 3, are indicated by dashed arrows.
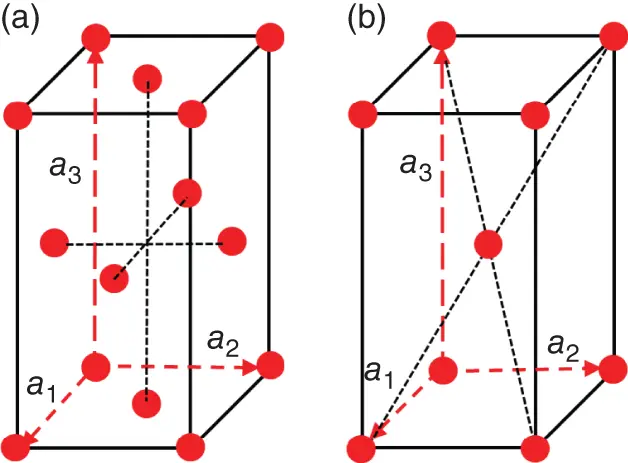
Figure 1.9Unit cells of the following centered Bravaislattices: (a) face-centered (F-type) and (b) body-centered (I-type). Translation vectors, a 1, a 2, a 3, are indicated by dashed arrows.
Bravaislattices defined by Eq. (1.1)are primitive (P) since they effectively contain only one atom per unit cell. However, in some symmetry systems, the same local symmetry will be held for centered Bravaislattices, in which the symmetry-related equivalent points are not only the corners (vertices) of the unit cell (as for primitive lattice), but also the centers of the unit cell faces or the geometrical center of the unit cell itself ( Figures 1.8and 1.9). Such lattices are conventionally called side-centered (A, B, or C), face-centered (F), and body-centered (I). In side-centered modifications of the type A, B, or C, additional equivalent points are in the centers of two opposite faces, being perpendicular, respectively, to the a 1-, a 2-, or a 3- translation vectors ( Figure 1.8). In the face-centered modification, F, all faces of the Bravaisparallelepiped (unit cell) are centered ( Figure 1.9). For the cubic symmetry system, the F-centered Bravaislattice is called face-centered cubic (fcc). In the body-centered modification, I, the center of the unit cell is symmetry-equivalent to the unit cell vertices ( Figure 1.9). For the cubic symmetry system, the I-modification of the Bravaislattice is called body-centered cubic (bcc). Accounting of centered Bravaislattices increases their total amount up to 14.
In some cases, the choice of Bravaislattice is not unique. For example, fcc lattice can be represented as rhombohedral one with a R= a / 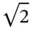 and α = 60° ( Figure 1.10a). Rhombohedral lattice is a primitive one and comprises one atom per unit cell instead four atoms in the fcc unit cell. Similarly, bcc lattice can be represented in the rhombohedral setting with a R= a
and α = 60° ( Figure 1.10a). Rhombohedral lattice is a primitive one and comprises one atom per unit cell instead four atoms in the fcc unit cell. Similarly, bcc lattice can be represented in the rhombohedral setting with a R= a 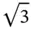 /2 and α = 109.47° ( Figure 1.10b). In this case, the rhombohedral lattice comprises one atom per unit cell instead two atoms in the bcc unit cell. We will widely use these settings in Chapter 2considering the shapes of Brillouinzones. Minimizing number of atoms in the unit cell substantially reduces the calculation complexity of different physical properties in crystals.
/2 and α = 109.47° ( Figure 1.10b). In this case, the rhombohedral lattice comprises one atom per unit cell instead two atoms in the bcc unit cell. We will widely use these settings in Chapter 2considering the shapes of Brillouinzones. Minimizing number of atoms in the unit cell substantially reduces the calculation complexity of different physical properties in crystals.
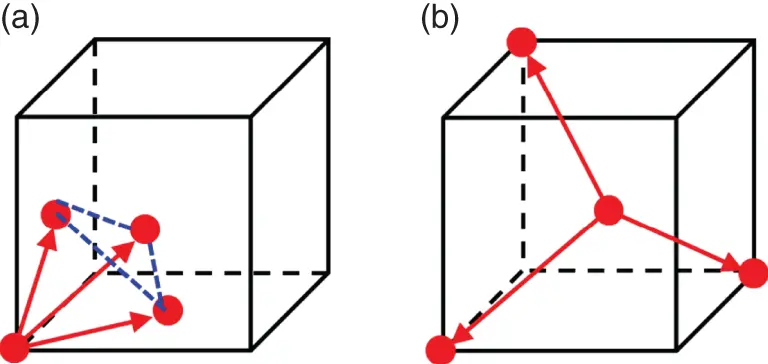
Figure 1.10Lattice translations (red arrows) in the rhombohedral setting of the fcc (a) and bcc (b) lattices.
Table 1.1Summary of possible symmetries in regular crystals.
| Crystal symmetry |
Bravais lattice type |
Crystal classes (point groups) |
| Triclinic |
P |
1 , 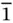 |
| Monoclinic |
P; B, or C |
m , 2, 2/ m |
| Orthorhombic |
P; A, B, or C; I; F |
mm 2, 222, mmm |
| Tetragonal |
P; I |
4, 422, 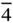 , , 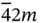 , 4/ m , 4 mm , 4/ mmm , 4/ m , 4 mm , 4/ mmm |
| Cubic |
P; I (bcc); F (fcc) |
23, 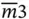 , 432, , 432, 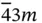 , , 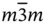 |
| Rhombohedral (trigonal) |
P ( R ) |
3, 32, 3 m , 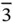 , , 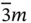 |
| Hexagonal |
P |
6, 622, 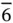 , , 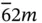 , 6/ m , 6 mm , 6/ mmm , 6/ m , 6 mm , 6/ mmm |
Symmetry systems, types of Bravaislattices, and distribution of crystal classes (point groups) among them are summarized in Table 1.1.
Читать дальше

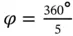 = 72°), as for 2D construction shown in Figure 1.3or for icosahedral symmetry in 3D. The latter can be found in two Platonicbodies: regular icosahedrons and dodecahedrons. Regular dodecahedron has 12 pentagonal faces and 20 vertices, in each of them three faces meet ( Figure 1.5). Therefore, the fivefold axes are normal to the pentagonal faces. In contrast, regular icosahedron has 20 triangular faces and 12 vertices, in each of them five faces meet ( Figure 1.6). Therefore, the fivefold axes connect the body center and each vertex. Note that regular pentagon (plane figure) has central angle 72° and is characterized by the so-called golden ratio τ (the ratio between the pentagon diagonal, d p, and pentagon edge, a p, see Figure 1.7):
= 72°), as for 2D construction shown in Figure 1.3or for icosahedral symmetry in 3D. The latter can be found in two Platonicbodies: regular icosahedrons and dodecahedrons. Regular dodecahedron has 12 pentagonal faces and 20 vertices, in each of them three faces meet ( Figure 1.5). Therefore, the fivefold axes are normal to the pentagonal faces. In contrast, regular icosahedron has 20 triangular faces and 12 vertices, in each of them five faces meet ( Figure 1.6). Therefore, the fivefold axes connect the body center and each vertex. Note that regular pentagon (plane figure) has central angle 72° and is characterized by the so-called golden ratio τ (the ratio between the pentagon diagonal, d p, and pentagon edge, a p, see Figure 1.7):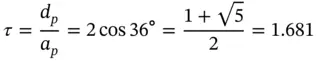



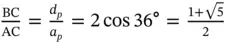 , is called the golden ratio ( Eq. (1.6)).
, is called the golden ratio ( Eq. (1.6)).

 and α = 60° ( Figure 1.10a). Rhombohedral lattice is a primitive one and comprises one atom per unit cell instead four atoms in the fcc unit cell. Similarly, bcc lattice can be represented in the rhombohedral setting with a R= a
and α = 60° ( Figure 1.10a). Rhombohedral lattice is a primitive one and comprises one atom per unit cell instead four atoms in the fcc unit cell. Similarly, bcc lattice can be represented in the rhombohedral setting with a R= a 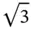 /2 and α = 109.47° ( Figure 1.10b). In this case, the rhombohedral lattice comprises one atom per unit cell instead two atoms in the bcc unit cell. We will widely use these settings in Chapter 2considering the shapes of Brillouinzones. Minimizing number of atoms in the unit cell substantially reduces the calculation complexity of different physical properties in crystals.
/2 and α = 109.47° ( Figure 1.10b). In this case, the rhombohedral lattice comprises one atom per unit cell instead two atoms in the bcc unit cell. We will widely use these settings in Chapter 2considering the shapes of Brillouinzones. Minimizing number of atoms in the unit cell substantially reduces the calculation complexity of different physical properties in crystals.
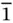
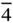 ,
, 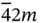 , 4/ m , 4 mm , 4/ mmm
, 4/ m , 4 mm , 4/ mmm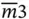 , 432,
, 432, 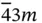 ,
, 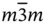
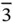 ,
, 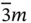
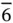 ,
, 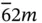 , 6/ m , 6 mm , 6/ mmm
, 6/ m , 6 mm , 6/ mmm










