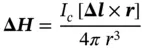The number of high-order symmetry elements, i.e. the threefold, fourfold, and sixfold rotation axes, which can simultaneously appear in a crystal, is also symmetry limited. For threefold rotation axis, this number may be one, in trigonal classes, or four, in cubic classes; for fourfold rotation axes – one in tetragonal classes or three in some cubic classes, while for sixfold rotation axis – only one in all hexagonal classes (see Appendix 1.A).
The presence or absence of an inversion center in a crystal is of upmost importance to many physical properties. For example, ferroelectricity and piezoelectricity (see Chapter 12) do not exist in centro-symmetric crystals, i.e. in those having inversion center. In this context, it is worth to note that any Bravaislattice is centro-symmetric. For primitive lattices, this conclusion follows straightforwardly from Eq. (1.1). Centered (non-primitive) Bravaislattices certainly do not refute this statement ( Figures 1.8and 1.9). However, only 11 crystal classes of total 32, in fact, are centro-symmetric. Even for high cubic symmetry, only two classes are centro-symmetric, i.e. 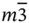 and
and 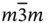 ( Table 1.1). Evidently, the loss of an inversion center can happen in crystals, which are built of several Bravaislattices, their origins being shifted relative to each other. We stress that it is necessary, but not sufficient condition for the loss of inversion center. For illustration, let us consider Si (diamond structure) and GaAs (zinc blende or sphalerite structure) crystals. Both comprise two fcc lattices shifted relative to each other by one quarter of a space cube diagonal. The difference is that in silicon these sub-lattices are occupied by identical atoms (Si), whereas in GaAs – separately by Ga and As. In a result, Si is centro-symmetric (class
( Table 1.1). Evidently, the loss of an inversion center can happen in crystals, which are built of several Bravaislattices, their origins being shifted relative to each other. We stress that it is necessary, but not sufficient condition for the loss of inversion center. For illustration, let us consider Si (diamond structure) and GaAs (zinc blende or sphalerite structure) crystals. Both comprise two fcc lattices shifted relative to each other by one quarter of a space cube diagonal. The difference is that in silicon these sub-lattices are occupied by identical atoms (Si), whereas in GaAs – separately by Ga and As. In a result, Si is centro-symmetric (class 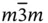 ) that can be easily proved by setting inversion center at point (⅛,⅛,⅛), i.e. in the middle between the origins of two centro-symmetric fcc Si sub-lattices ( Figure 1.11a). This recipe can hardly be used in case of GaAs since there is no symmetry operation that converts Ga to As ( Figure 1.11b). Therefore, GaAs is non-centro-symmetric crystal belonging to class
) that can be easily proved by setting inversion center at point (⅛,⅛,⅛), i.e. in the middle between the origins of two centro-symmetric fcc Si sub-lattices ( Figure 1.11a). This recipe can hardly be used in case of GaAs since there is no symmetry operation that converts Ga to As ( Figure 1.11b). Therefore, GaAs is non-centro-symmetric crystal belonging to class 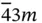 and revealing significant piezoelectric effect.
and revealing significant piezoelectric effect.
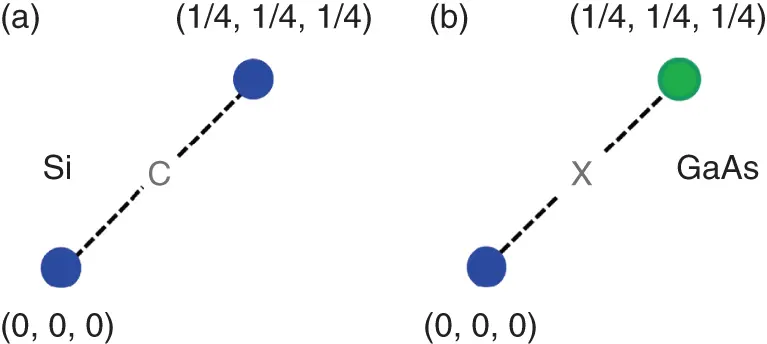
Figure 1.11The presence of inversion center ( C) in diamond structure (a) and its loss ( X) in zinc-blende structure (b). Dissimilar atoms are indicated by different colors.
Combining local symmetry elements with translations creates novel elements of spatial symmetry – glide planes and screw axes. Therefore, spatial symmetry is a combination of local (point) symmetry and translational symmetry. As a result, 32 point groups + 14 Bravaislattices produce 230 space groups describing all possible variants of crystal symmetry, associated with charge distributions, i.e. related to geometrical points and polar vectors. Magnetic symmetry, linked to magnetic moments (axial vectors, see Section 1.2), will be discussed in Chapter 11.
1.2 Symmetry and Physical Properties in Crystals
Crystal symmetry imposes tight restrictions on its physical properties. Term “properties” relates to those that can be probed by regular (macroscopic) optical, mechanical, electrical, and other measurements, averaging over the actual atomic-scale periodicity of physical characteristics. Note that complete spatial symmetry of the crystal is revealed in diffraction measurements using quantum beams (X-rays, neutrons, electrons) with wavelengths comparable with translational periodicity. Note that crystal characteristics, even averaged over many translation periods, show anisotropy which is dictated by the crystal point group. Within this averaged approach, the symmetry constraints are formulated by means of the so-called Neumann'sprinciple: the point group of the crystal is a sub-group of the group describing any of its physical properties. In simple words, the symmetry of physical property of the crystal cannot be lower than the symmetry of the crystal: it may be only equivalent or higher.
In practical terms, it means that if physical property is measured along certain direction within the crystal and then the atomic network is transformed according any symmetry element of its point group and measurement repeats, we expect to obtain the measurable effect of the same magnitude and sign as before. Any deviation will contradict particular crystalline symmetry and, thus, the Neumann'sprinciple. Using mathematical language, physical properties are, generally, described by tensors of different rank, for which the transformation rules under local symmetry operations are well-known. Tensor rank defines the number of independent tensor indices, i, k, l , m, …, each of them being run between 1 and 3, if the 3D space is considered. In most cases, physical property is the response to external field applied to the crystal. Note that external fields are also described by tensors, which are called field tensors to distinguish them from crystal (material) tensors.
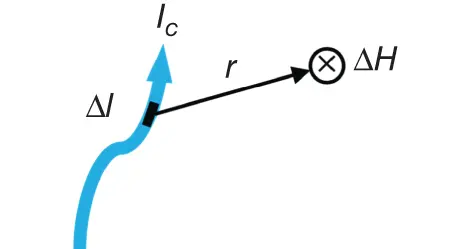
Figure 1.12Illustration of the Biot–Savartlaw ( Eq. (1.7)).
Tensors of zero rank are scalars. It means that they do not change at all under coordinate transformations related to symmetry operations. As an example of scalar characteristics, we can mention the mass density of a crystal. Tensor of rank one is a vector. It has one index i = 1,2,3, which enumerates vector projections on three mutually perpendicular coordinate axes within Cartesian( Descartes) coordinate system. It is easy to point out field vectors, for example, an applied electric field, ℰ i, or electric displacement field, D i. As crystal vector, existing with no external fields, one can recall the vector of spontaneous polarization, 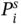 , in ferroelectric crystals (see Chapter 12). Spontaneous polarization, as well as polarization, P i, induced by external electric field, is defined as the sum of elementary dipole moments per unit volume. Note that polarization Pis polar vector having three projections, P i, as e.g. radius-vector r(with projections, x i). There exist also axial vectors (or pseudo-vectors), i.e. vector products (cross products) of polar vectors, which are used to describe magnetic fields and magnetic moments. In fact, magnetic field, ΔH, produced by the element Δlof a conducting wire carrying electric current, I c, is described by the Biot–Savartlaw:
, in ferroelectric crystals (see Chapter 12). Spontaneous polarization, as well as polarization, P i, induced by external electric field, is defined as the sum of elementary dipole moments per unit volume. Note that polarization Pis polar vector having three projections, P i, as e.g. radius-vector r(with projections, x i). There exist also axial vectors (or pseudo-vectors), i.e. vector products (cross products) of polar vectors, which are used to describe magnetic fields and magnetic moments. In fact, magnetic field, ΔH, produced by the element Δlof a conducting wire carrying electric current, I c, is described by the Biot–Savartlaw:
(1.7) 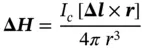
Читать дальше

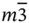 and
and 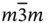 ( Table 1.1). Evidently, the loss of an inversion center can happen in crystals, which are built of several Bravaislattices, their origins being shifted relative to each other. We stress that it is necessary, but not sufficient condition for the loss of inversion center. For illustration, let us consider Si (diamond structure) and GaAs (zinc blende or sphalerite structure) crystals. Both comprise two fcc lattices shifted relative to each other by one quarter of a space cube diagonal. The difference is that in silicon these sub-lattices are occupied by identical atoms (Si), whereas in GaAs – separately by Ga and As. In a result, Si is centro-symmetric (class
( Table 1.1). Evidently, the loss of an inversion center can happen in crystals, which are built of several Bravaislattices, their origins being shifted relative to each other. We stress that it is necessary, but not sufficient condition for the loss of inversion center. For illustration, let us consider Si (diamond structure) and GaAs (zinc blende or sphalerite structure) crystals. Both comprise two fcc lattices shifted relative to each other by one quarter of a space cube diagonal. The difference is that in silicon these sub-lattices are occupied by identical atoms (Si), whereas in GaAs – separately by Ga and As. In a result, Si is centro-symmetric (class 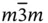 ) that can be easily proved by setting inversion center at point (⅛,⅛,⅛), i.e. in the middle between the origins of two centro-symmetric fcc Si sub-lattices ( Figure 1.11a). This recipe can hardly be used in case of GaAs since there is no symmetry operation that converts Ga to As ( Figure 1.11b). Therefore, GaAs is non-centro-symmetric crystal belonging to class
) that can be easily proved by setting inversion center at point (⅛,⅛,⅛), i.e. in the middle between the origins of two centro-symmetric fcc Si sub-lattices ( Figure 1.11a). This recipe can hardly be used in case of GaAs since there is no symmetry operation that converts Ga to As ( Figure 1.11b). Therefore, GaAs is non-centro-symmetric crystal belonging to class 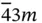 and revealing significant piezoelectric effect.
and revealing significant piezoelectric effect.

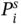 , in ferroelectric crystals (see Chapter 12). Spontaneous polarization, as well as polarization, P i, induced by external electric field, is defined as the sum of elementary dipole moments per unit volume. Note that polarization Pis polar vector having three projections, P i, as e.g. radius-vector r(with projections, x i). There exist also axial vectors (or pseudo-vectors), i.e. vector products (cross products) of polar vectors, which are used to describe magnetic fields and magnetic moments. In fact, magnetic field, ΔH, produced by the element Δlof a conducting wire carrying electric current, I c, is described by the Biot–Savartlaw:
, in ferroelectric crystals (see Chapter 12). Spontaneous polarization, as well as polarization, P i, induced by external electric field, is defined as the sum of elementary dipole moments per unit volume. Note that polarization Pis polar vector having three projections, P i, as e.g. radius-vector r(with projections, x i). There exist also axial vectors (or pseudo-vectors), i.e. vector products (cross products) of polar vectors, which are used to describe magnetic fields and magnetic moments. In fact, magnetic field, ΔH, produced by the element Δlof a conducting wire carrying electric current, I c, is described by the Biot–Savartlaw: