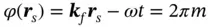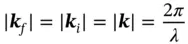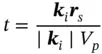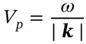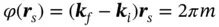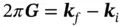(1.20) 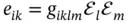
or changes in refractive index, as a function of quadratic form of electric filed, as for quadratic electro-optic effect, r iklm(see Chapter 12):
(1.21) 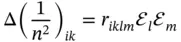
Eqs. (1.20, 1.21)describe the second order (quadratic) effects in the induced strain and change of refractive index, respectively, as a result of electric field application to a crystal. Tensor of rank 4 may also interconnect scalar quantity with two tensors of the second rank, as the stiffness tensor does when one calculates the density of elastic energy, W el, stored within a crystal:
(1.22) 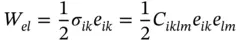
Therefore, using tensor representation of applied stress via induced strain ( Eq. (1.18)), we find the density of elastic energy to be quadratic with respect to the induced strain. Tensors of rank higher than 4 describe high-order effects in the interaction between external fields and materials. These effects are regularly weak and, hence, are not discussed here.
Tensors of different ranks are appropriately transformed under local symmetry operations. All these operations can be exemplified as certain rotations of coordinate system, in which tensors are defined. Transformed tensor forms are compared with the initial ones, and, on this basis, symmetry restrictions on physical properties are imposed, to be in accordance with Neumann's principle. Based on this comparison, the zero tensor components can be determined, as well as symmetry-mediated relationships between non-zero tensor components. More information on symmetry aspects in crystals can be found in the dedicated crystallography books.
Additional interesting and important physical phenomenon, also related to symmetry operations, is twinning in crystals. For example, it stands behind the crystallography of ferroelectric domains (see Chapter 12) and is one of the channels of plastic deformation in crystals being competitive with dislocation glide. We stress that in terms of crystallography, twinning always is the result of symmetry operations, but those not belonging to the point group of a specific crystal. More information about twinning in crystals is given in Appendix 1.B.
1.3 Wave Propagation in Periodic Media and Construction of Reciprocal Lattice
With no doubts, leading crystal symmetry is translational symmetry, which is of great importance to the foundations of solid state physics. In particular, it allows us to deeply understand the essential features of wave propagation in periodic media, which influence a majority of physical phenomena in crystals. We start now with the symmetry-based analysis of wave propagation following the ideas of Leon Brillouin.
Let us consider, first, the propagation of the plane electron wave, Y = Y 0exp[ i ( kr− ωt )], in a homogeneous medium. Here, Y 0is the wave amplitude, kis the wavevector, and ω is the wave angular frequency, whereas rand t are the spatial and temporal coordinates. The phase of plane wave is ϕ = ( kr− ωt ), i.e. Y = Y 0exp( iϕ ). According to the Emmy Noethertheorem, the homogeneity of space leads to the momentum conservation law. It means that an electron wave having wavevector, k i, at a certain point in its trajectory, will continue to propagate with the same wavevector since the wavevector, k, is linearly related to the momentum, P, via the reduced Planckconstant ℏ , i.e. P = ℏ k. The latter relationship follows from the de Brogliedefinition of the particle wavelength ( de Brogliewavelength) via its momentum: 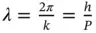 .
.
The situation drastically changes for a non-homogeneous medium, in which the momentum conservation law, generally, is not valid because of the breaking of the aforementioned symmetry (homogeneity of space). Consequently, in such a medium, one can find wavevectors, k f, differing from the initial wavevector, k i.
Our focus here is on a non-homogeneous medium with translational symmetry, which comprises scattering centers in specific points, r s, given by Eq. (1.1). Based on the translational symmetry only, we can say that in an infinite medium with no absorption, the magnitude of plane wave, Y , should be the same near each lattice node. It means that the amplitude, Y 0, is the same at all points, r s, whereas the phase, ϕ = kr− ωt , can differ by an integer number m of 2 π .Let us suppose that the plane wave has wavevector, k i, at starting point r 0= 0 and time moment, t 0= 0, and hence ϕ (0) = 0. If so, at point r s, the phase, ϕ ( r s), should be equal:
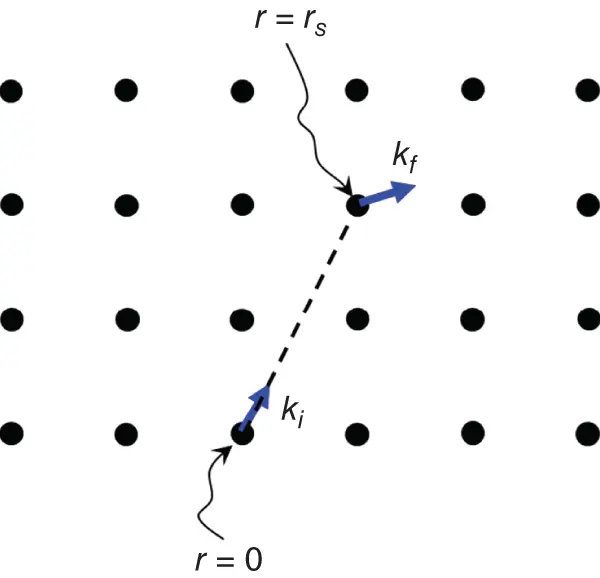
Figure 1.13Illustration of the wave scattering in a periodic medium.
(1.23) 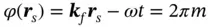
Note that the change of the wavevector from k ito k fphysically means that the wave experiences scattering in point, r s( Figure 1.13). For elastic scattering (with no energy change):
(1.24) 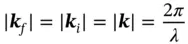
where λ is the electron wavelength. Furthermore, the time interval, t , for wave propagation between points, r 0= 0 and r s, equals
(1.25) 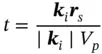
where
(1.26) 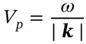
is the phase wave velocity. Substituting Eqs. (1.24— 1.26)into Eq. (1.23)yields:
(1.27) 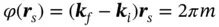
Introducing a new vector, G, which is called vector of reciprocal lattice,
(1.28) 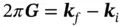
Читать дальше

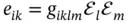
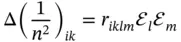
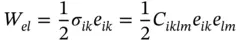
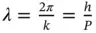 .
.