In fact, it follows from triangle DOB that DB = 2⋅DO⋅sin( δ /2). The plane of triangle DAB is perpendicular to the axis OA and hence the angle ∠ OAD = 90°. If so, DA = DO⋅sin δ and from triangle DAB, the segment DB = 2⋅DA⋅sin( φ /2) = 2⋅DO⋅sin( φ /2)⋅sin δ . Comparing two expressions for segment DB, given in this paragraph, yields  , or
, or
(1.A.2) 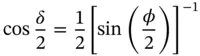
For a threefold rotation axis (axis 3 , φ = 120°), Eq. (1.A.2)predicts that 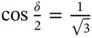 and, correspondingly, cos δ = −1/3. This angle, δ = 109.47°, is between the space cube diagonals, e.g. between the [111]- and [
and, correspondingly, cos δ = −1/3. This angle, δ = 109.47°, is between the space cube diagonals, e.g. between the [111]- and [ 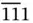 ]-diagonals. In other words, crystal symmetry permits the existence of single axis 3 , as follows from translational symmetry, or the simultaneous existence of four such axes (no more, not less), arranged in 3D space as spatial diagonals of a cube. The arrangement of four threefold rotation axes is the leading combination in the cubic symmetry system, existing in all five its classes (point groups) ( Table 1.1).
]-diagonals. In other words, crystal symmetry permits the existence of single axis 3 , as follows from translational symmetry, or the simultaneous existence of four such axes (no more, not less), arranged in 3D space as spatial diagonals of a cube. The arrangement of four threefold rotation axes is the leading combination in the cubic symmetry system, existing in all five its classes (point groups) ( Table 1.1).
For a fourfold rotation axis ( 4, φ = 90°), Eq. (1.A.2)gives cos  , i.e. δ = 90°. This is the angle between cube edges. In other words, crystal symmetry permits the existence of single axis 4 , or three such axes, arranged as cube edges, i.e. with angles δ = 90° between them. This combination exists in classes 432 and
, i.e. δ = 90°. This is the angle between cube edges. In other words, crystal symmetry permits the existence of single axis 4 , or three such axes, arranged as cube edges, i.e. with angles δ = 90° between them. This combination exists in classes 432 and  of the cubic symmetry system ( Table 1.1). In cubic class
of the cubic symmetry system ( Table 1.1). In cubic class 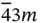 , we find three fourfold roto-inversion axes, which combine 90° rotation followed by inversion operation.
, we find three fourfold roto-inversion axes, which combine 90° rotation followed by inversion operation.
For a sixfold rotation axis ( 6 , φ = 60°), Eq. (1.A.2)yields cos( δ /2) = 1, i.e. δ = 0. In other words, crystal symmetry allows the existence of single sixfold axis only in all classes of hexagonal symmetry ( Table 1.1).
As was already mentioned, twinning is very interesting and practically important phenomenon in crystal physics, which is tightly related to specific symmetry operations. The phenomenon of twinning in crystals has been extensively studied due to its emergence in crystal growth and phase transformations and its substantial effect on mechanical, electrical, and optical properties in real crystals. In fact, twinning is one of the key mechanisms of plastic deformation in metals and ceramics. Quite often it serves as a structural basis for different types of ferroelectric domains (see Chapter 12) or structural variants in shape-memory alloys.
In contrast to what we have learned until now, symmetry operations involved into twinning processes are not included into the point group of a particular crystal, in which twinning occurs. Correspondingly, twins are crystal parts (sometimes called individuals), which are transformed into each other under such symmetry operations. In fact, if a specific symmetry element, considered for twinning, belongs to the crystal point group, its application to one crystal part would produce perfect continuation of the crystal, rather than a twin. In principle, every basic symmetry element, introduced earlier in Section 1.1, may serve for twinning, if it does not belong to the point group set for a given crystal. However, most frequently twins are produced by reflection in a mirror plane or by a 180° rotation about the twofold rotation axis perpendicular to the boundary plane between the twinned parts. If a crystal has an inversion center, both operations result in identical twins.
Let us illustrate these considerations by two examples, the first being taken for monoclinic lattice, which is characterized by lattice translations a, b, and cand angle γ ≠ 90° between vectors aand b. Correspondingly, vector cis perpendicular to both the vectors aand b. In monoclinic crystals, containing mirror plane as symmetry element (classes m and 2/m , see Table 1.1), this plane is horizontal, i.e. perpendicular to the c-translation (in our setting). Consequently, the planes containing translations aand cor band care not mirror planes ( Figure 1.19). However, if nevertheless, part of the crystal is produced according to this “forbidden” symmetry operation (as fault during growth or because of stress application), one obtains twins shown in Figure 1.19. The angle between twinned parts equals 180° – 2 γ .
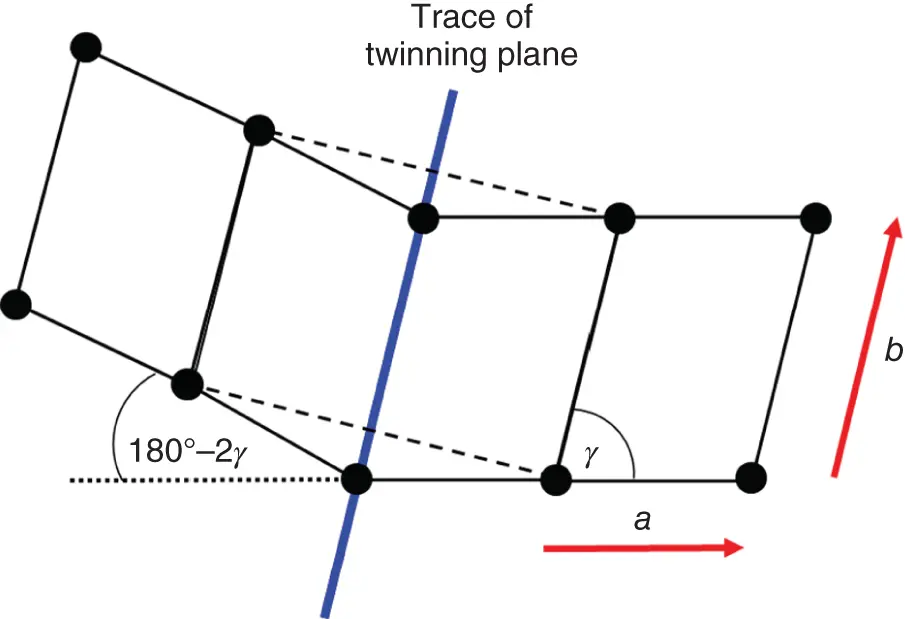
Figure 1.19Illustration of twin formation in monoclinic lattice via mirror reflection in plane containing the b- and c-translations. The latter is perpendicular to the plane of drawing. The a- and b-translation vectors are indicated by red arrows. Twins are crystal parts located at right-hand and left-hand sides from the trace of the twinning plane (blue solid line).
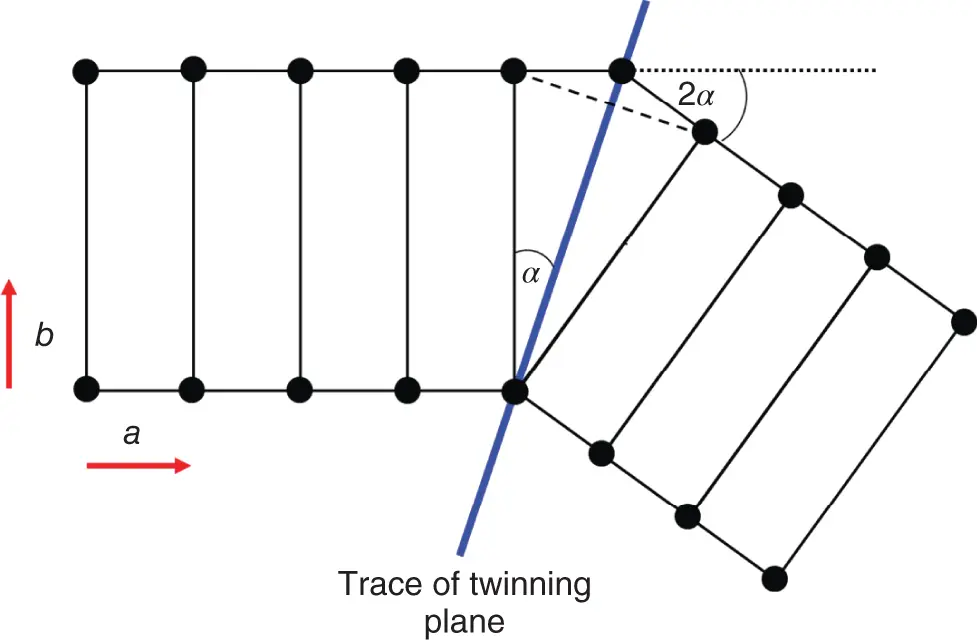
Figure 1.20Illustration of twin formation in orthorhombic lattice via mirror reflection in plane containing the ( b+ a)- and c-translations. The latter is perpendicular to the plane of drawing. The a- and b-translation vectors are indicated by red arrows. Twins are crystal parts located at right-hand and left-hand sides from the trace of the twinning plane (blue solid line).
As second example, let us consider orthorhombic lattice with lattice translations a, b, c, being mutually perpendicular to each other. In orthorhombic crystals (classes 222 , mm2 , and mmm , see Table 1.1), the faces of rectangular prism, which represents unit cell, are related to certain symmetry elements. For class mm2 they are mirror planes, while for class 222 the normals to these planes are the twofold rotation axes. For class mmm both assertions are valid. Therefore, if we apply these symmetry operations to one part of the respective crystal, we will obtain its perfect continuation. Situation is changed, if we consider mirror plane, which contains one of the face diagonals of the prism as well as translation vector situated normally to the face chosen. This geometry is shown in Figure 1.20 ,for mirror plane, which contains vectors a+ b(as face diagonal) and vector c. Application of such mirror plane to a part of the crystal produces twin as is clearly seen in Figure 1.20. If the angle between vector band the trace of the twinning plane equals α , then the angle between twinned parts is 2 α .
Читать дальше

 , or
, or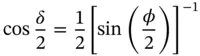
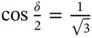 and, correspondingly, cos δ = −1/3. This angle, δ = 109.47°, is between the space cube diagonals, e.g. between the [111]- and [
and, correspondingly, cos δ = −1/3. This angle, δ = 109.47°, is between the space cube diagonals, e.g. between the [111]- and [ 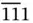 ]-diagonals. In other words, crystal symmetry permits the existence of single axis 3 , as follows from translational symmetry, or the simultaneous existence of four such axes (no more, not less), arranged in 3D space as spatial diagonals of a cube. The arrangement of four threefold rotation axes is the leading combination in the cubic symmetry system, existing in all five its classes (point groups) ( Table 1.1).
]-diagonals. In other words, crystal symmetry permits the existence of single axis 3 , as follows from translational symmetry, or the simultaneous existence of four such axes (no more, not less), arranged in 3D space as spatial diagonals of a cube. The arrangement of four threefold rotation axes is the leading combination in the cubic symmetry system, existing in all five its classes (point groups) ( Table 1.1). , i.e. δ = 90°. This is the angle between cube edges. In other words, crystal symmetry permits the existence of single axis 4 , or three such axes, arranged as cube edges, i.e. with angles δ = 90° between them. This combination exists in classes 432 and
, i.e. δ = 90°. This is the angle between cube edges. In other words, crystal symmetry permits the existence of single axis 4 , or three such axes, arranged as cube edges, i.e. with angles δ = 90° between them. This combination exists in classes 432 and  of the cubic symmetry system ( Table 1.1). In cubic class
of the cubic symmetry system ( Table 1.1). In cubic class 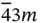 , we find three fourfold roto-inversion axes, which combine 90° rotation followed by inversion operation.
, we find three fourfold roto-inversion axes, which combine 90° rotation followed by inversion operation.












