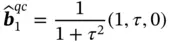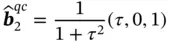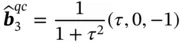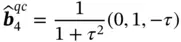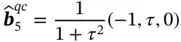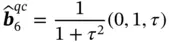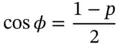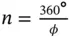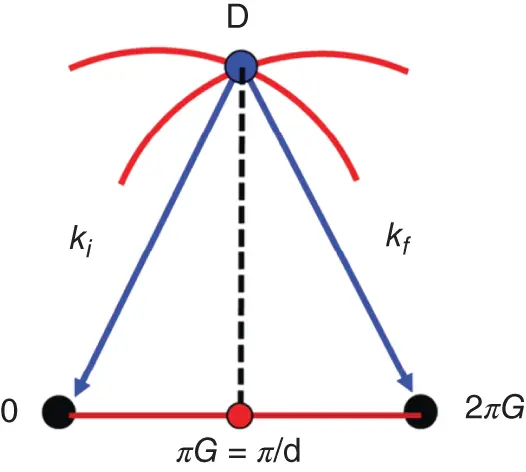
Figure 1.16The traces of isoenergetic surfaces (red curves) in reciprocal space for the incident ( k i) and diffracted ( k f) waves. The point of degeneracy of quantum states is marked by the letter D.
where G 0is some constant and 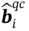 are unit vectors expressed via the golden ratio ( Eq. (1.6)), as:
are unit vectors expressed via the golden ratio ( Eq. (1.6)), as:
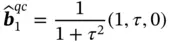
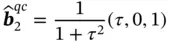
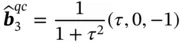
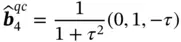
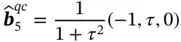
(1.42) 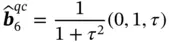
Using this terminology, regular crystals constitute the largest class, for which n = 3 (see Eq. (1.36)).
Considering the latter, we stress that in an infinite periodic medium, the waves having wavevectors k iand k f= k i+ 2 πG are identical from quantum-mechanical point of view that leads to the degeneracy of the corresponding quantum states. The degeneracy point (marked by letter D in Figure 1.16) is located at the intersection of the iso-energetic surfaces (red lines in Figure 1.16) for the incident ( k i) and diffracted ( k f) waves. Being projected onto vector Gin reciprocal space, this point called as the Brillouinzone boundary is in the middle between the 0and G-nodes of the reciprocal lattice ( Figure 1.16). Construction based on lines and surfaces normally cutting corresponding vectors of reciprocal lattices in their middles is used to build Brillouinzones in two and three dimensions (see Chapter 2). As we also will see in Chapter 2, the degeneracy of states at the Brillouinzone boundary is removed by an interaction of electron waves with periodic lattice potential that results in the formation of the forbidden energy zones (gaps). Within these gaps, the electron states do not exist. Therefore, we can say that energy gaps in crystals are formed due to diffraction of free (or almost free) valence electrons, having wavevectors comparable with vectors of reciprocal lattice.
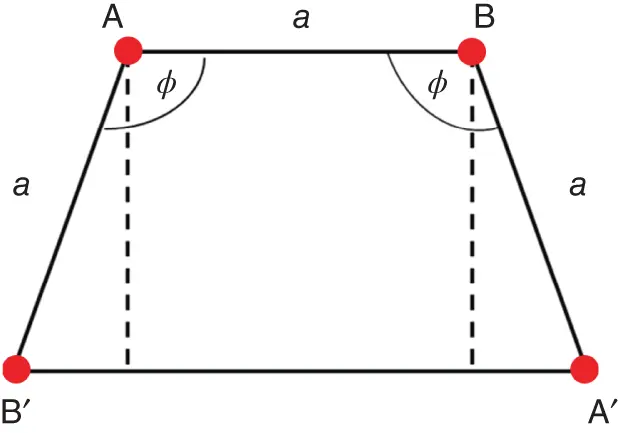
Figure 1.17Illustration of the restrictions imposed by translational symmetry on permitted types of rotation axes in crystals.
1.A Symmetry Constraints on Rotation Axes
As was already mentioned, translational symmetry imposes tight constraints on possible kinds of rotation axes in crystals. This is one of the strongest and most important results in crystallography. In fact, let us consider the network of equivalent points in space, which are related to each other by translational symmetry (i.e. are produced from some origin by linear combinations of translation vectors, see Eq. (1.1)). Suppose that the rotation axis, which is characterized by the elementary rotation angle φ , crosses one of these points (say point A), perpendicularly to the plane of drawing ( Figure 1.17). Point B is shifted from point A by translation vector a, the distance AB being equal to the translation length, a . Since point B belongs to the same network, the identical rotation axis is passing also through it. Let rotate point B by angle φ about the axis passing through point A. In such a way, we receive third equivalent point B′. Repeating this procedure for point A (i.e. rotating it by angle φ about the axis passing through point B), we obtain fourth equivalent point A′. Being equivalent, all four points belong to the same network. It means that the distance A′B′ should be an integer number of translations, a (since vector A′ B′ is parallel to vector AB = a), i.e. A′B′ = pa , where p is an integer. On the other hand, by considering the geometry in Figure 1.17, one finds that A′B′ = AB + 2AB′ · sin ( φ −90°). Using AB = AB′ = a yields pa = a + 2 a· sin( φ −90°), and finally:
(1.A.1) 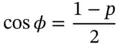
Restrictions imposed on possible types of rotation axes by Eq. (1.A.1), mathematically follow from two conditions: |cos φ | ≤ 1 and integer numbers of p . Possible values of cos φ and p , as well as the order of the axis, n = 360°/ φ , are given in Table 1.2.
First numerical line in Table 1.2contains trivial symmetry element, i.e. rotation axis 1 ( n = 1, φ = 360°). It is trivial since each geometrical figure transforms into itself under rotation by 360°. According to Table 1.2, as non-trivial elements, there are only four different rotation axes in crystals, which are compatible with translational symmetry: 2 ( n = 2, φ = 180°), 3 ( n = 3, φ = 120°), 4 ( n = 4, φ = 90°), and 6 ( n = 6, φ = 60°).
As next important question, we ask: how many rotation axes of the same high order ( 3 , 4 , or 6 ) can simultaneously exist in a crystal? To address it, let take one n -fold axis, marked as OA in Figure 1.18, and add to it another axis of this kind (OB) inclined by angle δ . Then, we can rotate the axis OB around OA by the elementary rotation angle, φ = 360°/ n , and produce the third axis, OD. The duplication procedure can be continued. However, all these axes are equivalent and, thus, the angles between them should be equal δ . The latter condition imposes strong restrictions on possible configurations of equivalent rotation axes in crystals and angles between them.
Table 1.2Possible types of rotation axes permitted by translational symmetry.
| p |
cos φ |
φ |
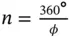 |
| −1 |
1 |
360° |
1 |
| 0 |
½ |
60° |
6 |
| 1 |
0 |
90° |
4 |
| 2 |
−½ |
120° |
3 |
| 3 |
−1 |
180° |
2 |
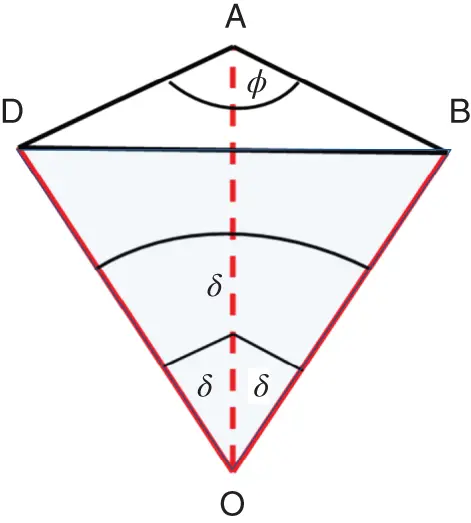
Figure 1.18Illustration of the simultaneous appearance of several high-order rotation axes in a crystal.
Читать дальше


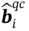 are unit vectors expressed via the golden ratio ( Eq. (1.6)), as:
are unit vectors expressed via the golden ratio ( Eq. (1.6)), as: