1 ...8 9 10 12 13 14 ...19 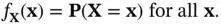
Definition 2.21 (Probability density function)The pdf, 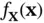 of a continuous random variable
of a continuous random variable 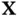 is the function that satisfies
is the function that satisfies
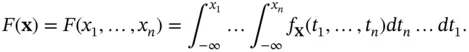
We will discuss these notations in details in Chapter 20.
Using these concepts, we can define the moments of the distribution. In fact, suppose that 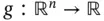 is any function, then we can calculate the expected value of the random variable
is any function, then we can calculate the expected value of the random variable  when the joint density exists as:
when the joint density exists as:
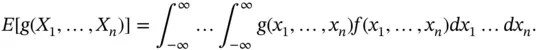
Now we can define the moments of the random vector. The first moment is a vector
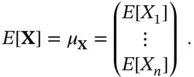
The expectation applies to each component in the random vector. Expectations of functions of random vectors are computed just as with univariate random variables. We recall that expectation of a random variable is its average value.
The second moment requires calculating all the combination of the components. The result can be presented in a matrix form. The second central moment can be presented as the covariance matrix.
(2.1) 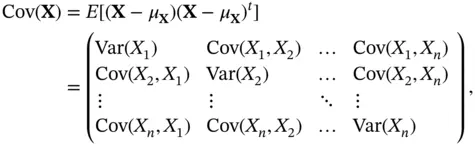
where we used the transpose matrix notation and since the 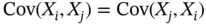 , the matrix is symmetric.
, the matrix is symmetric.
We note that the covariance matrix is positive semidefinite (nonnegative definite), i.e. for any vector  , we have
, we have 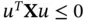 .
.
Now we explain why the covariance matrix has to be semidefinite. Take any vector  . Then the product
. Then the product
(2.2) 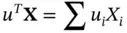
is a random variable (one dimensional) and its variance must be nonnegative. This is because in the one‐dimensional case, the variance of a random variable is defined as 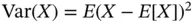 . We see that the variance is nonnegative for every random variable, and it is equal to zero if and only if the random variable is constant. The expectation of ( 2.2) is
. We see that the variance is nonnegative for every random variable, and it is equal to zero if and only if the random variable is constant. The expectation of ( 2.2) is  . Then we can write (since for any number
. Then we can write (since for any number 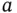 ,
, 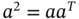 )
)
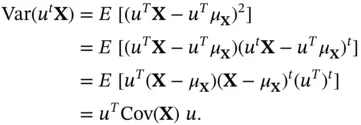
Since the variance is always nonnegative, the covariance matrix must be nonnegative definite (or positive semidefinite). We recall that a square symmetric matrix  is positive semidefinite if
is positive semidefinite if 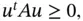
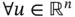 . This difference is in fact important in the context of random variables since you may be able to construct a linear combination
. This difference is in fact important in the context of random variables since you may be able to construct a linear combination 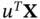 which is not always constant but whose variance is equal to zero.
which is not always constant but whose variance is equal to zero.
The covariance matrix is discussed in detail in Chapter 3.
We now present examples of multivariate distributions.
2.3.1 The Dirichlet Distribution
Before we discuss the Dirichlet distribution, we define the Beta distribution.
Definition 2.22 (Beta distribution)A random variable 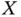 is said to have a Beta distribution with parameters
is said to have a Beta distribution with parameters  and
and 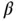 if it has a pdf
if it has a pdf 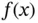 defined as:
defined as:
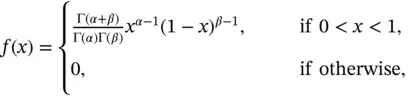
where 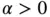 and
and 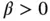 .
.
The Dirichlet distribution 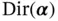 , named after Johann Peter Gustav Lejeune Dirichlet (1805–1859), is a multivariate distribution parameterized by a vector
, named after Johann Peter Gustav Lejeune Dirichlet (1805–1859), is a multivariate distribution parameterized by a vector 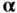 of positive parameters
of positive parameters 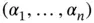 .
.
Читать дальше

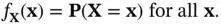
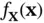 of a continuous random variable
of a continuous random variable 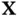 is the function that satisfies
is the function that satisfies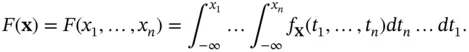
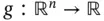 is any function, then we can calculate the expected value of the random variable
is any function, then we can calculate the expected value of the random variable  when the joint density exists as:
when the joint density exists as: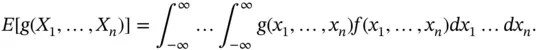
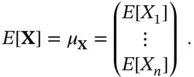
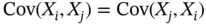 , the matrix is symmetric.
, the matrix is symmetric. , we have
, we have 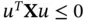 .
. . Then the product
. Then the product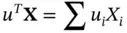
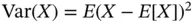 . We see that the variance is nonnegative for every random variable, and it is equal to zero if and only if the random variable is constant. The expectation of ( 2.2) is
. We see that the variance is nonnegative for every random variable, and it is equal to zero if and only if the random variable is constant. The expectation of ( 2.2) is  . Then we can write (since for any number
. Then we can write (since for any number 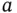 ,
, 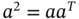 )
)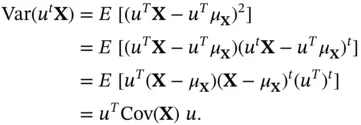
 is positive semidefinite if
is positive semidefinite if 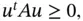
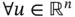 . This difference is in fact important in the context of random variables since you may be able to construct a linear combination
. This difference is in fact important in the context of random variables since you may be able to construct a linear combination 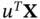 which is not always constant but whose variance is equal to zero.
which is not always constant but whose variance is equal to zero.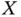 is said to have a Beta distribution with parameters
is said to have a Beta distribution with parameters 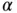 and
and 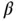 if it has a pdf
if it has a pdf 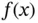 defined as:
defined as: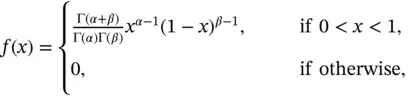
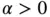 and
and 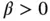 .
.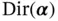 , named after Johann Peter Gustav Lejeune Dirichlet (1805–1859), is a multivariate distribution parameterized by a vector
, named after Johann Peter Gustav Lejeune Dirichlet (1805–1859), is a multivariate distribution parameterized by a vector 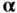 of positive parameters
of positive parameters 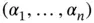 .
.
![Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]](/books/438007/roman-zykov-roman-s-data-science-kak-monetizirova-thumb.webp)









