Maria Cristina Mariani - Data Science in Theory and Practice
Здесь есть возможность читать онлайн «Maria Cristina Mariani - Data Science in Theory and Practice» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Data Science in Theory and Practice
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Data Science in Theory and Practice: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Data Science in Theory and Practice»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
will also earn a place in the libraries of practicing data scientists, data and business analysts, and statisticians in the private sector, government, and academia.

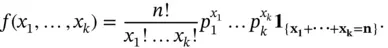
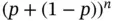 , the multinomial probabilities are the coefficients in the multinomial expansion
, the multinomial probabilities are the coefficients in the multinomial expansion  , so they sum to 1. This expansion in fact gives the name of the distribution.
, so they sum to 1. This expansion in fact gives the name of the distribution.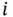 as a success and everything else a failure, then
as a success and everything else a failure, then  simply counts successes in
simply counts successes in 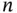 independent trials and thus
independent trials and thus 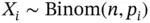 . Thus, the first moment of the random vector and the diagonal elements in the covariance matrix are easy to calculate as
. Thus, the first moment of the random vector and the diagonal elements in the covariance matrix are easy to calculate as  and
and 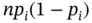 , respectively. The off‐diagonal elements (covariances) are not that complicated to calculate either. However, for multinomial random vectors, the first two moments are difficult to compute. The one‐dimensional marginal distributions are binomial; however, the joint distribution of
, respectively. The off‐diagonal elements (covariances) are not that complicated to calculate either. However, for multinomial random vectors, the first two moments are difficult to compute. The one‐dimensional marginal distributions are binomial; however, the joint distribution of  , the first
, the first 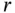 components, is not multinomial. Instead, suppose we group the first
components, is not multinomial. Instead, suppose we group the first 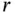 categories into 1 and we let
categories into 1 and we let 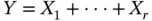 . Because the categories are linked, that is,
. Because the categories are linked, that is, 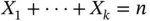 , we also have that
, we also have that 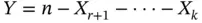 . We can easily verify that the vector
. We can easily verify that the vector 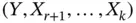 , or equivalently
, or equivalently 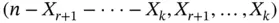 , will have a multinomial distribution with associated probabilities
, will have a multinomial distribution with associated probabilities 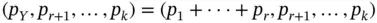 .
.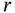 components given the last
components given the last 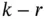 components. That is, the distribution of
components. That is, the distribution of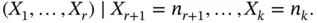
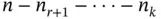 and probabilities
and probabilities  , where
, where 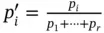 .
.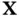 is said to have a
is said to have a 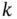 ‐dimensional multivariate normal distribution (denoted
‐dimensional multivariate normal distribution (denoted 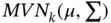 , where
, where 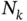 is
is 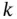 ‐dimensional multivariate normal distribution) with mean vector
‐dimensional multivariate normal distribution) with mean vector 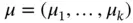 and covariance matrix
and covariance matrix 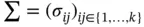 if its density can be written as
if its density can be written as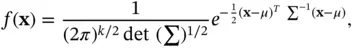
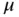 may have any elements in
may have any elements in 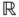 , but, just as in the one‐dimensional case, the standard deviation has to be positive. In the multivariate case, the covariance matrix
, but, just as in the one‐dimensional case, the standard deviation has to be positive. In the multivariate case, the covariance matrix  has to be symmetric and positive definite.
has to be symmetric and positive definite.
![Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]](/books/438007/roman-zykov-roman-s-data-science-kak-monetizirova-thumb.webp)









