Maria Cristina Mariani - Data Science in Theory and Practice
Здесь есть возможность читать онлайн «Maria Cristina Mariani - Data Science in Theory and Practice» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Data Science in Theory and Practice
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Data Science in Theory and Practice: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Data Science in Theory and Practice»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
will also earn a place in the libraries of practicing data scientists, data and business analysts, and statisticians in the private sector, government, and academia.

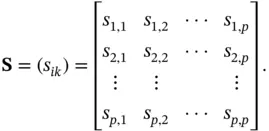
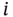 th and
th and 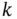 th variables,
th variables, 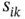 , is calculated using the
, is calculated using the 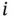 th and
th and 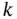 th columns of
th columns of 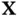 :
: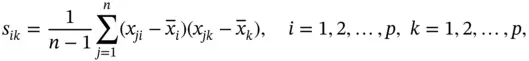
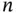 is the number of measurements.
is the number of measurements.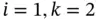 :
: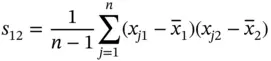
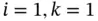 :
: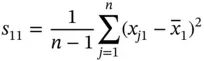
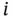 th and
th and 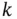 th variables. The sample covariance reduces to the sample variance when
th variables. The sample covariance reduces to the sample variance when 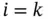 as observed in ( 3.4). We note that the sample covariance matrix ( 3.1) is symmetric, i.e.
as observed in ( 3.4). We note that the sample covariance matrix ( 3.1) is symmetric, i.e. 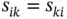 for all
for all 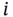 and
and 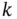 because of its definition. Other names used for the covariance matrix are variance matrix, variance–covariance matrix, and dispersion matrix. In finance the concept of covariance is applied in portfolio theory, in the diversification method, that reduces the risk by choosing assets that do not present a high positive covariance with each other.
because of its definition. Other names used for the covariance matrix are variance matrix, variance–covariance matrix, and dispersion matrix. In finance the concept of covariance is applied in portfolio theory, in the diversification method, that reduces the risk by choosing assets that do not present a high positive covariance with each other.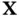 is a random vector taking on any possible value in a multivariate population, the population covariance matrixis defined as
is a random vector taking on any possible value in a multivariate population, the population covariance matrixis defined as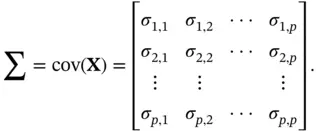
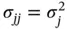 are the population variances of the
are the population variances of the 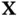 's, and the off‐diagonal elements
's, and the off‐diagonal elements 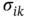 are the population covariances of all possible pairs of
are the population covariances of all possible pairs of 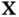 s, i.e.
s, i.e. 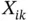 for
for 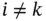 .
.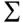 for the covariance matrix is widely used and seems natural because
for the covariance matrix is widely used and seems natural because 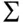 is the uppercase version of
is the uppercase version of 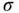 .
.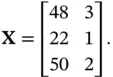
 as follows:
as follows: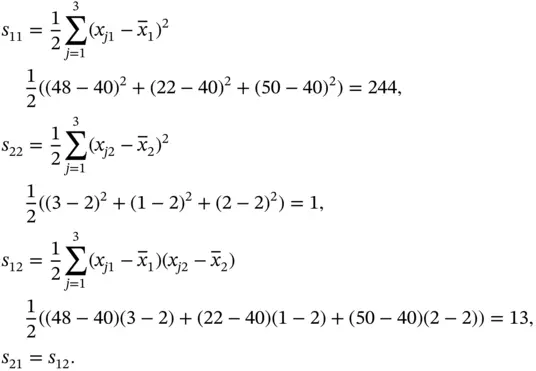
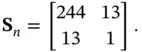
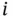 th and
th and 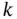 th variables is defined as
th variables is defined as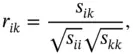

![Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]](/books/438007/roman-zykov-roman-s-data-science-kak-monetizirova-thumb.webp)









