where
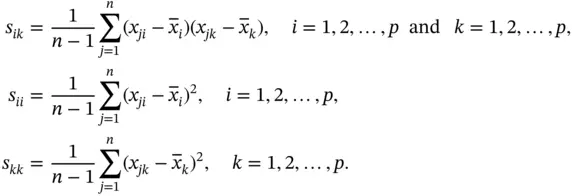
Substituting 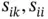 and
and 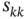 into ( 3.6) and canceling terms, we obtain
into ( 3.6) and canceling terms, we obtain
(3.7) 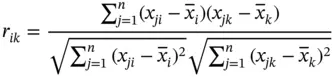
for 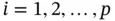 and
and 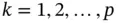 . We note that the sample correlation is symmetric since
. We note that the sample correlation is symmetric since 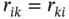 for all
for all 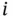 and
and 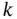 .
.
The sample correlation coefficient is a measure of the linear association between two variables and does not depend on the units of measurement, i.e. when you construct the sample correlation coefficient, the units of measurement that are used cancel out. The sample correlation matrixis analogous to the covariance matrix with correlations in place of covariances:
(3.8) 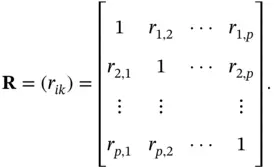
The population correlation matrixsimilar to ( 3.8) is defined as follows:
(3.9) 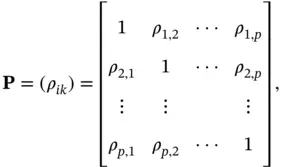
where
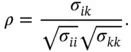
We note that even though the signs of the sample correlation and the sample covariance are the same, the correlation is easier to interpret because its magnitude is bounded. It is bounded within the closed interval 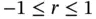 . To summarize, the sample correlation
. To summarize, the sample correlation 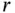 has the following properties:
has the following properties:
1 The value of the sample correlation must lie between and inclusive. indicates perfect linear relationship and indicates perfect inverse relationship.
2 The sample correlation measures the strength of the linear association between two variables. If equals to zero, it implies no linear association between the components. Otherwise, the sign of indicates the direction of the association. If is positive, it means that as one variable gets larger the other gets larger. If is negative, it means that as one gets larger, the other gets smaller (often called an “inverse” correlation). A larger value of implies greater linear strength. This is an indication that both variables move in the opposite direction if one variable increases, the other variable decreases with the same magnitude (and vice versa).
Example 3.4Consider the following data matrix introduced in Example 3.1:
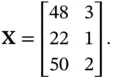
Each receipt yields a pair of measurements, total dollar sales, and number of movies sold. We find the sample correlation  as follows:
as follows:

Therefore,

In this example, we observe the variables 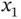 and
and 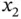 are highly positively correlated since
are highly positively correlated since  . This implies that if dollar sales (
. This implies that if dollar sales ( 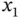 ) increases, the number of movies sold (
) increases, the number of movies sold ( 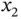 ) also increases.
) also increases.
3.6 Linear Combinations of Variables
Most often, we are interested in linear combinations of the variables 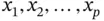 . In this section, we investigate the means, variances, and covariances of linear combinations.
. In this section, we investigate the means, variances, and covariances of linear combinations.
Let 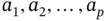 be constants and consider the linear combination of the elements of the vector
be constants and consider the linear combination of the elements of the vector 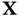 ,
,
(3.10) 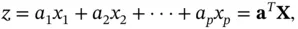
where 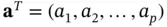 . If the same coefficient vector
. If the same coefficient vector  is applied to each
is applied to each 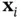 in a sample, we have
in a sample, we have
(3.11) 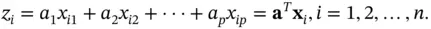
For example, if 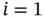 , we have
, we have
Читать дальше

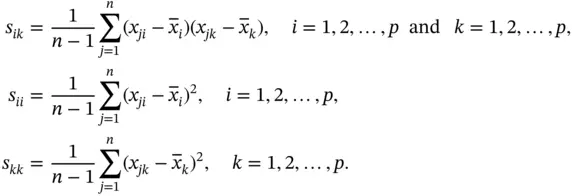
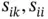 and
and 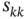 into ( 3.6) and canceling terms, we obtain
into ( 3.6) and canceling terms, we obtain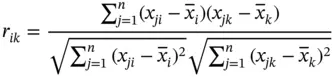
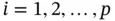 and
and 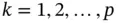 . We note that the sample correlation is symmetric since
. We note that the sample correlation is symmetric since 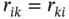 for all
for all 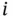 and
and  .
.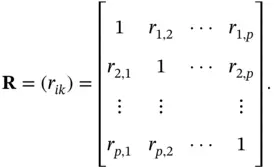
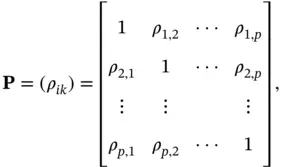
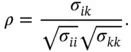
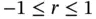 . To summarize, the sample correlation
. To summarize, the sample correlation 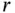 has the following properties:
has the following properties: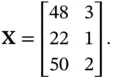
 as follows:
as follows:

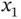 and
and 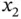 are highly positively correlated since
are highly positively correlated since  . This implies that if dollar sales (
. This implies that if dollar sales ( 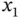 ) increases, the number of movies sold (
) increases, the number of movies sold ( 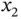 ) also increases.
) also increases.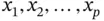 . In this section, we investigate the means, variances, and covariances of linear combinations.
. In this section, we investigate the means, variances, and covariances of linear combinations.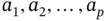 be constants and consider the linear combination of the elements of the vector
be constants and consider the linear combination of the elements of the vector 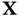 ,
,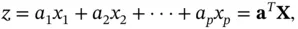
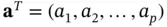 . If the same coefficient vector
. If the same coefficient vector  is applied to each
is applied to each 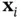 in a sample, we have
in a sample, we have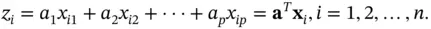
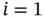 , we have
, we have
![Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]](/books/438007/roman-zykov-roman-s-data-science-kak-monetizirova-thumb.webp)









