The multivariate normal defined thus has many nice properties. The basic one is that the one‐dimensional distributions are all normal, that is, 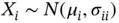 and
and 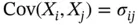 . This is also true for any marginal. For example, if
. This is also true for any marginal. For example, if 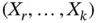 are the last coordinates, then
are the last coordinates, then
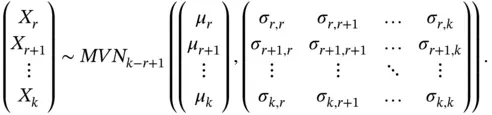
So any particular vector of components is normal.
Conditional distribution of a multivariate normal is also a multivariate normal. Given that 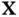 is a
is a 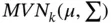 and using the vector notations above assuming that
and using the vector notations above assuming that 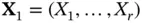 and
and 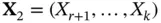 , then we can write the vector
, then we can write the vector 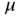 and matrix
and matrix 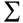 as
as
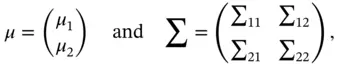
where the dimensions are accordingly chosen to match the two vectors ( 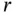 and
and 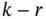 ). Thus, the conditional distribution of
). Thus, the conditional distribution of 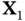 given
given 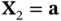 , for some vector
, for some vector 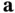 is
is
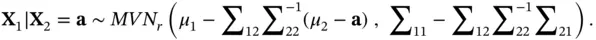
Furthermore, the vectors 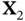 and
and 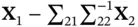 are independent. Finally, any affine transformation
are independent. Finally, any affine transformation 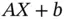 , where
, where 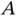 is a
is a 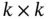 matrix and
matrix and 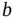 is a
is a 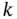 ‐dimensional constant vector, is also a multivariate normal with mean vector
‐dimensional constant vector, is also a multivariate normal with mean vector 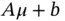 and covariance matrix
and covariance matrix 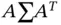 . Please refer to the text by Axler (2015) and Johnson and Wichern (2014) for more details on the Multinomial distribution and Multivariate normal distributions.
. Please refer to the text by Axler (2015) and Johnson and Wichern (2014) for more details on the Multinomial distribution and Multivariate normal distributions.
1 If and are two matrices, prove the following properties of the trace of a matrix..., for a any constant .
2 If and are two matrices, prove the following properties of the determinant of a matrix.det = det .det = det det = det .
3 LetFind .Find .Find .Find .
4 LetFind .Find .Compare and .
5 LetFind .Find .
6 Show that the real symmetric matrixis positive definite for any non‐zero column vector.
7 Prove that if and are positive definite matrices then so is .
8 For what values of is the following matrix positive semidefinite?
9 Decide whether the following matrices are positive definite, negative definite, or neither. Please explain your reasoning.
10 For random variables and , show thatThe variance is the variance of the random variable , while the same holds for the random variable .
3 Multivariate Analysis
3.1 Introduction
Multivariate analysis is the statistical analysis of several variables at once. This is when multiple measurements are made on each experimental unit, and for which the relationship among multivariate measurements and their structure are important to the experiment's understanding. Experimental units are what you apply the treatments to. Many problems in the analysis of life science are multivariate in nature. However the analysis of large multivariable data sets is a major challenge for many research fields. Applications of multivariate techniques are vast. Some includes behavioral and biological sciences, finance, geophysics, medicine, ecology, and many other fields. The materials in this chapter will form the basis of discussion for what will be discussed later in this text.
3.2 Multivariate Analysis: Overview
We begin with the formal definition of multivariate analysis.
Definition 3.1 (Multivariate analysis)Multivariate analysis consists of a collection of techniques that can be used when several measurements are made on each experimental unit.
These measurements (i.e. data) must frequently be arranged and displayed in various ways. We now discuss the concepts underlying the first steps of data organization.
Multivariate data arise whenever an investigator, practitioner, or researcher seeks to study some physical phenomenon and selects a number 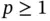 of variables to record. We will use the notation
of variables to record. We will use the notation 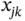 to indicate the particular value of the
to indicate the particular value of the 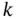 th variable that is observed on the
th variable that is observed on the 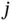 th unit (i.e. subject ). Hence,
th unit (i.e. subject ). Hence, 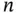 measurements on
measurements on 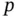 variables can be displayed as a rectangular array called data matrix
variables can be displayed as a rectangular array called data matrix 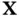 , of
, of 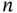 rows and
rows and 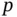 columns:
columns:
Читать дальше

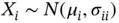 and
and 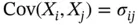 . This is also true for any marginal. For example, if
. This is also true for any marginal. For example, if 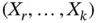 are the last coordinates, then
are the last coordinates, then
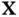 is a
is a 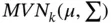 and using the vector notations above assuming that
and using the vector notations above assuming that 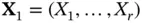 and
and 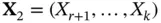 , then we can write the vector
, then we can write the vector 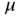 and matrix
and matrix 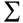 as
as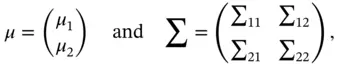
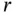 and
and 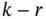 ). Thus, the conditional distribution of
). Thus, the conditional distribution of 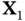 given
given 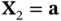 , for some vector
, for some vector 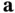 is
is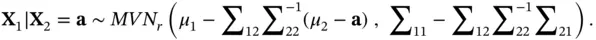
 and
and 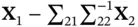 are independent. Finally, any affine transformation
are independent. Finally, any affine transformation 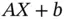 , where
, where 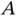 is a
is a 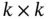 matrix and
matrix and 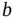 is a
is a 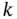 ‐dimensional constant vector, is also a multivariate normal with mean vector
‐dimensional constant vector, is also a multivariate normal with mean vector 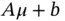 and covariance matrix
and covariance matrix 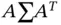 . Please refer to the text by Axler (2015) and Johnson and Wichern (2014) for more details on the Multinomial distribution and Multivariate normal distributions.
. Please refer to the text by Axler (2015) and Johnson and Wichern (2014) for more details on the Multinomial distribution and Multivariate normal distributions.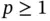 of variables to record. We will use the notation
of variables to record. We will use the notation 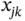 to indicate the particular value of the
to indicate the particular value of the 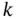 th variable that is observed on the
th variable that is observed on the 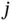 th unit (i.e. subject ). Hence,
th unit (i.e. subject ). Hence, 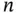 measurements on
measurements on 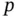 variables can be displayed as a rectangular array called data matrix
variables can be displayed as a rectangular array called data matrix 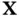 , of
, of 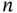 rows and
rows and  columns:
columns:
![Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]](/books/438007/roman-zykov-roman-s-data-science-kak-monetizirova-thumb.webp)









