Iain Pardoe - Applied Regression Modeling

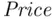Next, to find the probability that a randomly selected is greater than 380, we perform some standard algebra on probability statements. In particular, if we write “the probability that 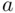is bigger than 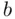” as “ ,” then we can make changes to 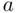(such as adding, subtracting, multiplying, and dividing other quantities) as long as we do the same thing to 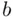. It is perhaps easier to see how this works by example:

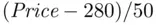The second equality follows since is defined to be 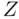, which is a standard normal random variable with mean 0 and standard deviation 1. From the normal table in Section 1.2, the probability that a standard normal random variable is greater than 1.96 is 0.025. Thus, Pr( 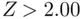) is slightly less than 0.025 (draw a picture of a normal density curve with 1.96 and 2.00 marked on the horizontal axis to convince yourself of this fact). In other words, there is slightly less than a 2.5% chance of finding an expensive home ( 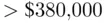) in our housing market, under the assumption that .

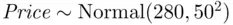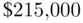For further practice of this kind of calculation, suppose that we have a budget of . What is the probability of finding such an affordable home in our housing market? (You should find it is slightly less than a 10% chance; see Problem 1.10.)

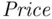We can also turn these calculations around. For example, which value of has a probability of 0.025 to the right of it? To answer this, consider the following calculation: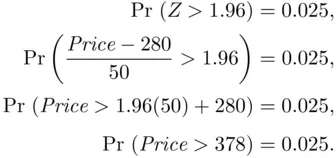

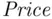So, the value 378 has a probability of 0.025 to the right of it. Another way of expressing this is that “the 97.5th percentile of the variable is .”

In the preceding section, we had to make some pretty restrictive assumptions (normality, known mean, known variance) in order to make statistical inferences. We now explore the connection between samples and populations a little more closely so that we can draw conclusions using fewer assumptions.

Recall that the population is the entire collection of objects under consideration, while the sample is a (random) subset of the population. Sometimes we may have a complete listing of the population (a census), but most of the time a census is too expensive and time consuming to collect. Moreover, it is seldom necessary to consider an entire population in order to make some fairly strong statistical inferences about it using just a random sample.

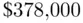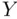We are particularly interested in making statistical inferences not only about values in the population, denoted , but also about numerical summary measures such as the population mean, denoted 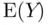—these population summary measures are called parameters . While population parameters are unknown (in the sense that we do not have all the individual population values and so cannot calculate them), we can calculate similar quantities in the sample, such as the sample mean—these sample summary measures are called statistics . (Note the dual use of the term “statistics.” Up until now it has represented the notion of a general methodology for analyzing data based on probability theory, and just now it was used to represent a collection of summary measures calculated from sample data.)

Next we will see how statistical inference essentially involves estimating population parameters (and assessing the precision of those estimates) using sample statistics. When our sample data is a subset of the population that has been selected randomly, statistics calculated from the sample can tell us a great deal about corresponding population parameters. For example, a sample mean tends to be a good estimate of the population mean, in the following sense. If we were to take random samples over and over again, each time calculating a sample mean, then the mean of all these sample means would be equal to the population mean. (There may seem to be a surfeit of “means” in that last sentence, but if you read it slowly enough it will make sense.) Such an estimate is called unbiased since on average it estimates the correct value. It is not actually necessary to take random samples over and over again to show this—probability theory (beyond the scope of this book) allows us to prove such theorems without expending the time and expense of administering a large number of samples.

However, it is not enough to just have sample statistics (such as the sample mean) that average out (over a large number of hypothetical samples) to the correct target (i.e., the population mean). We would also like sample statistics that would have “low” variability from one hypothetical sample to another. At the very least we need to be able to quantify this variability, known as sampling uncertainty. One way to do this is to consider the sampling distribution of a statistic, that is, the distribution of values of a statistic under repeated (hypothetical) samples. Again, we can use results from probability theory to tell us what these sampling distributions are. So, all we need to do is take a single random sample, calculate a statistic, and we will know the theoretical sampling distribution of that statistic (i.e., we will know what the statistic should average out to over repeated samples, and how much the statistic should vary over repeated samples).