| VVHZK |
UHRGF |
HGKDK |
ITKDW |
EFHEV |
SGMPH |
| KIUWA |
XGSQX |
JQHRV |
IUCCB |
GACGF |
SPGLH |
| GFHHD |
MHZGF |
BSPSW |
SDSXR |
DFHEM |
OEPGI |
| QXKZW |
LGHZI |
PHLIV |
VFIPH |
XVA |
|
To find 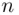 , write the cipher text on a long strip of paper, and copy it onto a second strip of paper beneath the first strip. For a displacement of 1, move the bottom strip to the left by one letter and count the number of character coincidences. Repeat this process for several displacements until the maximum displacement is obtained. The shift shown below corresponds to a displacement of 3:
, write the cipher text on a long strip of paper, and copy it onto a second strip of paper beneath the first strip. For a displacement of 1, move the bottom strip to the left by one letter and count the number of character coincidences. Repeat this process for several displacements until the maximum displacement is obtained. The shift shown below corresponds to a displacement of 3:
|
|
|
V |
V |
H |
Z |
K |
U |
H |
R |
G |
F |
H |
G |
K |
D |
|
 |
 |
| V |
V |
H |
Z |
K |
U |
H |
R |
G |
F |
H |
G |
K |
D |
K |
I |
T |
|
 |
 |
By repeating this process for a number of displacements, we obtain Table 2.2:
Table 2.2Number of character coincidences corresponding to displacement
| Displacement |
Number of coincidences |
| 1 |
4 |
| 2 |
4 |
| 3 |
9 |
| 4 |
12 |
| 5 |
5 |
| 6 |
2 |
| 7 |
7 |
| 8 |
7 |
From our results, the maximum number of occurrences appears for a displacement of 4. Since we know the maximum displacement occurs for a scalar multiple of the period, the period is likely either 2 or 4.
In applying the second principle, we are using a probabilistic argument. That is, in the above example, we cannot be certain that the period is either 2 or 4; however, we can say with high probability that it is likely to be either 2 or 4. If we were unable to decipher the text with a keyword length of 2 or 4, we would then try with the next highest number of coincidences, which occurs for displacement 3.
Now that we know how to find 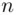 , we examine how to find the keyword itself. Suppose, for example, that the key‐length is 7. Consider the plain text character in the
, we examine how to find the keyword itself. Suppose, for example, that the key‐length is 7. Consider the plain text character in the 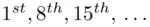 positions (i.e. characters at a distance of 7 spaces). If a particular letter occurs in positions 1 and 8, the cipher text letters in positions 1 and 8 will be the same (because we use the same key letter to encipher both characters). How can we deduce which cipher text characters correspond to which plain text characters? In the English language, the most frequently used letter is “e.” Even if we restrict ourselves to the letters of the message in positions
positions (i.e. characters at a distance of 7 spaces). If a particular letter occurs in positions 1 and 8, the cipher text letters in positions 1 and 8 will be the same (because we use the same key letter to encipher both characters). How can we deduce which cipher text characters correspond to which plain text characters? In the English language, the most frequently used letter is “e.” Even if we restrict ourselves to the letters of the message in positions 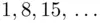 , this will still be the case. Therefore, the most frequent cipher text letter in positions
, this will still be the case. Therefore, the most frequent cipher text letter in positions 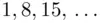 will have come from the enciphering of the letter “e”. Thus, by computing the number of occurrences of each cipher text letter at intervals of 7 letters, we can determine the most frequently occurring cipher text letter and assign it to the plain text letter “e”. Hence, we will have determined the first letter of the keyword. Similar remarks apply to positions {
will have come from the enciphering of the letter “e”. Thus, by computing the number of occurrences of each cipher text letter at intervals of 7 letters, we can determine the most frequently occurring cipher text letter and assign it to the plain text letter “e”. Hence, we will have determined the first letter of the keyword. Similar remarks apply to positions { 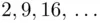 }, {
}, { 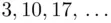 }. In general, if we know the period
}. In general, if we know the period 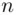 , we can capture the key using frequency analysis.
, we can capture the key using frequency analysis.
We will first try the case where the period is 4, and we will determine the character frequencies for the { 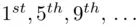 } letters, {
} letters, { 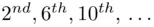 } letters, and so on. Taking the
} letters, and so on. Taking the 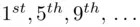 letters, we get
letters, we get
from which we obtain the following table of frequencies:
| A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
| 1 |
0 |
2 |
3 |
1 |
0 |
6 |
0 |
0 |
1 |
2 |
0 |
1 |
| N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
| 0 |
0 |
5 |
0 |
0 |
0 |
1 |
1 |
4 |
0 |
0 |
0 |
0 |
Since G is the most frequently occurring letter, we make the assumption that “e” enciphers to G. Thus the first key letter might be “C.” Similarly, for the second set of letters (i.e. the 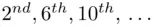 letters), we obtain the following table:
letters), we obtain the following table:
| A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
| 0 |
1 |
0 |
1 |
0 |
5 |
2 |
4 |
2 |
0 |
1 |
0 |
1 |
| N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
| 0 |
1 |
0 |
1 |
0 |
4 |
0 |
1 |
2 |
1 |
0 |
0 |
1 |
Here there are three letters which could likely decipher to “e.” To determine which letter is the right choice, consider each character separately. If “e” enciphers to “F,” we have a key letter of “B.” If “e” enciphers to “H,” we have a key letter of “D.” Finally, if “e” enciphers to “S,” we have a key letter of “O.” Now, we must examine each choice case by case. A key letter of “B” means that the most frequently occurring letters besides “e” are “g” and “r.” Similarly, a key letter of “D” means that the most frequently occurring letters in the plain text (in positions 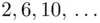 ) besides “e” are “c” and “p.” Finally, a key letter of “O” means that the most frequently occurring letters besides “e” are “t” and “r.”. From the results shown in Table 2.1, it seems that “O” is then the more likely key‐letter. Therefore, we conclude that the second key letter is “O.”
) besides “e” are “c” and “p.” Finally, a key letter of “O” means that the most frequently occurring letters besides “e” are “t” and “r.”. From the results shown in Table 2.1, it seems that “O” is then the more likely key‐letter. Therefore, we conclude that the second key letter is “O.”
Читать дальше

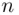 , write the cipher text on a long strip of paper, and copy it onto a second strip of paper beneath the first strip. For a displacement of 1, move the bottom strip to the left by one letter and count the number of character coincidences. Repeat this process for several displacements until the maximum displacement is obtained. The shift shown below corresponds to a displacement of 3:
, write the cipher text on a long strip of paper, and copy it onto a second strip of paper beneath the first strip. For a displacement of 1, move the bottom strip to the left by one letter and count the number of character coincidences. Repeat this process for several displacements until the maximum displacement is obtained. The shift shown below corresponds to a displacement of 3:



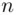 , we examine how to find the keyword itself. Suppose, for example, that the key‐length is 7. Consider the plain text character in the
, we examine how to find the keyword itself. Suppose, for example, that the key‐length is 7. Consider the plain text character in the 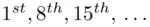 positions (i.e. characters at a distance of 7 spaces). If a particular letter occurs in positions 1 and 8, the cipher text letters in positions 1 and 8 will be the same (because we use the same key letter to encipher both characters). How can we deduce which cipher text characters correspond to which plain text characters? In the English language, the most frequently used letter is “e.” Even if we restrict ourselves to the letters of the message in positions
positions (i.e. characters at a distance of 7 spaces). If a particular letter occurs in positions 1 and 8, the cipher text letters in positions 1 and 8 will be the same (because we use the same key letter to encipher both characters). How can we deduce which cipher text characters correspond to which plain text characters? In the English language, the most frequently used letter is “e.” Even if we restrict ourselves to the letters of the message in positions 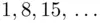 , this will still be the case. Therefore, the most frequent cipher text letter in positions
, this will still be the case. Therefore, the most frequent cipher text letter in positions 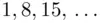 will have come from the enciphering of the letter “e”. Thus, by computing the number of occurrences of each cipher text letter at intervals of 7 letters, we can determine the most frequently occurring cipher text letter and assign it to the plain text letter “e”. Hence, we will have determined the first letter of the keyword. Similar remarks apply to positions {
will have come from the enciphering of the letter “e”. Thus, by computing the number of occurrences of each cipher text letter at intervals of 7 letters, we can determine the most frequently occurring cipher text letter and assign it to the plain text letter “e”. Hence, we will have determined the first letter of the keyword. Similar remarks apply to positions { 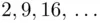 }, {
}, { 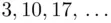 }. In general, if we know the period
}. In general, if we know the period 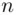 , we can capture the key using frequency analysis.
, we can capture the key using frequency analysis.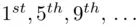 } letters, {
} letters, { 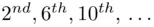 } letters, and so on. Taking the
} letters, and so on. Taking the 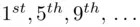 letters, we get
letters, we get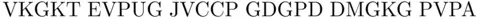
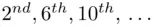 letters), we obtain the following table:
letters), we obtain the following table: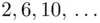 ) besides “e” are “c” and “p.” Finally, a key letter of “O” means that the most frequently occurring letters besides “e” are “t” and “r.”. From the results shown in Table 2.1, it seems that “O” is then the more likely key‐letter. Therefore, we conclude that the second key letter is “O.”
) besides “e” are “c” and “p.” Finally, a key letter of “O” means that the most frequently occurring letters besides “e” are “t” and “r.”. From the results shown in Table 2.1, it seems that “O” is then the more likely key‐letter. Therefore, we conclude that the second key letter is “O.”










