2.2.3.3.2 Nachher-Messung mit Kontrollgruppe
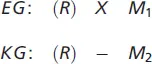
Dieses Design ist anwendbar, wenn die Randomisierungsbedingung in der Weise erfüllt ist, dass vor Beginn des Experiments EG und KG den gleichen Messwert beim abhängigen Merkmal aufweisen. Da dann die Vergleichbarkeit der Gruppen gewährleistet ist, ergibt sich die Experimentwirkung als Differenz zwischen und Das Design hat demnach mehrere Vorteile: Der Verzicht auf die Vorher-Messung verringert die Kosten und vermeidet den Testeffekt. Allerdings gilt dies nur, wenn die Gruppen aufgrund der Randomisierung wirklich völlig vergleichbar sind. Handelt es sich um ausreichend große Stichproben und um eine sorgfältige Zufallsauswahl, so kann davon ausgegangen werden. Andernfalls ist eher eine Vorher-Messung anzuraten.
2.2.3.3.3 Solomon-Vier-Gruppen-Design
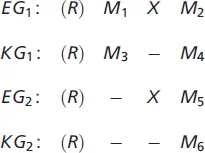
Diese Versuchsanordnung entsteht durch Kombination der beiden vorher genannten Versuchspläne. Durch sie kann der Testeffekt ausgeschaltet werden, da die dritte und vierte Gruppe nicht einer Vorher-Messung unterzogen werden. Zugleich bietet die Vorher-Messung bei den Gruppen 1 und 2 die Möglichkeit, das Ausmaß eines etwaigen Testeffektes zu ermitteln.
Bei diesem Experimentdesign stellt sich nun die Frage, wie die Experimentwirkung gemessen werden soll. Der einfachste Weg besteht darin, dass man annimmt, dass sowohl die zweite Experiment- als auch die zweite Kontrollgruppe im Durchschnitt die gleichen Werte aufweisen wie die jeweiligen Gruppen mit Vormessung. Daher wird als fiktive Vormessung für EG 1und KG 2der Mittelwert aus M 1und M 3herangezogen, d. h (M 1+ M 3)/2. Damit folgt:
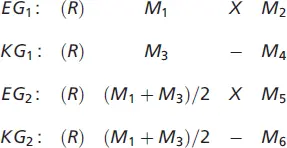
Die Experimentwirkung wird dann analog zur Vorher-Nachher-Messung mit einer Kontrollgruppe berechnet, d. h.
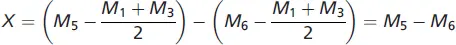
Da EG 1und EG 2keiner Vorher-Messung unterzogen wurden, entfällt der Testeffekt. Genau dieser Effekt kann im Solomon-Vier-Gruppendesign ebenfalls gemessen werden, indem einfach die beiden Experimentgruppen verglichen werden. Ein möglicher Testeffekt kann sich nur in EG 1, nicht jedoch in EG 2niedergeschlagen haben. Der Testeffekt ergibt sich wie folgt:
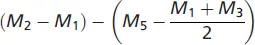
Obwohl das Solomon-Vier-Gruppendesign dem Ideal eines kontrollierten Experiments recht nahekommt, verbietet sein hoher Aufwand zumeist die Anwendung in der Marktforschung.
2.2.3.3.4 Randomisiertes faktorielles Design
Die bisher skizzierten Versuchsanordnungen gingen von einem Experimentfaktor aus, der in zwei Ausprägungen (Stufen) vorlag (z. B. alte und neue Packungsvariante). Eine erste Erweiterung lässt sich dadurch erzielen, dass mehr als zwei Stufen eines Experimentfaktors gleichzeitig überprüft werden. Das »einfaktorielle Design« hat dann z. B. bei drei Stufen folgendes Aussehen:
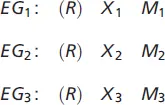
Da hier eventuelle Störfaktoren auf alle Gruppen wirken, benötigt man keine zusätzliche Kontrollgruppe, denn die Differenzbildung lässt auch hier diese Einflüsse wegfallen!
Für viele Fragestellungen in der experimentellen Marktforschung ist auch diese Vorgehensweise noch zu restriktiv. So kann beispielsweise die Frage auftreten, welcher von mehreren Werbeslogans unter gleichzeitiger Berücksichtigung von mehreren Packungsalternativen am besten ist. Es interessiert hierbei die Werbeslogan-Packungs-Kombination, die insgesamt gegenüber anderen Kombinationen am besten abschneidet. Bei zwei- und mehrfaktoriellen Designs werden somit zwei oder mehr Experimentierfaktoren zugleich variiert, wobei jeder Experimentierfaktor in mehreren Ausprägungen vorliegen kann.
Ein einfaches Beispiel soll den Aufbau eines zweifaktoriellen Designs verdeutlichen, wobei von zwei verschiedenen Packungen X 1und X 2sowie zwei verschiedenen Werbeslogans Y 1und Y 2ausgegangen wird. Man spricht daher auch von einem 2 × 2-faktoriellen Design (  Abb. 9).
Abb. 9).
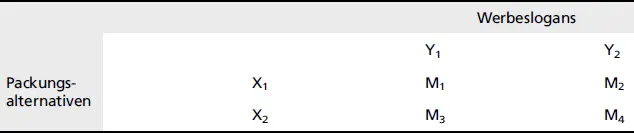
Abb. 9: Aufbau eines zweifaktoriellen Designs
Hierbei handelt es sich um vier Gruppen, die jeweils durch die Stimuluskombinationen X 1Y 1, X 1Y 2, X 2Y 1und X 2Y 2präsentiert werden. Da auch hier die Störgrößen bei allen vier Gruppen zugleich auftreten, erübrigt sich eine Kontrollgruppe. Voraussetzung ist aber, dass die Gruppen nach dem Zufallsprinzip gebildet wurden. Ein Vorteil des zweifaktoriellen Designs liegt darin, dass Interaktionseffekte erfasst werden können: Angenommen, ein faktorielles Experiment zur Überprüfung zweier Packungsalternativen und zweier Werbeslogans habe folgende Kaufabsichtsnennungen (in %) erbracht (  Abb. 10).
Abb. 10).

Abb. 10: Zahlenbeispiel für ein zweifaktorielles Design
Die Wirkungsdifferenz der Packungsalternativen kann aus jeder der beiden Spaltendifferenzen ersehen werden, nämlich 52% − 50% = 2% oder 47% − 45% = 2%. Ebenso verhält es sich mit der Wirkungsdifferenz der Werbeslogans, denn die Zeilendifferenzen 50% − 45% = 5% oder 52% − 47% = 5% sind gleich. Als beste Kombination erweist sich X 2Y 1, mit 52 %. Man bezeichnet diese Differenzen von 2 % bzw. 5 % als Haupteffekte.
Anders im folgenden Beispiel (  Abb. 11).
Abb. 11).
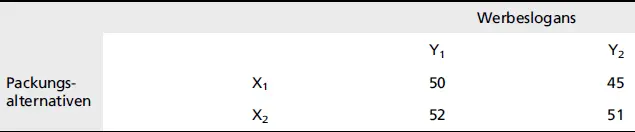
Abb. 11: Alternatives Zahlenbeispiel für ein zweifaktorielles Design
Slogan 1 führt mit Packung 1 zu einer um 5 % höheren Wirkung als Slogan 2; mit Packung 2 beträgt der Unterschied zwischen Slogan 1 und 2 jedoch nur noch 1 %. Umgekehrt hängt die Reaktion auf die Packungen vom jeweiligen Slogan ab: Mit Slogan l ist die Experimentwirkung der Packung 2 um 2 % höher als die der Packung 1; mit Slogan 2 beträgt die entsprechende Differenz der Packungen jedoch 6 %. Zwischen den Packungsalternativen und den verschiedenen Werbeslogans bestehen somit Interaktions- oder Wechselwirkungseffekte, d. h. die Wirkung einer Packung ist abhängig vom jeweiligen Slogan und umgekehrt. Eine isolierte Betrachtung nur der Packungen oder nur der Slogans in zwei Experimenten würde daher nicht ohne weiteres den Schluss zulassen, welche Kombination wirklich die beste ist.
Читать дальше

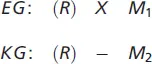
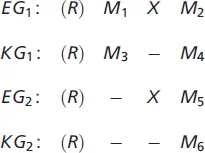
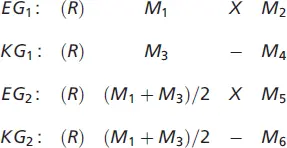
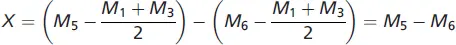
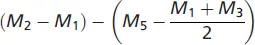
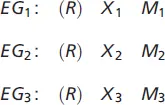
 Abb. 9).
Abb. 9).












