Heymo Böhler - Marktforschung

Die größte Schwäche des Designs besteht in der mangelhaften Kontrolle von Störungen, die im Zeitablauf eintreten können (gesamtwirtschaftliche Einflüsse,

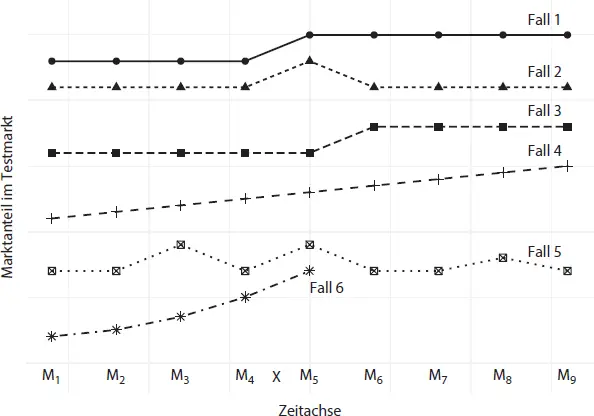
Abb. 12: Panelergebnisse in sechs Fällen im Rahmen eines Zeitreihendesigns

Konkurrenzmaßnahmen usw.). Allerdings kann der Experimentator die Situation auf dem Testmarkt verfolgen und eventuell auftretende Störungen registrieren. Es ist jedoch recht schwierig, ihren Einfluss auf das Experimentergebnis zu quantifizieren.

Die wiederholte Datenerhebung im Rahmen von Panels veranlasste einige Fachvertreter, das Panel als eigenständige Experimentanordnung zu betrachten. Dieser Auffassung wird hier nicht gefolgt. Zwar handelt es sich beim Panel ebenfalls um ein Forschungsdesign (vgl. Mayntz et al. 1978, S. 148), doch erfüllt die wiederholte Messung von Tatbeständen nicht per se die Anforderungen an ein (Quasi-)Experiment. Vielmehr muss der Experimentator, der ein Experiment beabsichtigt, in dessen Rahmen er sich des Panels bedienen möchte, erst selbst durch ein entsprechendes Experimentdesign sicherstellen, dass er zu möglichst unverzerrten Schätzwerten der Experimentwirkung gelangt. Dies wäre z. B. ganz sicher nicht der Fall, wenn er im vorherigen Beispiel nur die Panelmesswerte

EG: M 4X M 5

verwenden würde. Es käme dann in den Fällen 2, 3, 4, 5 und 6 zu völlig falschen Schlussfolgerungen hinsichtlich der Experimentwirkung. Panelmesswerte können allerdings in quasi-experimentellen Designs Verwendung finden, nämlich in Zeitreihendesigns mit und ohne Kontrollgruppe. Bei Heranziehung einer Kontrollgruppe ist wegen der fehlenden Randomisierung außerdem auf eine weitgehende Übereinstimmung der Gruppen in wichtigen Merkmalen zu achten (Betriebsformen des Handels, Größe der Handelsbetriebe etc.). Alles in allem hängt es somit von den Kontrollvorkehrungen des Experimentators ab, inwieweit die Forschungsanordnung des Panels auf »experimentelles Niveau« gehoben wird. So entspricht z. B. der Minimarkttest GfK- BehaviorScan diesen Anforderungen.

In der Mehrzahl der Fälle werden Panels jedoch nur für deskriptive Forschungszwecke genutzt, sei es zur Beschreibung des Marktes, für deskriptive Analysen von Zusammenhängen oder für deskriptive Prognosen, zumal im entsprechenden Zeitabschnitt überhaupt keine »Experimentfaktoren« variiert wurden.

Abschließend werden aus der Vielzahl weiterer quasiexperimenteller Designs, die die Praxis für ihre Bedürfnisse entwickelt hat, lediglich einige skizziert (zur Einführung vgl. Zimmermann 1972, S. 158 ff., Cook und Campbell 1979, S. 210 ff.).

Das Block- Design ist ein quasi-experimentelles Design, das rein äußerlich dem zweifaktoriellen Design gleicht. Allerdings wird neben dem Experimentierfaktor als zweiter Faktor ein externes Kriterium herangezogen, um die Experimenteinheiten in homogene Gruppen (»Blöcke«) einzuteilen. Möchte man z. B. die Wirkung von drei Preisalternativen überprüfen, so bietet es sich an, Einzelhandelsgeschäfte nach dem Umsatz in verschiedene Klassen einzuteilen, um innerhalb eines jeden der so gebildeten Blöcke die drei Preisalternativen zu testen. Gegenüber der Zufallsanordnung mit Experiment- und Kontrollgruppe bzw. mit mehreren Experimentgruppen bei einfaktoriellem Design hat diese Vorgehensweise den Vorteil, dass die vom »Blockfaktor« ausgehende starke Streuung aus den Experimentergebnissen herausgehalten wird.

Die bisherigen Versuchsanordnungen bei zwei- und mehrfaktoriellen Designs gingen davon aus, dass jeder Faktorstufenkombination jeweils eine Zufallsstichprobe zugewiesen wurde. Dies führt sehr rasch zu einer erheblichen Anzahl von Experimentgruppen. Zudem interessieren nicht alle Kombinationen. Aus diesem Grunde bieten sich unvollständige mehrfaktorielle Designs an, bei denen nur jene Kombinationen untersucht werden, die für den Experimentator von Belang sind. In Frage kommen hierfür hierarchische Versuchspläne. wobei jede Stufe eines Experimentfaktors nur mit ganz bestimmten Stufen eines zweiten Experimentfaktors kombiniert wird (z. B. Packungsalternative A mit den Preishöhen l und 2, Packungsalternative B mit den Preishöhen 3 und 4). Darüber hinaus ist auf Varianten unvollständiger Designs wie das Lateinische Quadrat und das Griechisch-Lateinische Quadrat zu verweisen. Sie ermöglichen die gleichzeitige Überprüfung von drei bzw. vier Experimentfaktoren bei erheblicher Reduktion der Versuchsgruppen gegenüber vollständigen faktoriellen Designs, wenn keine Interaktionseffekte gegeben sind.

Die dargestellten Überlegungen zu den Experimentaldesigns beruhen zunächst auf der vereinfachenden Annahme, dass allein unabhängige, im Experiment manipulierte Variable einen direkten Effekt auf die abhängige Variable ausübt. In der Praxis der Marktforschung ebenso wie in der betriebswirtschaftlichen Forschung müssen jedoch oft weitere Variablen für die Erklärung bzw. Einordnung der kausalen Zusammenhänge berücksichtigt werden, da sie einen zusätzlichen Einfluss ausüben. Man spricht hier allgemein von Drittvariablen (third variables), da sie als dritte Variable zu der unabhängigen und der abhängigen Variable hinzutreten und eine, beide, oder den Zusammenhang zwischen beiden Variablen beeinflussen. Zu unterscheiden sind vier wesentliche Typen von Drittvariablen (MacKinnon et al. 2012, S. 2):

• Kovariate: Eine Drittvariable, die weder mit der unabhängigen Variable korreliert, noch einen direkten Einfluss auf deren Zusammenhang mit der abhängigen Variable hat, sondern bei ihrer Berücksichtigung zusätzliche Aufklärung der Streuung der abhängigen Variable leistet (zum Beispiel das Verfügbare Haushaltseinkommen für den Zusammenhang zwischen einer produktpolitischen Maßnahme und der Zahlungsbereitschaft).

• Konfundierende Variable: Eine konfundierende Variable (kurz »confound«) ist eine Variable, die nicht mit erhoben wurde, die aber den Zusammenhang zwischen abhängiger und unabhängiger Variable stark beeinflusst (Beispiel: In einer Studie zur Displaygestaltung für Sommermode im Modehandel und ihren Einfluss auf den Absatz wird das Wetter nicht berücksichtigt, so dass nicht beachtet wird, dass sich Sommermode bei gutem Wetter unabhängig von der Displaygestaltung besser verkauft).

• Moderator: Als Moderatoren werden Drittvariablen bezeichnet, die die Richtung und/oder die Stärke des Zusammenhangs zwischen der unabhängigen und der abhängigen Variable beeinflusst (zum Beispiel die Information über die Absicht hinter einer ungewöhnlichen Werbetaktik für ihre Wirkung auf die Einstellung zur werbenden Marke).

• Mediator: Eine Drittvariable wird als Mediator bezeichnet, wenn sie kausal durch die unabhängige Variable beeinflusst wird, und dieser Mediator dann einen kausalen Einfluss auf die abhängige Variable ausübt (so wirkt beispielweise eine Werbemaßnahme meist über den Mediator »Einstellung zur Werbung« auf die Einstellung zur Marke).

Drittvariablen müssen sorgfältig kontrolliert (konfundierende Variablen) bzw. in das Experimentaldesign integriert werden, damit die kausalen Beziehungen, die das Experiment prüfen soll, nicht verzerrt werden. Bei der Prüfung auf mögliche konfundierende Variablen können Vortests (auch als Pretests bezeichnet, bei denen es sich um vorab durchgeführte Studien handelt, die nicht mit den Pretests in Pretest-Posttest-Designs verwechselt werden dürfen) durchgeführt oder Messinstrumente in der Hauptstudie eingesetzt werden. Vortests bieten im Gegensatz zur Confound-Kontrolle erst in der Hauptstudie die Chance, die konfundierenden Einflüsse für die Hauptstudie auszuschließen, und zugleich vorab zu prüfen, ob die experimentelle Manipulation stark genug ausgefallen ist (Perdue und Summers 1986; Vargas et al. 2017). Einen hervorragenden vertiefenden Überblick über Fragestellungen zur praktischen Durchführung von Experimenten und der Behandlung von Drittvariablen bietet der Beitrag von Spilski et al. (2018). Zur empirischen Prüfung der Einflüsse von Kovariaten, Moderatoren und Mediatoren in Experimenten wird in jüngere Zeit vielfach das Makro PROCESS für SPSS, SAS und R verwendet ( https://www.processmacro.org/index.html), zu dem auch eine umfassende statistische Einführung existiert (Hayes 2018).