1 ...6 7 8 10 11 12 ...15
1.2.4.2. First top-down pass
In the first top-down pass, the second quad-tree is swept downward from the root to the leaves to calculate the prior P(cs) recursively. This prior is initialized in each site 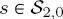 of the root of the second quad-tree as
of the root of the second quad-tree as 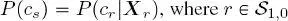 is the site of the root of the first quad-tree with the same spatial location as s . The partial posterior marginal
is the site of the root of the first quad-tree with the same spatial location as s . The partial posterior marginal 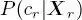 has been derived in the aforementioned initialization. Then, the top-down pass travels along the other layers until it reaches the leaves
has been derived in the aforementioned initialization. Then, the top-down pass travels along the other layers until it reaches the leaves 
[1.7] 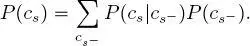
This formulation encourages parent and children sites to share the same class label, although it does not deterministically enforce this condition. It also implies a model for the statistical relations between labels in consecutive layers. Here, the parent–child transition probability 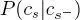 is expressed using the parametric model in Bouman (1991):
is expressed using the parametric model in Bouman (1991):
[1.8] 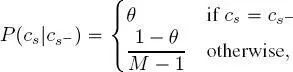
where 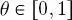 is a hyperparameter of the method. Experiments conducted in Hedhli et al. (2016) indicated limited sensitivity of the result of MPM on multiple cascaded quad-trees to the value of this hyperparameter. We also note that equation [1.8]implicitly yields a stationary model for the considered transitions, i.e. the probability
is a hyperparameter of the method. Experiments conducted in Hedhli et al. (2016) indicated limited sensitivity of the result of MPM on multiple cascaded quad-trees to the value of this hyperparameter. We also note that equation [1.8]implicitly yields a stationary model for the considered transitions, i.e. the probability 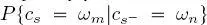 depends on the pair
depends on the pair 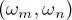 of classes, but not on the specific site location
of classes, but not on the specific site location 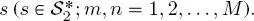
After the first top-down pass, the prior P ( cs ) is known on every site s of the second quad-tree.
To calculate 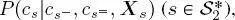 a bottom-up step traveling through the second quad-tree from the leaves to the root is used. It is based on equation [1.6], in which, besides the priors P(cs) , which are known from the first top-down pass, three further probability distributions are necessary: (i) the transition probabilities at the same scale
a bottom-up step traveling through the second quad-tree from the leaves to the root is used. It is based on equation [1.6], in which, besides the priors P(cs) , which are known from the first top-down pass, three further probability distributions are necessary: (i) the transition probabilities at the same scale 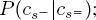 (ii) the parent–child transition probabilities
(ii) the parent–child transition probabilities 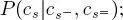 and (iii) the partial posterior marginals
and (iii) the partial posterior marginals 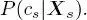
Concerning (i), the algorithm in Bruzzone et al. (1999) is applied to estimate the multitemporal joint probability matrix, i.e. the M × M matrix J , whose ( m, n )-th entry is 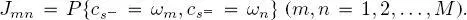 This technique is based on the expectation maximization (EM) algorithm and addresses the problem of learning these joint probabilities as a parametric estimation task. More details can be found in Hedhli et al. (2016). Once J has been estimated,
This technique is based on the expectation maximization (EM) algorithm and addresses the problem of learning these joint probabilities as a parametric estimation task. More details can be found in Hedhli et al. (2016). Once J has been estimated, 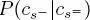 is derived as an obvious byproduct.
is derived as an obvious byproduct.
With regard to (ii), the parametric model in equation [1.8]is extended as follows:
[1.9] 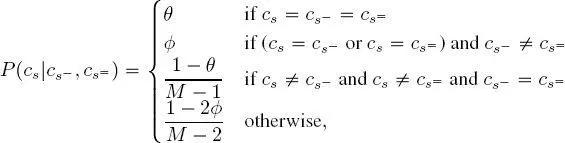
where θ has the same meaning as in equation [1.8]and 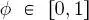 is a second hyperparameter.
is a second hyperparameter.
Concerning (iii), it has been proved that, on all layers except the leaves (Laferté et al. 2000):
[1.10] 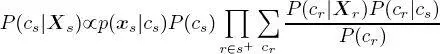
for all sites 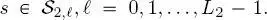 First,
First, 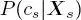 is initialized on the leaves of the second quad-tree by setting
is initialized on the leaves of the second quad-tree by setting 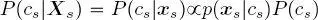 for
for 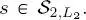 Then,
Then, 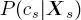 is calculated by using equation [1.10]while sweeping the second quad-tree upward until the root is reached. This recursive process makes use of the pixelwise class-conditional PDF
is calculated by using equation [1.10]while sweeping the second quad-tree upward until the root is reached. This recursive process makes use of the pixelwise class-conditional PDF 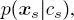 whose modeling is discussed in section 1.2.5. After the bottom-up pass,
whose modeling is discussed in section 1.2.5. After the bottom-up pass, 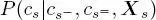 is known on every site s of the second quad-tree.
is known on every site s of the second quad-tree.
Читать дальше

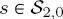 of the root of the second quad-tree as
of the root of the second quad-tree as 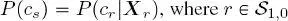 is the site of the root of the first quad-tree with the same spatial location as s . The partial posterior marginal
is the site of the root of the first quad-tree with the same spatial location as s . The partial posterior marginal 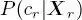 has been derived in the aforementioned initialization. Then, the top-down pass travels along the other layers until it reaches the leaves
has been derived in the aforementioned initialization. Then, the top-down pass travels along the other layers until it reaches the leaves 
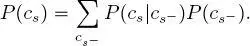
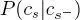 is expressed using the parametric model in Bouman (1991):
is expressed using the parametric model in Bouman (1991):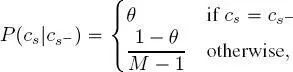
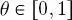 is a hyperparameter of the method. Experiments conducted in Hedhli et al. (2016) indicated limited sensitivity of the result of MPM on multiple cascaded quad-trees to the value of this hyperparameter. We also note that equation [1.8]implicitly yields a stationary model for the considered transitions, i.e. the probability
is a hyperparameter of the method. Experiments conducted in Hedhli et al. (2016) indicated limited sensitivity of the result of MPM on multiple cascaded quad-trees to the value of this hyperparameter. We also note that equation [1.8]implicitly yields a stationary model for the considered transitions, i.e. the probability 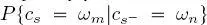 depends on the pair
depends on the pair 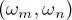 of classes, but not on the specific site location
of classes, but not on the specific site location 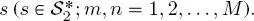
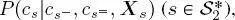 a bottom-up step traveling through the second quad-tree from the leaves to the root is used. It is based on equation [1.6], in which, besides the priors P(cs) , which are known from the first top-down pass, three further probability distributions are necessary: (i) the transition probabilities at the same scale
a bottom-up step traveling through the second quad-tree from the leaves to the root is used. It is based on equation [1.6], in which, besides the priors P(cs) , which are known from the first top-down pass, three further probability distributions are necessary: (i) the transition probabilities at the same scale 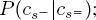 (ii) the parent–child transition probabilities
(ii) the parent–child transition probabilities 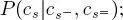 and (iii) the partial posterior marginals
and (iii) the partial posterior marginals 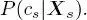
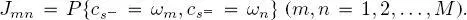 This technique is based on the expectation maximization (EM) algorithm and addresses the problem of learning these joint probabilities as a parametric estimation task. More details can be found in Hedhli et al. (2016). Once J has been estimated,
This technique is based on the expectation maximization (EM) algorithm and addresses the problem of learning these joint probabilities as a parametric estimation task. More details can be found in Hedhli et al. (2016). Once J has been estimated, 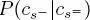 is derived as an obvious byproduct.
is derived as an obvious byproduct.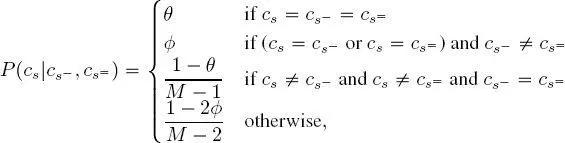
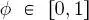 is a second hyperparameter.
is a second hyperparameter.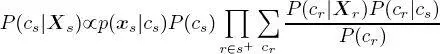
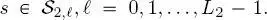 First,
First, 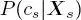 is initialized on the leaves of the second quad-tree by setting
is initialized on the leaves of the second quad-tree by setting 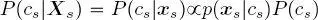 for
for 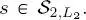 Then,
Then, 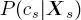 is calculated by using equation [1.10]while sweeping the second quad-tree upward until the root is reached. This recursive process makes use of the pixelwise class-conditional PDF
is calculated by using equation [1.10]while sweeping the second quad-tree upward until the root is reached. This recursive process makes use of the pixelwise class-conditional PDF 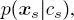 whose modeling is discussed in section 1.2.5. After the bottom-up pass,
whose modeling is discussed in section 1.2.5. After the bottom-up pass, 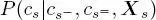 is known on every site s of the second quad-tree.
is known on every site s of the second quad-tree.










