In this framework, two specific algorithms are defined. In the first one, the k -th image in the series is assigned to a separate quad-tree based on its own spatial resolution. A hierarchical MRF is defined on this quad-tree topology, and inference on the resulting probabilistic graphical model is addressed using the Bayesian marginal posterior mode (MPM) criterion (Kato and Zerubia 2012). In the second proposed algorithm, the focus is on a specific case of multimission, multifrequency and multiresolution time series: multifrequency X-band COSMO-SkyMed and C-band RADARSAT-2 SAR images are used alongside optical visible and near-infrared (VNIR) Pléiades data. This scenario is of special current interest, both because of the potential of exploiting the synergy among these missions and especially in view of the recent COSMO-SkyMed Second Generation and RADARSAT Constellation programs. In the case of the second method, different quad-trees are also used, but both optical and SAR data are associated with each quad-tree in order to benefit from the finest resolution available from the considered sensors. Both approaches exploit the potential of hierarchical probabilistic graphical models (Kato and Zerubia 2012) to address challenging problems of multimodal classification of an image time series.
1.2.2. Hierarchical model associated with the first proposed method
Let us first define the multiple quad-tree structure associated with the first proposed method. The K images 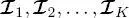 in the series are included in the finest-scale layers (i.e. the leaves) of K distinct quad-trees. The coarser-scale layers of each quad-tree are filled in by applying wavelet transforms to the image on the finest-scale layer (Mallat 2008). The roots of the K quad-trees are assumed to correspond to the same spatial resolution. The rationale of this hierarchical structure is that each image in the input series originates from a separate multiscale quad-tree, generally with a different number of layers and the input image on the leaves, and that the roots of these quad-trees share a common spatial resolution (see Figure 1.4). This graph topology implicitly means that the spatial resolutions of the input images in the series are in a power-of-2 mutual relation. In general terms, this is a restriction but when concerning current high-resolution satellite missions, this condition is easily met up to possible minor resampling.
in the series are included in the finest-scale layers (i.e. the leaves) of K distinct quad-trees. The coarser-scale layers of each quad-tree are filled in by applying wavelet transforms to the image on the finest-scale layer (Mallat 2008). The roots of the K quad-trees are assumed to correspond to the same spatial resolution. The rationale of this hierarchical structure is that each image in the input series originates from a separate multiscale quad-tree, generally with a different number of layers and the input image on the leaves, and that the roots of these quad-trees share a common spatial resolution (see Figure 1.4). This graph topology implicitly means that the spatial resolutions of the input images in the series are in a power-of-2 mutual relation. In general terms, this is a restriction but when concerning current high-resolution satellite missions, this condition is easily met up to possible minor resampling.
Let 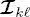 be the image associated with the
be the image associated with the 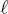 -th layer of the k -th quad-tree in the series. We will index the common root with
-th layer of the k -th quad-tree in the series. We will index the common root with 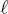 = 0 and the leaves of the k -th quad-tree with
= 0 and the leaves of the k -th quad-tree with 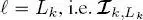 coincides with the original input image
coincides with the original input image 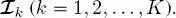 The images
The images 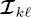 in the other layers
in the other layers  have been obtained through wavelets from
have been obtained through wavelets from 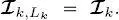 The whole time series of multiscale images, either acquired by the considered sensors or obtained through wavelets, will be denoted as
The whole time series of multiscale images, either acquired by the considered sensors or obtained through wavelets, will be denoted as 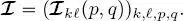 .
.
We will also indicate as 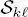 the pixel lattice of the
the pixel lattice of the 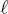 -th layer of the k -th quadtree
-th layer of the k -th quadtree 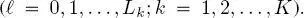 . We will denote as s = (p, q) the coordinate pair of a generic pixel in one of these layers
. We will denote as s = (p, q) the coordinate pair of a generic pixel in one of these layers 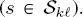 . Following the literature of hierarchical MRFs, the site will be named s in the following. Sites in the described quad-tree structure are linked by parent–child relations – within each quad-tree and across consecutive quad-trees – as a function of their spatial scale. Specifically, if
. Following the literature of hierarchical MRFs, the site will be named s in the following. Sites in the described quad-tree structure are linked by parent–child relations – within each quad-tree and across consecutive quad-trees – as a function of their spatial scale. Specifically, if 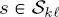 is a site in the
is a site in the 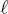 -th layer of the k -th quadtree and
-th layer of the k -th quadtree and 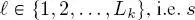 is not on the root layer, then
is not on the root layer, then 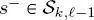 indicates its parent node in the same quad-tree ( k = 1, 2,..., K ). Similarly, if
indicates its parent node in the same quad-tree ( k = 1, 2,..., K ). Similarly, if 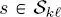 with
with  i.e. s is not on the leaves layer, then
i.e. s is not on the leaves layer, then 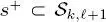 denotes the set of its four children nodes in the same quad-tree. Finally, if
denotes the set of its four children nodes in the same quad-tree. Finally, if 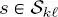 with
with  and
and 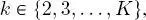 i.e. if s is neither in the first quad-tree of the series nor in the root of the other quad-trees, then
i.e. if s is neither in the first quad-tree of the series nor in the root of the other quad-trees, then 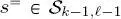 indicates its parent node in the ( k – 1)-th quad-tree, i.e. in the quad-tree associated with the previous image of the series (see Figure 1.4). From a graph-theoretic perspective, if the sites in the quad-trees are meant as nodes in a graph, then the pairs ( s, s– ), ( s, s= ) and ( s, r ) with
indicates its parent node in the ( k – 1)-th quad-tree, i.e. in the quad-tree associated with the previous image of the series (see Figure 1.4). From a graph-theoretic perspective, if the sites in the quad-trees are meant as nodes in a graph, then the pairs ( s, s– ), ( s, s= ) and ( s, r ) with 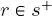 define the corresponding edges.
define the corresponding edges.
Читать дальше

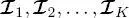 in the series are included in the finest-scale layers (i.e. the leaves) of K distinct quad-trees. The coarser-scale layers of each quad-tree are filled in by applying wavelet transforms to the image on the finest-scale layer (Mallat 2008). The roots of the K quad-trees are assumed to correspond to the same spatial resolution. The rationale of this hierarchical structure is that each image in the input series originates from a separate multiscale quad-tree, generally with a different number of layers and the input image on the leaves, and that the roots of these quad-trees share a common spatial resolution (see Figure 1.4). This graph topology implicitly means that the spatial resolutions of the input images in the series are in a power-of-2 mutual relation. In general terms, this is a restriction but when concerning current high-resolution satellite missions, this condition is easily met up to possible minor resampling.
in the series are included in the finest-scale layers (i.e. the leaves) of K distinct quad-trees. The coarser-scale layers of each quad-tree are filled in by applying wavelet transforms to the image on the finest-scale layer (Mallat 2008). The roots of the K quad-trees are assumed to correspond to the same spatial resolution. The rationale of this hierarchical structure is that each image in the input series originates from a separate multiscale quad-tree, generally with a different number of layers and the input image on the leaves, and that the roots of these quad-trees share a common spatial resolution (see Figure 1.4). This graph topology implicitly means that the spatial resolutions of the input images in the series are in a power-of-2 mutual relation. In general terms, this is a restriction but when concerning current high-resolution satellite missions, this condition is easily met up to possible minor resampling.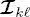 be the image associated with the
be the image associated with the 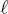 -th layer of the k -th quad-tree in the series. We will index the common root with
-th layer of the k -th quad-tree in the series. We will index the common root with 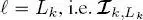 coincides with the original input image
coincides with the original input image 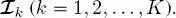 The images
The images 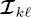 in the other layers
in the other layers  have been obtained through wavelets from
have been obtained through wavelets from 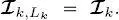 The whole time series of multiscale images, either acquired by the considered sensors or obtained through wavelets, will be denoted as
The whole time series of multiscale images, either acquired by the considered sensors or obtained through wavelets, will be denoted as 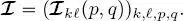 .
.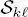 the pixel lattice of the
the pixel lattice of the 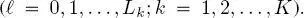 . We will denote as s = (p, q) the coordinate pair of a generic pixel in one of these layers
. We will denote as s = (p, q) the coordinate pair of a generic pixel in one of these layers 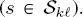 . Following the literature of hierarchical MRFs, the site will be named s in the following. Sites in the described quad-tree structure are linked by parent–child relations – within each quad-tree and across consecutive quad-trees – as a function of their spatial scale. Specifically, if
. Following the literature of hierarchical MRFs, the site will be named s in the following. Sites in the described quad-tree structure are linked by parent–child relations – within each quad-tree and across consecutive quad-trees – as a function of their spatial scale. Specifically, if 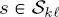 is a site in the
is a site in the 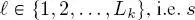 is not on the root layer, then
is not on the root layer, then 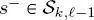 indicates its parent node in the same quad-tree ( k = 1, 2,..., K ). Similarly, if
indicates its parent node in the same quad-tree ( k = 1, 2,..., K ). Similarly, if 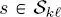 with
with  i.e. s is not on the leaves layer, then
i.e. s is not on the leaves layer, then 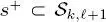 denotes the set of its four children nodes in the same quad-tree. Finally, if
denotes the set of its four children nodes in the same quad-tree. Finally, if 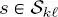 with
with  and
and 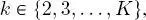 i.e. if s is neither in the first quad-tree of the series nor in the root of the other quad-trees, then
i.e. if s is neither in the first quad-tree of the series nor in the root of the other quad-trees, then 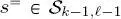 indicates its parent node in the ( k – 1)-th quad-tree, i.e. in the quad-tree associated with the previous image of the series (see Figure 1.4). From a graph-theoretic perspective, if the sites in the quad-trees are meant as nodes in a graph, then the pairs ( s, s– ), ( s, s= ) and ( s, r ) with
indicates its parent node in the ( k – 1)-th quad-tree, i.e. in the quad-tree associated with the previous image of the series (see Figure 1.4). From a graph-theoretic perspective, if the sites in the quad-trees are meant as nodes in a graph, then the pairs ( s, s– ), ( s, s= ) and ( s, r ) with 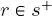 define the corresponding edges.
define the corresponding edges.










