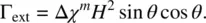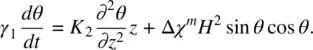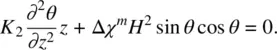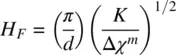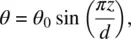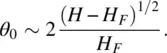(3.66) 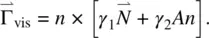
Here 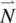 is the rate of change of the director with respect to the immobile background fluid, given by
is the rate of change of the director with respect to the immobile background fluid, given by
(3.67) 
where  is the angular velocity of the liquid. In Eq. (3.66)
is the angular velocity of the liquid. In Eq. (3.66)  is the velocity gradient tensor defined by Eq. (3.60).
is the velocity gradient tensor defined by Eq. (3.60).
The viscosity coefficients γ 1and γ 2are related to the Leslie coefficient α s by [3]
(3.68a) 
(3.68b) 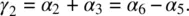
Consider the flow configuration depicted in Figure 3.11. Without the magnetic field and setting ϕ = 0, we have
(3.69a) 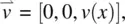
(3.69b) 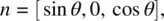
(3.69c) 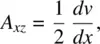
(3.69d) 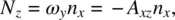
(3.69e) 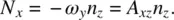
From Eq. (3.66)the viscous torque along the y ‐direction is given by
(3.70) 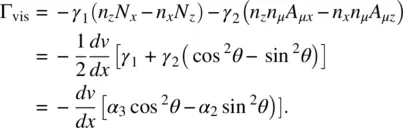
In the steady state, from which the shear torque vanishes, a stable director axis orientation is induced by the flow with an angle θ flowgiven by
(3.71) 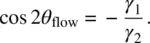
For more complicated flow geometries, the director axis orientation will assume correspondingly complex profiles.
3.6. FIELD‐INDUCED DIRECTOR AXIS REORIENTATION EFFECTS
We now consider the process of director axis reorientation by an external static or low‐frequency field. Optical field effects are discussed in Chapter 6. The following examples will illustrate some of the important relationships among the various torques and dynamical effects discussed in the preceding sections. We will consider the magnetic field as it does not involve complicated local field effects and other electric phenomena (e.g. conduction). The electric field counterparts of the results obtained here for the magnetic field can be simply obtained by the replacement of Δ χ m H 2by Δ εE 2(cf. Eqs. [ 3.26] and [ 3.29]).
3.6.1. Field‐induced Reorientation Without Flow Coupling: Freedericksz Transition
The following example demonstrates how the viscosity coefficient γ 1comes into play in field‐induced reorientational effects. Consider pure twist deformation caused by an externally applied field 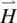 on a planar sample as depicted in Figure 3.12. Let θ denote the angle of deformation. The director axis
on a planar sample as depicted in Figure 3.12. Let θ denote the angle of deformation. The director axis 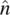 is thus given by
is thus given by 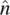 = (cos θ , sin θ , 0). From this and the preceding equations, the free energy ( Eq. 3.4) and elastic torque ( Eq. 3.13) are, respectively,
= (cos θ , sin θ , 0). From this and the preceding equations, the free energy ( Eq. 3.4) and elastic torque ( Eq. 3.13) are, respectively,
(3.72a) 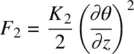
and
(3.72b) 
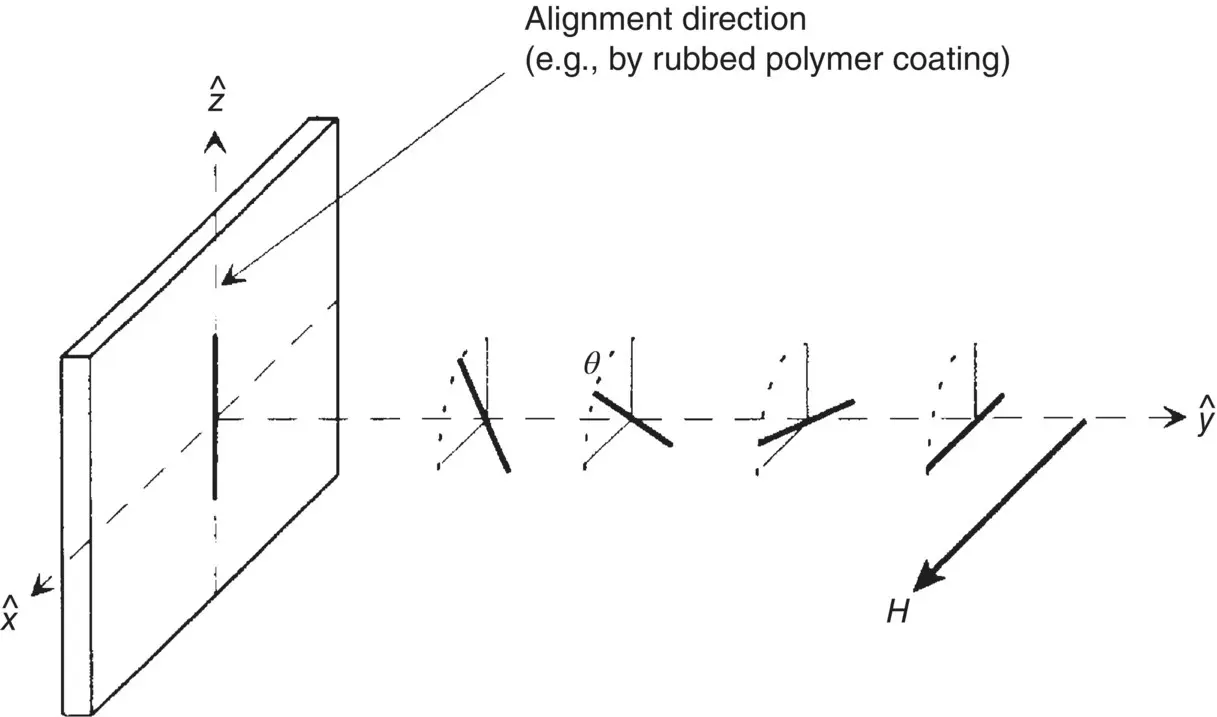
Figure 3.12. Pure twist deformation induced by an external magnetic field H on a planar sample; there is no fluid motion.
The viscous torque is given by
(3.73) 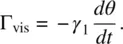
The torque exerted by the external field 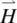 (applied perpendicular to the initial director axis), from Eq. (3.29), becomes
(applied perpendicular to the initial director axis), from Eq. (3.29), becomes
(3.74) 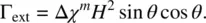
Hence, the torque balance τ equation gives
(3.75a) 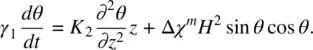
In the equilibrium situation, γ 1 dθ / dt = 0, and Eq. (3.75a)becomes
(3.75b) 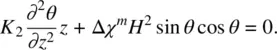
An interesting result from this equation is the so‐called Freedericksz transition [3]. For an applied field strength less than a critical field H F, θ = 0. For H > H F, reorientation occurs. The expression for H Fis given by
(3.76) 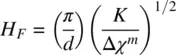
assuming that the reorientation obeys the hard‐boundary (strong anchoring) condition (i.e. θ = 0 at z = 0 and at z = d ). For H just above H F, θ is given approximately by
(3.77a) 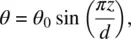
where
(3.77b) 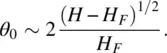
Читать дальше

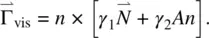
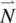 is the rate of change of the director with respect to the immobile background fluid, given by
is the rate of change of the director with respect to the immobile background fluid, given by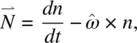
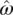 is the angular velocity of the liquid. In Eq. (3.66)
is the angular velocity of the liquid. In Eq. (3.66) 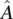 is the velocity gradient tensor defined by Eq. (3.60).
is the velocity gradient tensor defined by Eq. (3.60).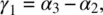
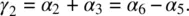
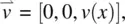
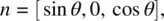
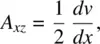
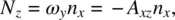
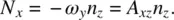
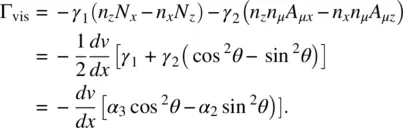
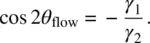
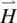 on a planar sample as depicted in Figure 3.12. Let θ denote the angle of deformation. The director axis
on a planar sample as depicted in Figure 3.12. Let θ denote the angle of deformation. The director axis 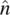 is thus given by
is thus given by 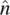 = (cos θ , sin θ , 0). From this and the preceding equations, the free energy ( Eq. 3.4) and elastic torque ( Eq. 3.13) are, respectively,
= (cos θ , sin θ , 0). From this and the preceding equations, the free energy ( Eq. 3.4) and elastic torque ( Eq. 3.13) are, respectively,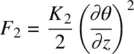


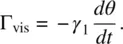
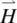 (applied perpendicular to the initial director axis), from Eq. (3.29), becomes
(applied perpendicular to the initial director axis), from Eq. (3.29), becomes