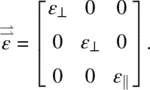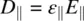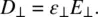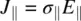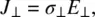On the other hand, if the molecules are not strongly anchored to the boundary, that is, the so‐called soft‐boundary condition ( Figure 3.3), an applied field will perturb the orientation of the molecules at the cell boundaries. In this case, a quantitative description of the dynamics of the field‐induced effects must account for these surface energy terms. A good account of surface energy interaction may be found in the work of Barbero and Simoni [4], which treats the case of optical‐field‐induced effects in a hybrid aligned nematic liquid crystal cell.
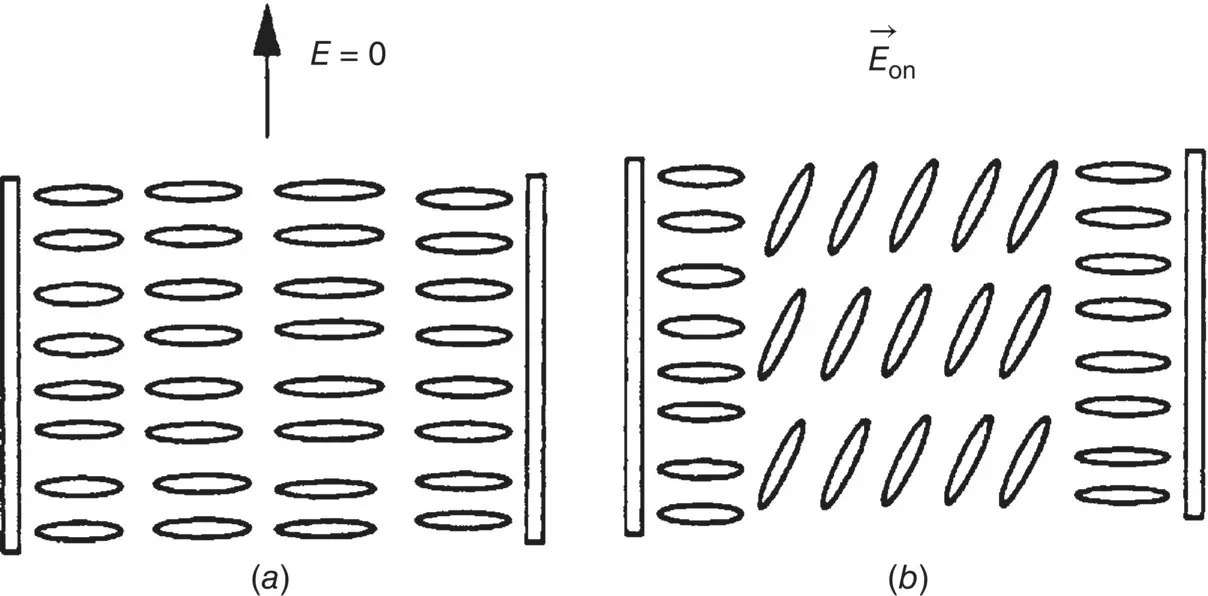
Figure 3.2. A homeotropic nematic liquid crystal with strong surface anchoring: (a) external field off; (b) external field on – only the bulk director axis is deformed.
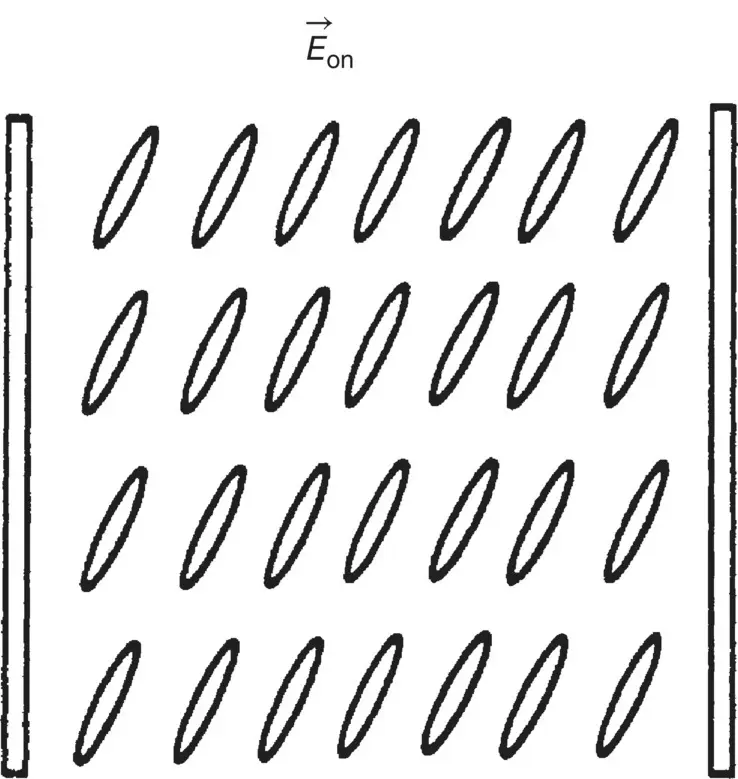
Figure 3.3. Soft‐boundary condition. The applied field will reorient both the surface and bulk director axis.
From Eq. (3.6)for the free energy, one can obtain the corresponding so‐called molecular fields  using the Lagrange equation [3]. In spatial coordinate component form, we have
using the Lagrange equation [3]. In spatial coordinate component form, we have
(3.9) 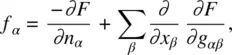
where
(3.10) 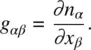
More explicitly, Eq. (3.9)gives, for the total molecular field associated with splay, twist, and bend deformations,
(3.11) 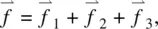
and torque 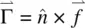 , where
, where
(3.12) 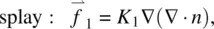
(3.13) 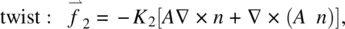
(3.14) 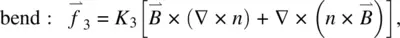
with 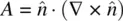 and
and 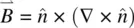 .
.
3.3. DIELECTRIC CONSTANTS AND REFRACTIVE INDICES
Dielectric constants and refractive indices, as well as electrical conductivities of liquid crystals, are physical parameters that characterize the electronic responses of liquid crystals to externally applied fields (electric, magnetic, or optical). Because of the molecular and energy level structures of nematic molecules, these responses are highly dependent on the direction and the frequencies of the field. Accordingly, we shall classify our studies of dielectric permittivity and other electro‐optical parameters into two distinctive frequency regimes: (1) dc and low frequency and (2) optical frequency. Where the transition from the regime (1) to (2) occurs, of course, is governed by the dielectric relaxation processes and the dynamical time constant; typically, the Debye relaxation frequencies in nematics are on the order of 10 10Hz.
3.3.1. DC and Low‐frequency Dielectric Permittivity, Conductivities, and Magnetic Susceptibility
The dielectric constant ε is defined by the Maxwell equation [5]:
(3.15a) 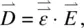
where 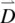 is the displacement current,
is the displacement current, 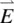 is the electric field, and
is the electric field, and 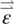 is the tensor. For a uniaxial nematic liquid crystal, we have
is the tensor. For a uniaxial nematic liquid crystal, we have
(3.15b) 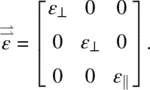
Equations (3.15a)and (3.15b)yield, for the two principal axes,
(3.16) 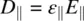
and
(3.17) 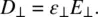
Typical values of ε ||and ε ⊥are on the order of 5 ε 0, where ε 0is the permittivity of free space. Similarly, the electric conductivities σ ||and σ ⊥of nematics are defined by
(3.18) 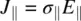
and
(3.19) 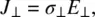
where J ∥and J ⊥are the currents flowing along and perpendicularly to the director axis, respectively. In conjunction with an applied dc electric field, the conductivity anisotropy could give rise to space charge accumulation and create strong director axis reorientation in a nematic film, giving rise to an orientational photorefractive [6] effect (see Chapter 8).
Most nematics (e.g. E7, pentyl cyanobiphenyl [5CB], etc.) are said to possess positive (dielectric) anisotropy ( ε ||> ε ⊥). On the other hand, some nematics, such as MBBA, possess negative anisotropy (i.e. ε ||< ε ⊥). The controlling factors are the molecular constituents and structures.
In general, ε ||and ε ⊥have different dispersion regions, as shown in Figure 3.4for 4‐methoxy‐4′‐ n ‐butylazoxy‐benzene [7], which possess negative dielectric anisotropy (Δ ε < 0). Also plotted in Figure 3.4is the dispersion of ε iso, the dielectric constant for the isotropic case. Notice that for frequencies of 10 9Hz or less, ε ⊥> ε ||. At higher frequencies and in the optical regime, ε ||> ε ⊥(i.e. the dielectric anisotropy changes sign).
For some nematic liquid crystals, this changeover in the sign of Δ ε = ε ||− ε ⊥occurs at a much lower frequency (cf. Figure 3.5for phenylbenzoates [8]). This changeover frequency f cois lower because of the long three‐ringed molecular structure, which is highly resistant to the rotation of molecules around the short axes.
Читать дальше



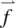 using the Lagrange equation [3]. In spatial coordinate component form, we have
using the Lagrange equation [3]. In spatial coordinate component form, we have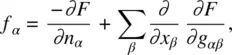
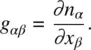
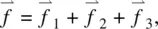
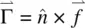 , where
, where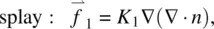
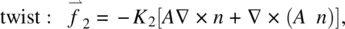
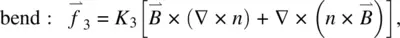
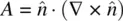 and
and 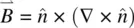 .
.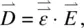
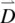 is the displacement current,
is the displacement current, 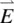 is the electric field, and
is the electric field, and 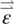 is the tensor. For a uniaxial nematic liquid crystal, we have
is the tensor. For a uniaxial nematic liquid crystal, we have