Iam-Choon Khoo - Liquid Crystals

Unlike the change in order parameter, which is a collective molecular effect, the change in density dρ arises from the individual responses of the molecules and responds relatively quickly to the temperature change.

These results are reflected in Figure 2.3a and b. The diffracted signal contains an initial “spike,” which rises and decays away in the time scale on the order of the laser pulse. As shown in more detail in Chapter 9, this contribution comes from laser‐induced electrostriction or density changes that affect local order. On the other hand, the slowly rising contribution comes from laser‐induced temperature rise Δ T and the resulting order parameter change S (Δ T ). The rate of change depends on the temporal characteristics of the incident laser. The buildup time is about 175 μs with microsecond infrared (10.6 μm) laser pulse (cf. Figure 2.3a) and 30 μs with nanosecond visible (0.53 μm) laser pulse (cf. Figure 2.3b).

Dynamical grating diffraction is thus a useful optical tool to probe the dynamics of the response of order parameter for molecules in various electronic/rovibrational energy states; in particular, the critical “slowing down” of the order parameter near T cas shown in Figure 2.4for the observed order parameter response times as the temperature approaches T cobtained with infrared microseconds laser pulses.

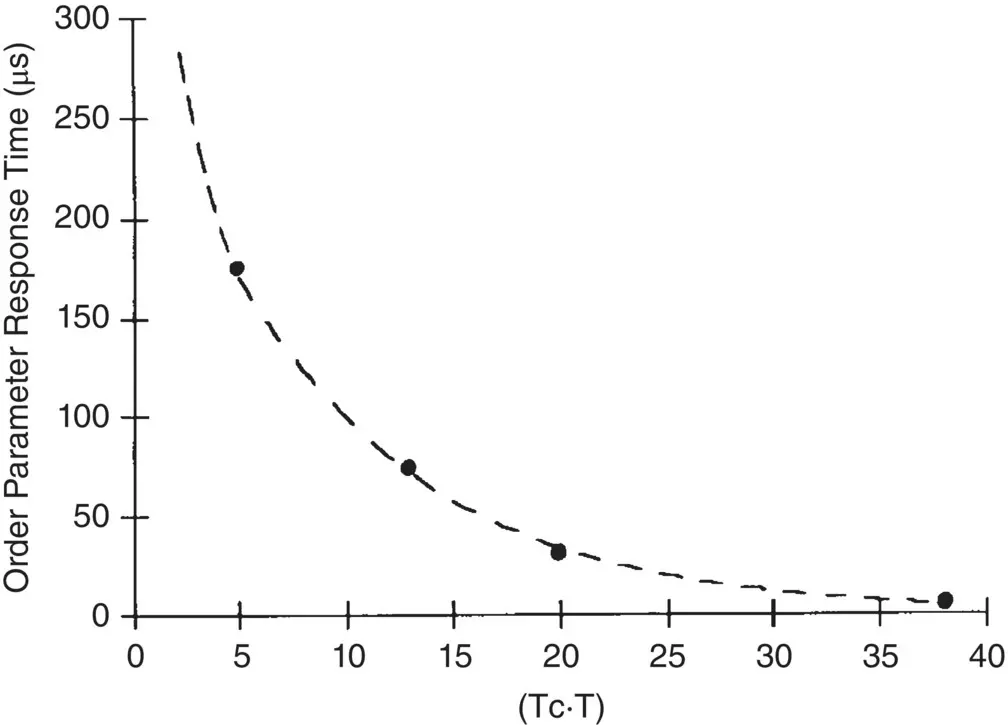
Figure 2.4. Observed buildup times of the diffracted signal associated with order parameter change as a function of the temperature vicinity of T c; excitation by infrared microsecond laser pulses on E7 nematic film.

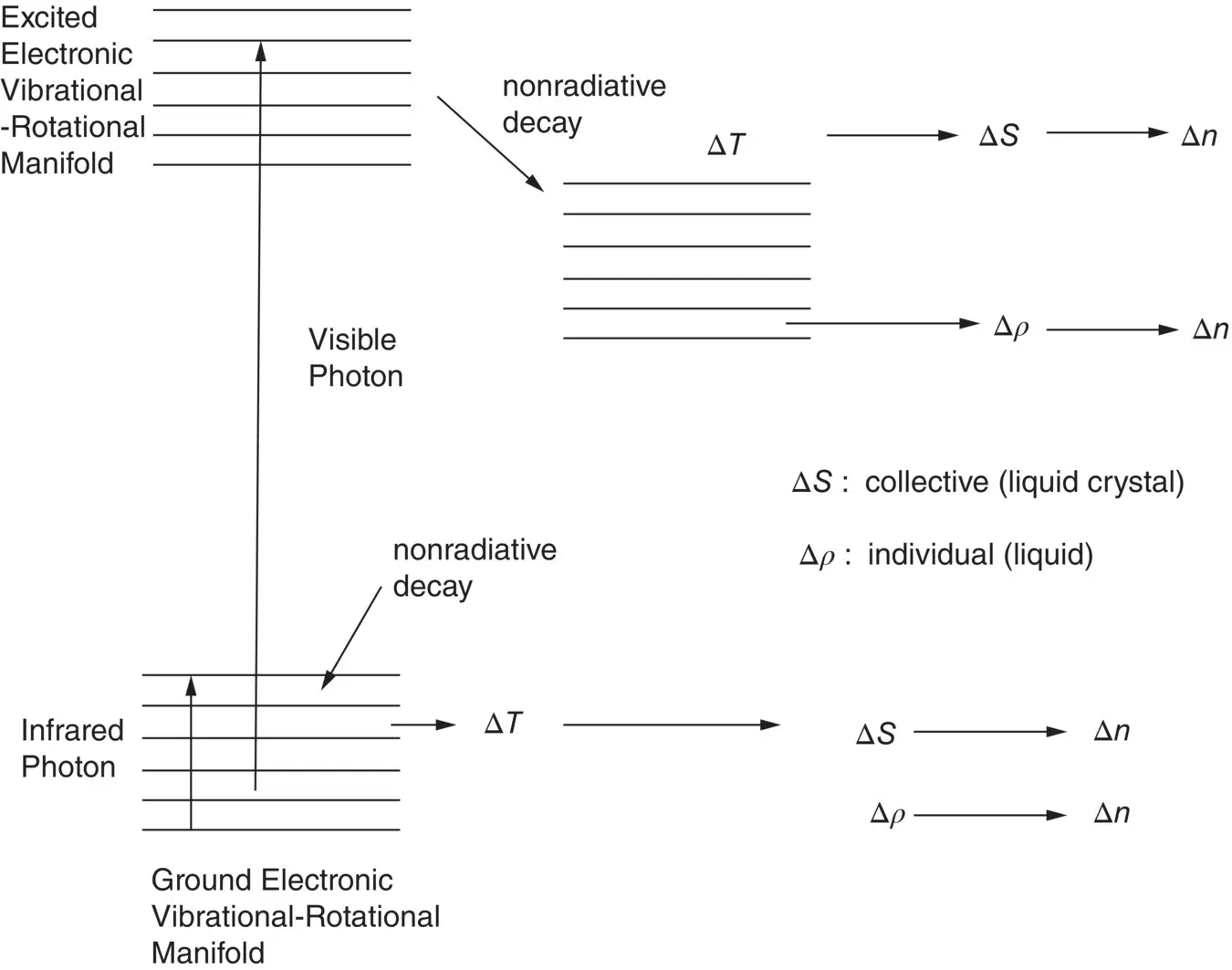
Figure 2.5. Schematic depiction of the molecular levels involved in ground electronic state rovibrational excitations by infrared photo absorptions and excited electronic state excitation by visible photo absorptions.

One can also see from the relative heights of the density and order parameter components in Figure 2.3a and b that the overall response of the nematic film is different for the two forms of excitation. Absorption of infrared photons ( λ = 10.6 μm) corresponds to the excitation of the ground (electronic) state’s rovibrational manifold, whereas the visible photo‐absorption ( λ = 0.53 μm) corresponds to excitation of the molecules to the electronically excited states (cf. Figure 2.5). The electronic molecular structures of these two excited states are different and may therefore account for the different dynamical response behavior of the order parameter, which is dependent on the intermolecular Coulombic dipole–dipole interaction.

More on order parameter dynamics in the context of nonlinear optical responses and switching devices based on laser‐induced order parameter changes in liquid crystals are given in Chapters 9and 12.

Above T c,liquid crystals lose their directional order and behave in many respects like liquids. All bulk physical parameters also assume an isotropic form, although the molecules are anisotropic.

The isotropic phase is, nevertheless, a very interesting and important phase for both fundamental and applied studies. It is fundamentally interesting because of the existence of short‐range order, which gives rise to the critical temperature dependence of various physical parameters just above the phase transition temperature. These critical behaviors provide a good testing ground for liquid crystal physics.

On the other hand, recent studies have also shown that isotropic liquid crystals may be superior in many ways for constructing practical nonlinear optical devices (see Chapter 12), in comparison to the other liquid crystalline phases (see Chapter 8). In general, the scattering loss is less and thus allows longer interaction lengths, and relaxation times are on a much faster scale. These properties easily make up for the smaller optical nonlinearity for practical applications.

We begin our discussion of the isotropic phase of liquid crystals with the free energy of the system, following deGennes’ pioneering theoretical development [1, 2]. The starting point is the order parameter, which we denote by Q .

In the absence of an external field, the isotropic phase is characterized by Q = 0; the minimum of the free energy also corresponds to Q = 0. This means that, in the Landau expansion of the free energy in terms of the order parameter Q , there is no linear term in Q ; that is,

(2.22)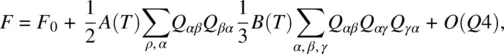

where F 0is a constant and A ( T ) and B ( T ) are temperature‐dependent expansion coefficients:

(2.23)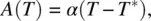

where T * is very close to, but lower than, T c. Typically, .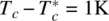

Note that F contains a nonzero term of order Q [3]. This odd function of Q ensures that states with some nonvanishing value of Q (e.g. due to some alignment of molecules) will have different free‐energy values depending on the direction of the alignment. For example, the free energy for a state with an order parameter Q of the form

(2.24a)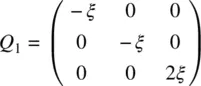

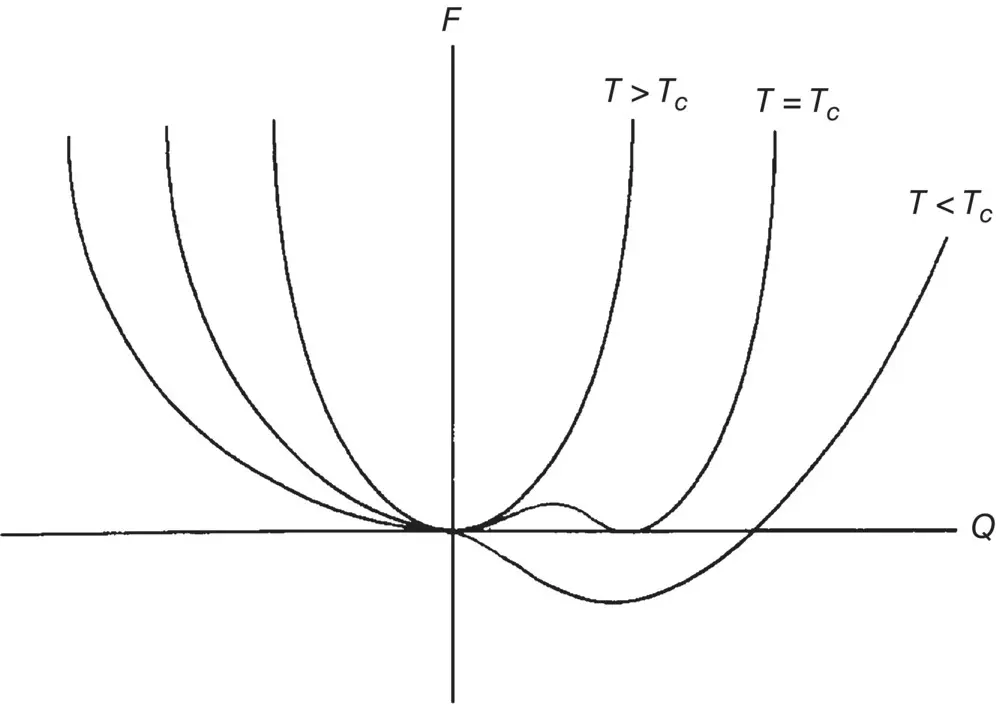
Figure 2.6. Free energies F ( Q ) for different temperatures T . At T = T c, ∂ F/ ∂ Q = 0 at two values of Q , where F has two stable minima. On the other hand, at 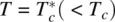, there is only one stable minimum where ∂ F/ ∂ Q = 0.

(i.e. with some alignment of the molecule in the z direction) is not the same as the state with a negative Q parameter

(2.24b)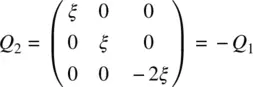

(which signifies some alignment of the molecules in the x ‐ y plane).

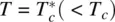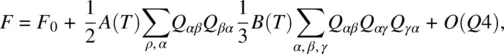
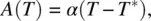
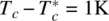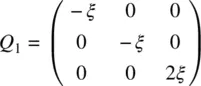
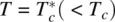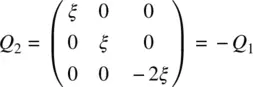
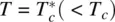The cubic term in F is also important in that it dictates that the phase transition at T = T cis of the first order (i.e. the first‐order derivative of F , ∂ F /∂θ, is vanishing at T = T c, as shown in Figure 2.6). The system has two stable minima, corresponding to Q = 0 or Q ≠ 0 (i.e. the coexistence of the isotropic and nematic phases). On the other hand, for , there is only one stable minimum at Q ≠ 0; this translates into the existence of a single liquid crystalline phase (e.g. nematic or smectic).