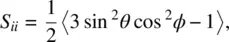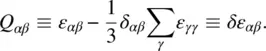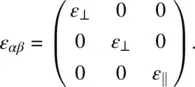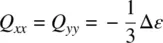51 51. I. C. Khoo, K. L. Hong, S. Zhao, et al. “Blue‐phase liquid crystal cored optical fiber array with photonic bandgaps and nonlinear transmission properties,” Optics Express 21 (4): 4319–4327 (2013).
52 52. C.‐W. Chen, H.‐C. Jau, C.‐T. Wang, et al. “Random lasing in blue phase liquid crystals,” Optics Express 20 (21): 23978–23984 (2012).
2 Order Parameter, Phase Transition, and Free Energies
2.1. BASIC CONCEPTS
2.1.1. Introduction
In the ordered phase, liquid crystals possess both crystalline and fluid properties. The theoretical framework for describing the crystalline properties of liquid crystals, termed elastic or continuum theory, is closer in form to that of solids and invokes similar classical mechanics terminology such as elastic constant, distortion energy, torque, free energies, etc. What makes liquid crystals unique is the fact that in such an ordered phase they also possess many fluidic properties similar to ordinary liquids. Nematic liquid crystals, for example, flow like liquids and thus require hydrodynamical theories for their complete description. These crystalline and flow properties of nematics are explained in further detail in the next chapter.
In the disordered or isotropic phase, they behave like ordinary fluids of anisotropic molecules. They can thus be described by theories pertaining to anisotropic fluids. However, at the vicinity of the isotropic → nematic phase transition point, liquid crystals exhibit some highly correlated pre‐transitional effects such as enhanced but critically slowed response to external fields, owing to increased intermolecular correlations near the phase transition.
In the following sections, we introduce some basic concepts and definitions, such as order parameter, short‐ and long‐range order, phase transition, and so on, which form the basis for describing the ordered and disordered phases of liquid crystals. Most of the discussions pertain to the exemplary nematic liquid crystals. Information on other phases may be found in later chapters and the references quoted therein.
2.1.2. Scalar and Tensor Order Parameters
The physics of liquid crystals is best described in terms of the so‐called order parameters [1, 2]. If we use the long axis of the molecule as a reference and denote it as  , the microscopic scalar order parameter S is defined [1, 2] as follows:
, the microscopic scalar order parameter S is defined [1, 2] as follows:
(2.1) 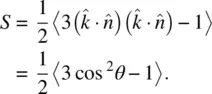
With reference to Figure 2.1, θ is the angle made by the molecular axis with the director axis. The average 〈 〉 is taken over the whole ensemble; this kind of order is usually termed long‐range order. It is called microscopic because it describes the average response of a molecule. The scalar order parameter defined previously is sufficient to describe liquid crystalline systems composed of molecules that possess cylindrical or rotational symmetry around the long axis 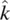 .
.
On the other hand, for molecules lacking such symmetry, or in cases where such rotational symmetry is “destroyed” by the presence of asymmetric dopants or intramolecular material interactions, a more general tensor order parameter S ijis needed. S ijis defined as
(2.2) 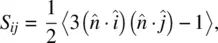
Figure 2.1. Coordinate system defining the microscopic order parameter of a nematic liquid crystal molecule. Here, i , j , and k are the molecular axes, whereas 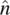 is the laboratory axis that denotes the average direction of liquid crystal alignment.
is the laboratory axis that denotes the average direction of liquid crystal alignment.
where  ,
, 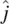 , and
, and 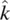 are unit vectors along the molecular axes. With reference to Figure 2.1, the three diagonal components S ii , S jj, and S kkare given by
are unit vectors along the molecular axes. With reference to Figure 2.1, the three diagonal components S ii , S jj, and S kkare given by
(2.3a) 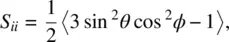
(2.3b) 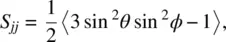
(2.3c) 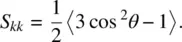
Note that S ii + S jj + S kk = 0. Put another way, S is a traceless tensor because its diagonal elements add up to zero.
For a complete description of the statistical properties of the liquid crystal orientation, functions involving higher powers of cos 2 θ are needed. The most natural functions to use are the Legendre polynomials P 1(cos θ ) ( l = 0, 1, 2,…), in terms of which we can write Eq. (2.1)as S = 〈 P 2〉, which measures the average of cos 2 θ . The next nonvanishing term is 〈 P 4〉, which provides a measure of the dispersion of 〈cos 2 θ 〉.
The order parameters defined previously in terms of the directional averages can be translated into expressions in terms of the anisotropies in the physical parameters such as magnetic, electric, and optical susceptibilities. For example, in terms of the optical dielectric anisotropies Δ ε = ε ‖− ε ⊥, one can define a so‐called macroscopic order parameter that characterizes the bulk response:
(2.4) 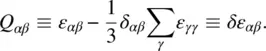
It is called macroscopic because it describes the bulk property of the material. To be more explicit, consider a uniaxial nematic liquid crystal such that in the molecular axis system ε αβis of the form
(2.5) 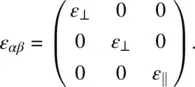
Writing Q αβexplicitly in terms of their diagonal components, we thus have
(2.6) 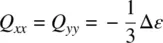
and
Читать дальше

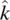 , the microscopic scalar order parameter S is defined [1, 2] as follows:
, the microscopic scalar order parameter S is defined [1, 2] as follows: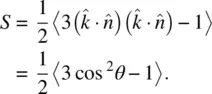
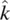 .
.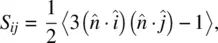

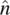 is the laboratory axis that denotes the average direction of liquid crystal alignment.
is the laboratory axis that denotes the average direction of liquid crystal alignment. ,
, 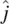 , and
, and 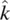 are unit vectors along the molecular axes. With reference to Figure 2.1, the three diagonal components S ii , S jj, and S kkare given by
are unit vectors along the molecular axes. With reference to Figure 2.1, the three diagonal components S ii , S jj, and S kkare given by