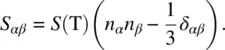2.4.2. Free Energy in the Presence of an Applied Field
In the presence of an externally applied field (e.g. dc or low‐frequency electric, magnetic, or optical electric field), a corresponding interaction term should be added to the free energy.
For an applied magnetic field H , the energy associated with it is
(2.25) 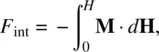
where Mis the magnetization given by
(2.26) 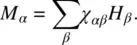
Thus
(2.27) 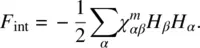
Using Eq. (2.9), we can rewrite F intas
(2.28) 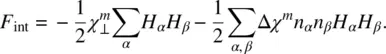
The first term on the right‐hand side of Eq. (2.28)is independent of the orientation of the (anisotropic) molecules, and it can therefore be included in the constant F 0.
On the other hand, the second term is dependent on the orientation of the molecules. Using Eq. (2.10)for the order parameter Q αβwe can write it as
(2.29) 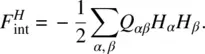
Therefore, the total free energy of a liquid crystal in the isotropic phase, under the action of an externally applied magnetic field, is given by
(2.30) 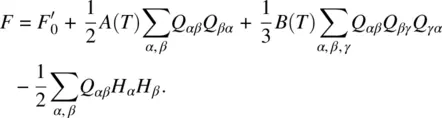
Without solving the problem explicitly, we can infer from the magnetic interaction term that a lower energy state corresponds to some alignment of the molecules in the direction of the magnetic field (for Δ χ m > 0).
Using a similar approach, we can also deduce that the electric interaction contribution to the free energy is given by (in inks units)
(2.31) 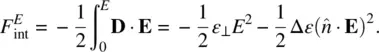
The orientation‐dependent term is therefore
(2.32) 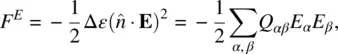
where Q αβis defined in Eq. (2.4).
In Chapter 8, we present a detailed discussion of isotropic phase molecular orientations by an applied optical field from a short intense laser pulse. It is shown that both the response time and the induced order Q depend on the temperature vicinity ( T – T c) in a critical way; they both vary as ( T – T c) −1, which becomes very large near T c. This near‐ T ccritical slowing down behavior of the order parameter Q of the isotropic phase is similar to the slowing down behavior of the order parameter S of the nematic phase discussed in the previous section. Besides the nematic ↔ isotropic phase transition, which is the most prominent order ↔ disorder transition exhibited by liquid crystals, there are other equally interesting phase transition processes among the various mesophases [13], such as smectic‐A ↔ smectic‐C *, which will be discussed in Chapter 4.
1 1. deGennes, P. G. 1974. The Physics of Liquid Crystals. Oxford: Clarendon Press.
2 2. deGennes, P.G. 1971. Mol. Cryst. Liq. Cryst. 12: 193.
3 3. Landau, L. D. 1965. Collected Papers. D. Ter Haar (ed.). New York: Gordon & Breach.
4 4. Litster, J. D. 1971. Critical Phenomena. R. E. Mills (ed.). New York: McGraw‐Hill.
5 5. Khoo, I.C. and S. T. Wu. 1993. Optics and Nonlinear Optics of Liquid Crystals. Singapore: World Scientific.
6 6. See, for example, Blinov, L. M. 1983. Electro‐optical and Magneto‐optical Properties of Liquid Crystals. Chichester: Wiley.
7 7. Maier, W. and A. Saupe. 1959. Z. Naturforsch. 14A: 882; for a concise account of the theory, see Khoo and Wu [5].
8 8. Humphries, R.L., and O. R. Lukhurst. 1972. Chem. Phys. Lett. 17: 514; Luckhurst, G. R., C. Zannoni, P. L. Nordio, et al. 1975. Mol. Phys. 30:1345; Freiser, M. J. 1971. Mol. Cryst. Liq. Cryst. 14: 165.
9 9. Blinov, L.M., V. A. Kizel, V. G. Rumyantsev, et al. 1975. J. Phys. (Paris) Colloq. 36: C1–C69; see also Blinov [6].
10 10. DeJeu, W.H. 1980. Physical Properties of Liquid Crystalline Materials. New York: Gordon and Breach.
11 11. Khoo, I. C., R. G. Lindquist, R. R. Michael, et al. 1991. J. Appl. Phys. 69: 3853.
12 12. Khoo, I.C., and R. Normandin. 1985. IEEE J. Quantum Electron. QE21: 329.
13 13. Chandrasekhar, S. 1992. Liquid Crystals. 2nd ed. Cambridge: Cambridge University Press; see also deGennes [1].
3 Nematic Liquid Crystals
3.1. INTRODUCTION
Nematics best exemplify the dual nature of liquid crystals – fluidity and crystalline structure. To describe their liquid‐like properties, one needs to invoke hydrodynamics. On the other hand, their crystalline properties necessitate theoretical formalisms pertaining to solids or crystals. To study their optical properties, it is also necessary that we invoke individual molecular electronic structures and collective crystalline properties. In this chapter, we discuss all three aspects of nematogen theory: solid‐state continuum theory, hydrodynamics, and electro‐optical properties, in that order.
3.2. ELASTIC CONTINUUM THEORY
3.2.1. The Vector Field: Director Axis
In elastic continuum theory, introduced and refined over the last several decades by several workers [1–3], nematics is basically viewed as crystalline in form. An aligned sample may thus be regarded as a single crystal in which the molecules are, on average, aligned along the direction defined by the director axis  .
.
The crystal is uniaxial and is characterized by a tensorial order parameter:
(3.1) 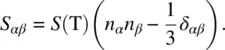
As a result of externally applied fields, stresses/constraints from the boundary surfaces, the director will also vary spatially. The characteristic length over which significant variation in the order parameter will occur, in most cases, is much larger than the molecular size. Typically, for distortions of the form shown in Figure 3.1a–c, the characteristic length is on the order of 1 μm, whereas the molecular dimension is on the order of at most a few tens of angstroms. Under this circumstance, as in other similar systems or media (e.g. ferromagnets), the continuum theory is valid.
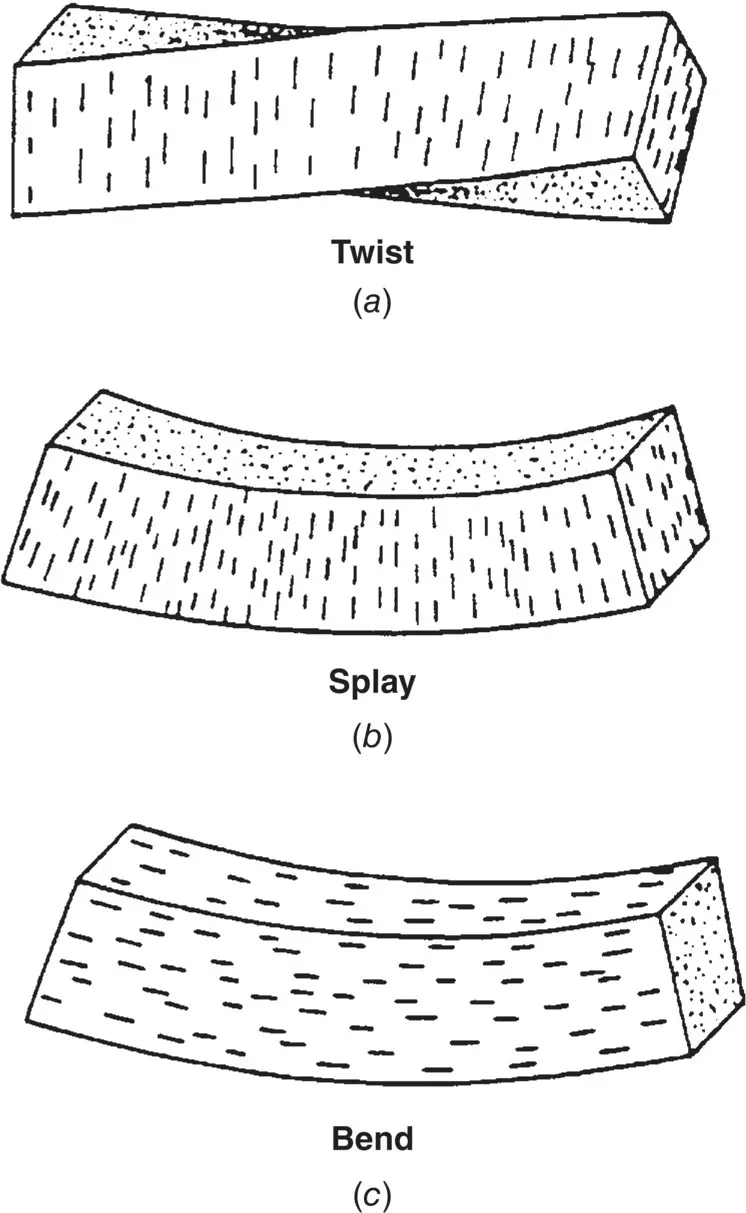
Figure 3.1. (a) Twist deformation in a nematic liquid crystal; (b) splay deformation; (c) bend deformation.
Читать дальше

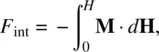
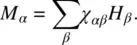
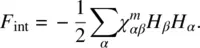
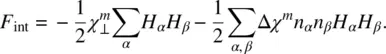
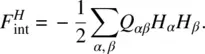
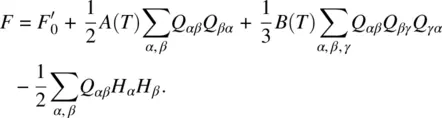
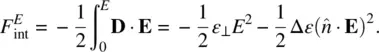
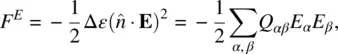
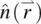 .
.