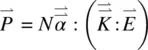3.4.1. Linear Susceptibility and Local Field Effect
In the optical regime, ε ||> ε ⊥. Typically, ε ||is on the order of 2.89 ε 0and ε ⊥is 2.25 ε 0. These correspond to refractive indices n ||= 1.7 and n ⊥= 1.5. An interesting property of nematic liquid crystals is that such a large birefringence (Δ ε ⊥= ε ||− ε ⊥≈ 0.2) is manifested throughout the whole optical spectral regime (from near‐ultraviolet [≈ 400 nm], to visible [≈ 500 nm] and near‐infrared [1–3 μm], to the infrared regime [8–12 μm], i.e. from 400 nm to 12 μm). Figure 3.6shows the measured birefringence of three typical nematic liquid crystals from the UV to the far‐infrared ( λ = 16 μm).
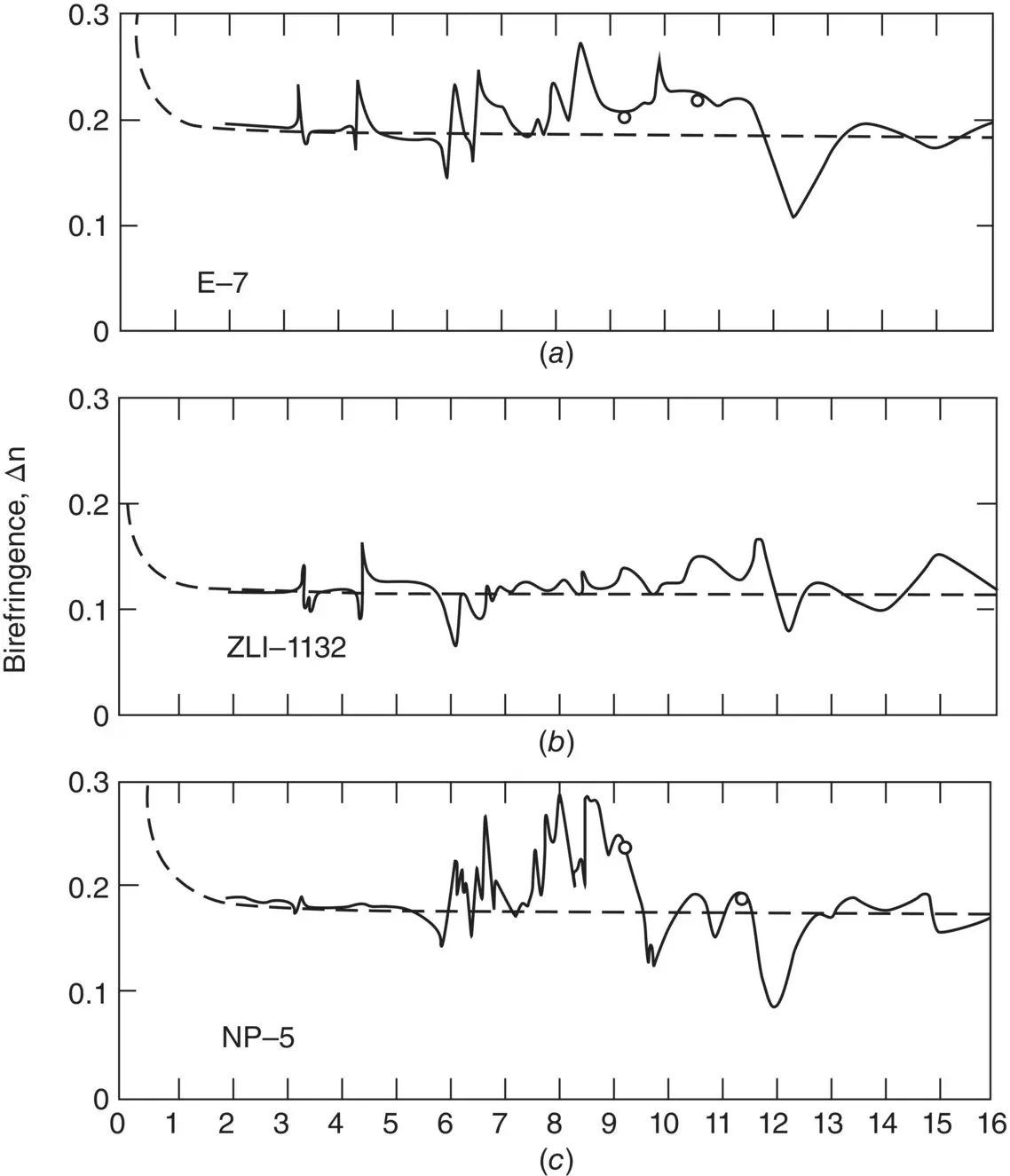
Figure 3.6. Measured birefringence De = ε ||− ε ⊥of three nematic liquid crystals.
The optical dielectric constants originate from the linear polarization 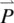 generated by the incident optical field
generated by the incident optical field 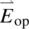 on the nematic liquid crystal:
on the nematic liquid crystal:
(3.30a) 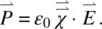
From the defining equation
(3.30b) 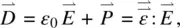
we have
(3.30c) 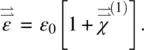
Here 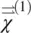 is the linear (sometimes termed “first order”) susceptibility tensor of the nematics.
is the linear (sometimes termed “first order”) susceptibility tensor of the nematics. 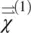 is a macroscopic parameter and is related to the microscopic (molecular) parameter, the molecular polarizabilities tensor α ij, in the following way:
is a macroscopic parameter and is related to the microscopic (molecular) parameter, the molecular polarizabilities tensor α ij, in the following way:
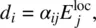
(3.31a) 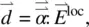
(3.31b) 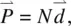
where d iis the i th component of the induced dipole 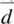 and N is the number density. In Chapter 8, a rigorous quantum mechanical derivation of α in terms of the dipole matrix elements or oscillator strengths and the energy levels and level populations will be presented. The connection between the microscopic parameter α ijand the macroscopic parameter χ ijis the local field correction factor (i.e. the difference between the externally applied field and the actual field as experienced by the molecules). Several theoretical formalisms have been developed to evaluate the field correction factor, ranging from simplified to complex and sophisticated ones.
and N is the number density. In Chapter 8, a rigorous quantum mechanical derivation of α in terms of the dipole matrix elements or oscillator strengths and the energy levels and level populations will be presented. The connection between the microscopic parameter α ijand the macroscopic parameter χ ijis the local field correction factor (i.e. the difference between the externally applied field and the actual field as experienced by the molecules). Several theoretical formalisms have been developed to evaluate the field correction factor, ranging from simplified to complex and sophisticated ones.
Most of the approaches used to obtain the local field correction factor are based on the Lorentz results [5], which state that the internal field (i.e. the local field as experienced by a molecule 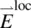 in a solid) is related to the applied field
in a solid) is related to the applied field 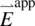 by
by
(3.32a) 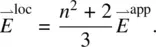
In particular, Vuks [10] analyzed experimental data and proposed that the local field in an anisotropic crystal may be taken as isotropic and expressed in the form
(3.32b) 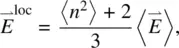
where 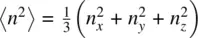 and n x, n y, and n zare the principal refractive indices of the crystal. This approach has been employed in the study of liquid crystals [11]. A more generalized expression for anisotropic crystals is given in Dunmar [12]:
and n x, n y, and n zare the principal refractive indices of the crystal. This approach has been employed in the study of liquid crystals [11]. A more generalized expression for anisotropic crystals is given in Dunmar [12]:
(3.33) 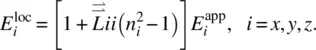
More generally, one can write Eq. (3.33)as
(3.34) 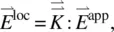
where  , the local field “factor,” is a second‐rank tensor, which states that the local field
, the local field “factor,” is a second‐rank tensor, which states that the local field 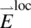 is linearly related to the macroscopic applied field
is linearly related to the macroscopic applied field 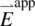 . In general, experimental measurements show that the treatments by Vuks and Dunmar are qualitatively in agreement.
. In general, experimental measurements show that the treatments by Vuks and Dunmar are qualitatively in agreement.
3.4.2. Equilibrium Temperature and Order Parameter Dependences of Refractive Indices
The two principal refractive indices n ⊥and n ||of a uniaxial liquid crystal and the anisotropy n ||− n ⊥have been the subject of intensive studies for their fundamental importance in the understanding of liquid crystal physics and for their vital roles in applied electro‐optic devices. Since the dielectric constants ( ε ⊥and ε ||) enter directly and linearly into the constitutive equations ( Eqs. (3.30a)– (3.30c)), it is theoretically more convenient to discuss the fundamentals of these temperature dependences in terms of the dielectric constants.
From Eq. (3.34)for the local field 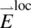 and Eq. (3.31) for the induced dipole moments, we can express the polarization
and Eq. (3.31) for the induced dipole moments, we can express the polarization 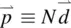 by
by
(3.35) 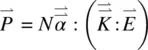
Читать дальше


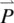 generated by the incident optical field
generated by the incident optical field  on the nematic liquid crystal:
on the nematic liquid crystal: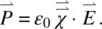
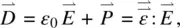
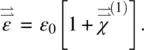
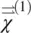 is the linear (sometimes termed “first order”) susceptibility tensor of the nematics.
is the linear (sometimes termed “first order”) susceptibility tensor of the nematics. 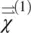 is a macroscopic parameter and is related to the microscopic (molecular) parameter, the molecular polarizabilities tensor α ij, in the following way:
is a macroscopic parameter and is related to the microscopic (molecular) parameter, the molecular polarizabilities tensor α ij, in the following way: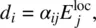
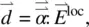
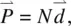
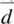 and N is the number density. In Chapter 8, a rigorous quantum mechanical derivation of α in terms of the dipole matrix elements or oscillator strengths and the energy levels and level populations will be presented. The connection between the microscopic parameter α ijand the macroscopic parameter χ ijis the local field correction factor (i.e. the difference between the externally applied field and the actual field as experienced by the molecules). Several theoretical formalisms have been developed to evaluate the field correction factor, ranging from simplified to complex and sophisticated ones.
and N is the number density. In Chapter 8, a rigorous quantum mechanical derivation of α in terms of the dipole matrix elements or oscillator strengths and the energy levels and level populations will be presented. The connection between the microscopic parameter α ijand the macroscopic parameter χ ijis the local field correction factor (i.e. the difference between the externally applied field and the actual field as experienced by the molecules). Several theoretical formalisms have been developed to evaluate the field correction factor, ranging from simplified to complex and sophisticated ones.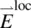 in a solid) is related to the applied field
in a solid) is related to the applied field 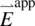 by
by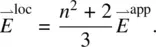
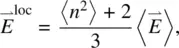
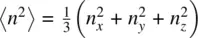 and n x, n y, and n zare the principal refractive indices of the crystal. This approach has been employed in the study of liquid crystals [11]. A more generalized expression for anisotropic crystals is given in Dunmar [12]:
and n x, n y, and n zare the principal refractive indices of the crystal. This approach has been employed in the study of liquid crystals [11]. A more generalized expression for anisotropic crystals is given in Dunmar [12]: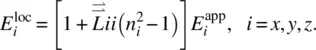
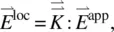
 , the local field “factor,” is a second‐rank tensor, which states that the local field
, the local field “factor,” is a second‐rank tensor, which states that the local field 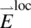 is linearly related to the macroscopic applied field
is linearly related to the macroscopic applied field 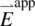 . In general, experimental measurements show that the treatments by Vuks and Dunmar are qualitatively in agreement.
. In general, experimental measurements show that the treatments by Vuks and Dunmar are qualitatively in agreement.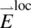 and Eq. (3.31) for the induced dipole moments, we can express the polarization
and Eq. (3.31) for the induced dipole moments, we can express the polarization 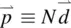 by
by