Equation (3.56), together with Eq. (3.57), forms the basis for studying the hydrodynamics of an isotropic fluid. Note that since the viscosity for 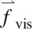 is a spatial derivative of the stress tensor, which in turn is a spatial derivative of the velocity,
is a spatial derivative of the stress tensor, which in turn is a spatial derivative of the velocity, 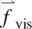 is of the form
is of the form 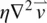 . Equation (3.54), therefore, may be written as
. Equation (3.54), therefore, may be written as
(3.58) 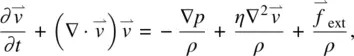
which is usually referred to as the Navier–Stokes equation for an incompressible fluid.
3.5.2. General Stress Tensor for Nematic Liquid Crystals
The general theoretical framework for describing the hydrodynamics of liquid crystals has been developed principally by Leslie [16] and Ericksen [17]. Their approaches account for the fact that the stress tensor depends not only on the velocity gradients but also on the orientation and rotation of the director. Accordingly, the stress tensor is given by
(3.59) 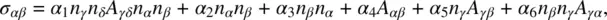
where the A αβs are defined by
(3.60) 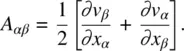
Note that all the other terms on the right‐hand side of Eq. (3.59)involve the director orientation, except the fourth term, α 4 A αβ.This is the same term as that for an isotropic fluid (cf. Eq. [ 3.57]), that is, α 4= 2 η .
Therefore, in this formalism, we have six so‐called Leslie coefficients, α 1, α 2,…, α 6, which have the dimension of viscosity coefficients. It was shown by Parodi [18] that
(3.61) 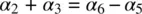
and so there are really five independent coefficients.
In the next few sections, we will study exemplary cases of director axis orientation and deformation, and we will show how these Leslie coefficients are related to other commonly used viscosity coefficients.
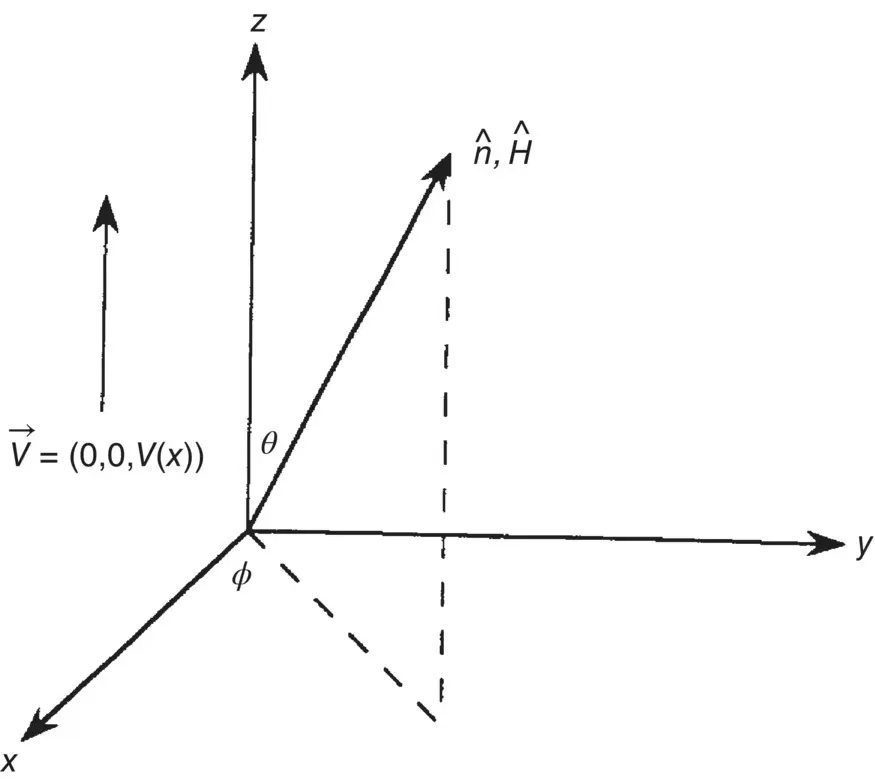
Figure 3.11. Sheer flow in the presence of an applied magnetic field.
3.5.3. Flows with Fixed Director Axis Orientation
Consider here the simplest case of flows in which the director axis orientation is held fixed. This may be achieved by a strong externally applied magnetic field (see Figure 3.11), where the magnetic field is along the direction 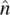 . Consider the case of shear flow, where the velocity is in the z‐ direction, and the velocity gradient is along the x‐ direction. This process could occur, for example, in liquid crystals confined by two parallel plates in the y ‐ z plane.
. Consider the case of shear flow, where the velocity is in the z‐ direction, and the velocity gradient is along the x‐ direction. This process could occur, for example, in liquid crystals confined by two parallel plates in the y ‐ z plane.
In terms of the orientation of the director axis, there are three distinct possibilities involving three corresponding viscosity coefficients:
1 η1: is parallel to the velocity gradient, that is, along the x‐axis (θ = 90°, ϕ = 0°).
2 η2: is parallel to the flow velocity, that is, along the z‐axis and lies in the shear plane x‐z (θ = 0°, ϕ = 0°).
3 η3: is perpendicular to the shear plane, that is, along the y‐axis (θ = 0°, ϕ = 90°).
These three configurations have been investigated by Miesowicz [19], and the η s are known as Miesowicz coefficients. In the original paper, as well as in the treatment by deGennes [3], the definitions of η 1and η 3are interchanged. In deGennes notation, in terms of η a, η b, and η c, we have η a= η 1, η b= η 2, and η c= η 3. The notation used here is attributed to Helfrich [6], which is now the conventional one.
To obtain the relations between η 1,2,3and the Leslie coefficients α 1,2,…,6, one could evaluate the stress tensor σ αβand the shear rate A αβfor various director orientations and flow and velocity gradient directions. From these considerations, the following relationships are obtained [3]:
(3.62) 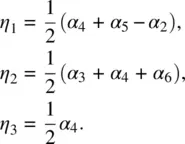
In the shear plane x ‐ z , the general effective viscosity coefficient is actually more correctly expressed in the form [20]
(3.63) 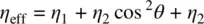
in order to account for angular velocity gradients. The coefficient η 1,2is related to the Leslie coefficient α 1by
(3.64) 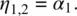
3.5.4. Flows with Director Axis Reorientation
The preceding section deals with the case where the director axis is fixed during fluid flow. In more general situations, director axis reorientation often accompanies fluid flows and vice versa. Taking into account the moment of inertia I and the torque 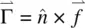 , where
, where 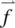 is the molecular internal elastic field defined in Eq. (3.11),
is the molecular internal elastic field defined in Eq. (3.11), 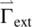 is the torque associated with an externally applied field, and
is the torque associated with an externally applied field, and 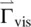 is the viscous torque associated with the viscous forces, the equation of motion describing the angular acceleration d Ω/ dt as the director axis may be written as
is the viscous torque associated with the viscous forces, the equation of motion describing the angular acceleration d Ω/ dt as the director axis may be written as
(3.65) 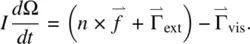
The viscous torque 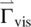 consists of two components [3]: one arising from pure rotational effect (i.e. no coupling to the fluid flow) given by
consists of two components [3]: one arising from pure rotational effect (i.e. no coupling to the fluid flow) given by  and another arising from coupling to the fluid motion given by
and another arising from coupling to the fluid motion given by 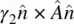 . Therefore, we have
. Therefore, we have
Читать дальше

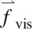 is a spatial derivative of the stress tensor, which in turn is a spatial derivative of the velocity,
is a spatial derivative of the stress tensor, which in turn is a spatial derivative of the velocity, 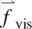 is of the form
is of the form 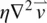 . Equation (3.54), therefore, may be written as
. Equation (3.54), therefore, may be written as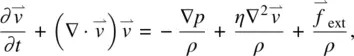
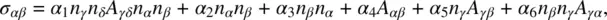
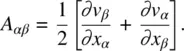
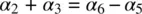

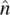 . Consider the case of shear flow, where the velocity is in the z‐ direction, and the velocity gradient is along the x‐ direction. This process could occur, for example, in liquid crystals confined by two parallel plates in the y ‐ z plane.
. Consider the case of shear flow, where the velocity is in the z‐ direction, and the velocity gradient is along the x‐ direction. This process could occur, for example, in liquid crystals confined by two parallel plates in the y ‐ z plane.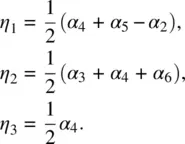
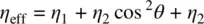
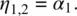
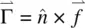 , where
, where 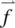 is the molecular internal elastic field defined in Eq. (3.11),
is the molecular internal elastic field defined in Eq. (3.11), 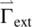 is the torque associated with an externally applied field, and
is the torque associated with an externally applied field, and 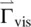 is the viscous torque associated with the viscous forces, the equation of motion describing the angular acceleration d Ω/ dt as the director axis may be written as
is the viscous torque associated with the viscous forces, the equation of motion describing the angular acceleration d Ω/ dt as the director axis may be written as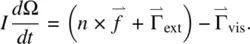
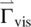 consists of two components [3]: one arising from pure rotational effect (i.e. no coupling to the fluid flow) given by
consists of two components [3]: one arising from pure rotational effect (i.e. no coupling to the fluid flow) given by  and another arising from coupling to the fluid motion given by
and another arising from coupling to the fluid motion given by 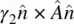 . Therefore, we have
. Therefore, we have










