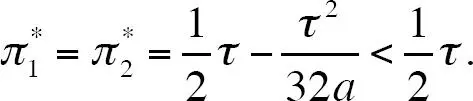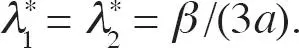
Se sigue que 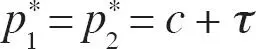 como en el modelo inicial de Hotelling. Como ambas empresas escogen la misma intensidad publicitaria, incrementan la disposición del consumidor a pagar por su producto de forma simétrica y, por lo tanto, se neutralizan entre sí: la publicidad no afecta los precios de equilibrio. Los beneficios de equilibrio se calculan como
como en el modelo inicial de Hotelling. Como ambas empresas escogen la misma intensidad publicitaria, incrementan la disposición del consumidor a pagar por su producto de forma simétrica y, por lo tanto, se neutralizan entre sí: la publicidad no afecta los precios de equilibrio. Los beneficios de equilibrio se calculan como

Las empresas están peor debido a su habilidad para realizar publicidad persuasiva. Como en el modelo con publicidad informativa, las empresas le darían la bienvenida a un aumento en los costos de la publicidad (un a mayor) o a una reducción en el “poder persuasivo” de la publicidad (un β menor). En realidad, si las empresas pudieran cooperar en la etapa en que se hace publicidad, la evitarían del todo. De hecho, actuando cooperativamente, enfrentarían el siguiente programa de maximización:
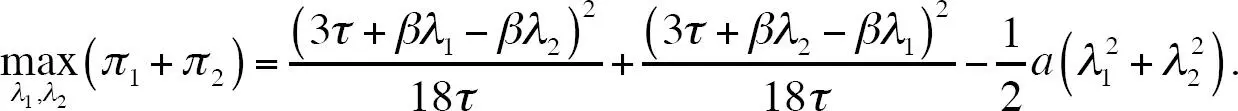
Evaluando la condición de primer orden en intensidades publicitarias simétricas se obtiene
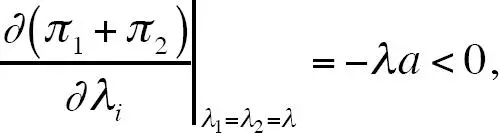
Lo que significa que la decisión óptima es λ 1= λ 2= 0. En este último resultado podemos encontrar una segunda explicación al por qué algunas asociaciones profesionales respaldan las prohibiciones a la publicidad para su profesión. [57]
La publicidad cambia la distribución de las preferencias de los consumidores
Una empresa también puede usar la publicidad persuasiva para amoldar las preferencias de los consumidores, para poder convencerlos de que lo que realmente necesitan es su producto y no el de la competencia. Para capturar esta idea en el modelo, dejamos que la publicidad transforme la distribución uniforme inicial de los consumidores en una distribución diferente. Para ser precisos, tomamos la siguiente función de distribución simétrica:
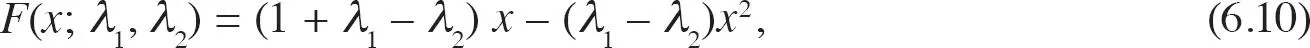
con densidad continua
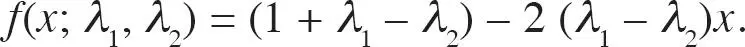
Si las dos empresas tienen el mismo gasto en publicidad λ , mantenemos la distribución uniforme inicial: F ( x ; λ , λ ) = x y f ( x ; λ , λ ) = 1. Si la empresa 1 hace más publicidad que la 2, λ 1> λ 2, entonces tenemos una distribución cóncava, sesgada hacia la empresa 1. A su vez, si λ 1< λ 2, entonces la distribución es convexa y sesgada hacia la empresa 2. Por ejemplo, la densidad f ( x ; 1,0) = 2 – 2 x favorece a la empresa 1, mientras que la densidad f ( x ; 0,1) = 2 x favorece a la empresa 2.
La demanda para la empresa 1 está dada por 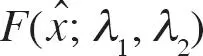 y la demanda para la empresa 2 por 1 −
y la demanda para la empresa 2 por 1 − 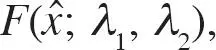 donde
donde 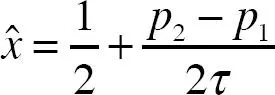 identifica al consumidor indiferente. Usando la expresión ( 6.10), tenemos
identifica al consumidor indiferente. Usando la expresión ( 6.10), tenemos
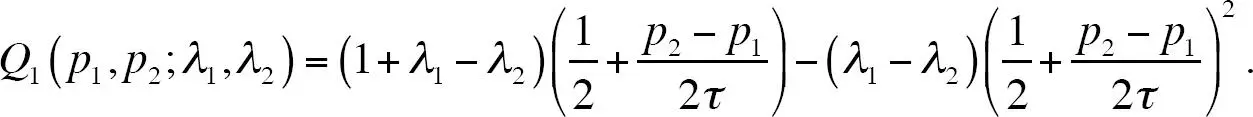
Debido a la complejidad relativa de esta última función de demanda, aquí consideramos que las empresas escogen intensidades publicitarias y precios simultáneamente, e invocamos la simetría para simplificar considerablemente el problema. La empresa 1 resuelve el siguiente programa de maximización:
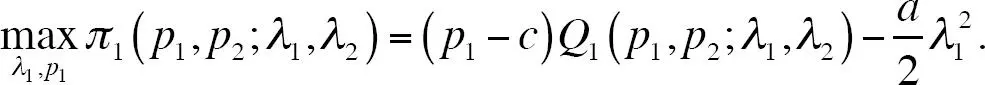
La condición de primer orden respecto a p 1es

En el equilibrio simétrico, λ 1= λ 2= λ , lo que implica que  Se sigue que las funciones de reacción son exactamente iguales a las del modelo de Hotelling, produciendo los precios de equilibrio usuales,
Se sigue que las funciones de reacción son exactamente iguales a las del modelo de Hotelling, produciendo los precios de equilibrio usuales, 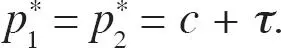 La condición de primer orden respecto a λ 1es
La condición de primer orden respecto a λ 1es
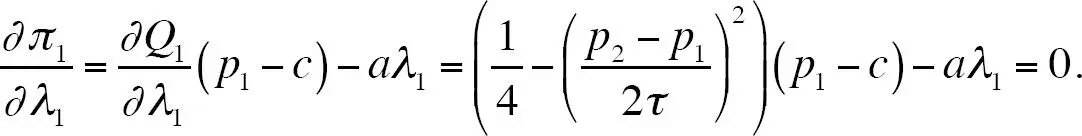
Utilizando el hecho de que 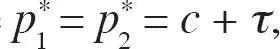 podemos reescribir la última ecuación como
podemos reescribir la última ecuación como 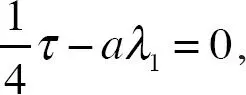 lo que implica que
lo que implica que 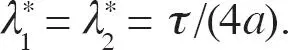 [58]
[58]
Como en el caso en el que la publicidad incrementa la disposición a pagar, las dos empresas hacen publicidad, pero terminan neutralizándose entre sí. Por lo tanto, los gastos en publicidad son un mero costo para las empresas, que están atrapadas en un dilema del prisionero. Los beneficios de equilibrio son (suponiendo que 4 a > τ para garantizar beneficios positivos)
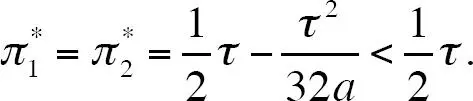
De los dos casos que acabamos de analizar podemos extraer la siguiente lección.
Читать дальше

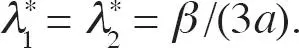
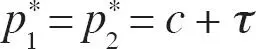 como en el modelo inicial de Hotelling. Como ambas empresas escogen la misma intensidad publicitaria, incrementan la disposición del consumidor a pagar por su producto de forma simétrica y, por lo tanto, se neutralizan entre sí: la publicidad no afecta los precios de equilibrio. Los beneficios de equilibrio se calculan como
como en el modelo inicial de Hotelling. Como ambas empresas escogen la misma intensidad publicitaria, incrementan la disposición del consumidor a pagar por su producto de forma simétrica y, por lo tanto, se neutralizan entre sí: la publicidad no afecta los precios de equilibrio. Los beneficios de equilibrio se calculan como
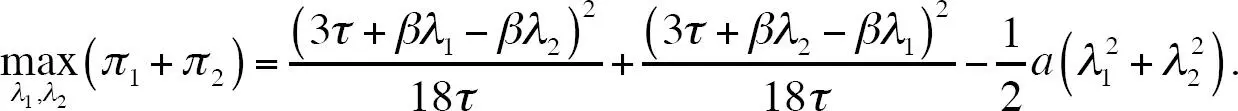
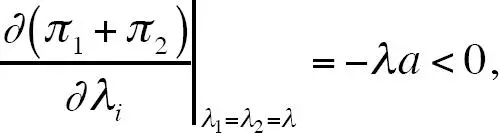
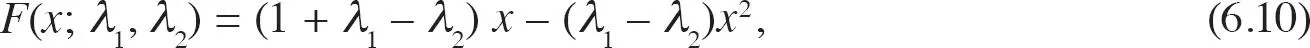
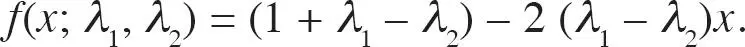
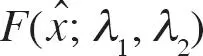 y la demanda para la empresa 2 por 1 −
y la demanda para la empresa 2 por 1 − 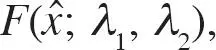 donde
donde 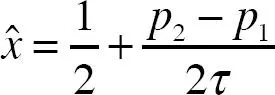 identifica al consumidor indiferente. Usando la expresión ( 6.10), tenemos
identifica al consumidor indiferente. Usando la expresión ( 6.10), tenemos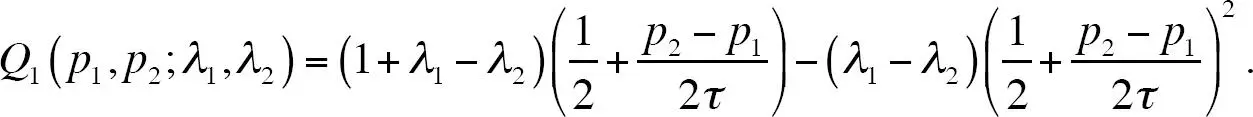
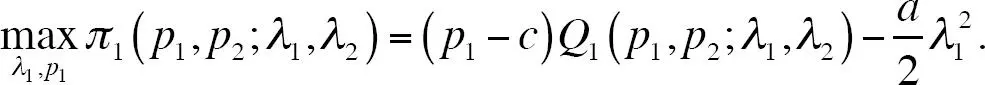

 Se sigue que las funciones de reacción son exactamente iguales a las del modelo de Hotelling, produciendo los precios de equilibrio usuales,
Se sigue que las funciones de reacción son exactamente iguales a las del modelo de Hotelling, produciendo los precios de equilibrio usuales, 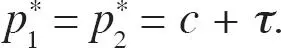 La condición de primer orden respecto a λ 1es
La condición de primer orden respecto a λ 1es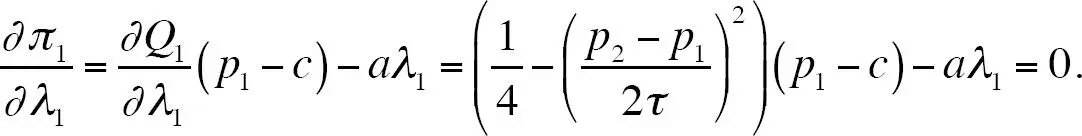
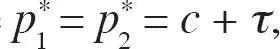 podemos reescribir la última ecuación como
podemos reescribir la última ecuación como 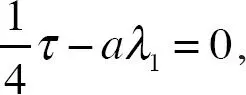 lo que implica que
lo que implica que 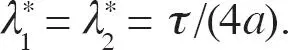 [58]
[58]