Formalizamos esta intuición con ayuda del modelo de Hotelling con costos lineales de transporte, en el que dos empresas están localizadas en los puntos extremos del intervalo unitario. [50]Hay una masa unitaria de consumidores distribuidos uniformemente en este intervalo. La notación se mantiene: un consumidor x tiene una utilidad u = r – τx – p 1si compra una unidad del bien 1 y u = r – τ (1 – x ) – p 2si compra una unidad del bien 2. Entre los consumidores que tienen información sobre ambos productos, hay un consumidor indiferente que está dado por
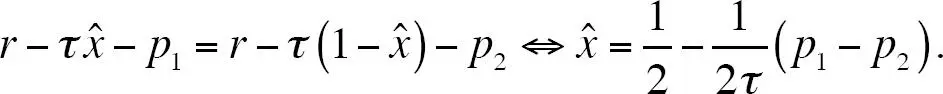
Entonces, si todos los consumidores conocen ambos productos, la demanda para el bien 1 sería
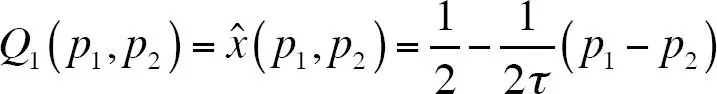
y la demanda para el bien 2, 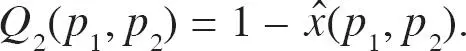
Sin embargo, solamente una proporción λi de consumidores conoce la existencia del producto i . Suponemos que la probabilidad de que un consumidor tenga esta información es independiente de la ubicación, de modo que la publicidad no es focalizada y es independiente de si un consumidor conoce el producto del competidor. Entonces, hay λi λj consumidores que conocen la existencia de ambos bienes. Los consumidores de este grupo tienen información completa. Hay λi (1 – λj )consumidores que solamente conocen la existencia del producto i , pero no del producto j .
Por lo tanto, hay tres tipos de consumidores: consumidores con información completa que conocen ambos productos, consumidores con información parcial que conocen uno de los productos y consumidores sin información que no conocen ninguno de los productos. Los consumidores sin información no compran. Los consumidores con información parcial deben decidir si compran el bien que conocen: en el caso en que un consumidor conoce el bien i , compra si r – τ – pi ≥ 0. Por simplicidad, suponemos que r es lo suficientemente grande como para garantizar que la última desigualdad se cumple, lo que significa que individualmente es racional para todos los consumidores comprar al menos uno de los bienes.
Las empresas fijan simultáneamente los precios y el número de anuncios publicitarios. Para informar a una proporción λi de consumidores sobre la existencia, características y precio del producto i , una empresa incurre en costos A ( λi ), A ′ > 0, A ″ > 0. Por simplicidad, suponemos que A toma la forma cuadrática 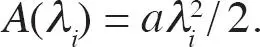 Si la publicidad estuviera asociada con costos bajos, las empresas informarían a todos los consumidores. Para excluir esta posibilidad, suponemos que a < τ /2.
Si la publicidad estuviera asociada con costos bajos, las empresas informarían a todos los consumidores. Para excluir esta posibilidad, suponemos que a < τ /2.
Por lo tanto, (1 – λ 1) (1 – λ 2) es la proporción de consumidores desinformados, λ 1(1 – λ 2) la proporción de consumidores informados sobre el producto 1 pero no sobre el 2, λ 2(1 – λ 1) la proporción de consumidores informados sobre el producto 2 pero no sobre el 1, λ 1 λ 2es la proporción de consumidores con información completa. Entonces, la demanda de la empresa 1 tiene la forma
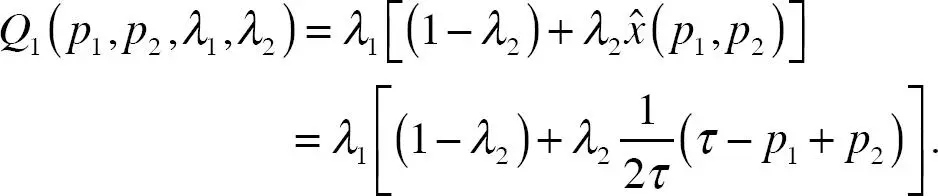
De forma similar para la empresa 2. La figura 6.1muestra la demanda de las dos empresas. La parte superior de la figura identifica al consumidor indiferente 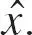 La demanda entre los consumidores que conocen ambos productos se divide de forma correspondiente.
La demanda entre los consumidores que conocen ambos productos se divide de forma correspondiente.
Figura 6.1 Demanda con publicidad informativa
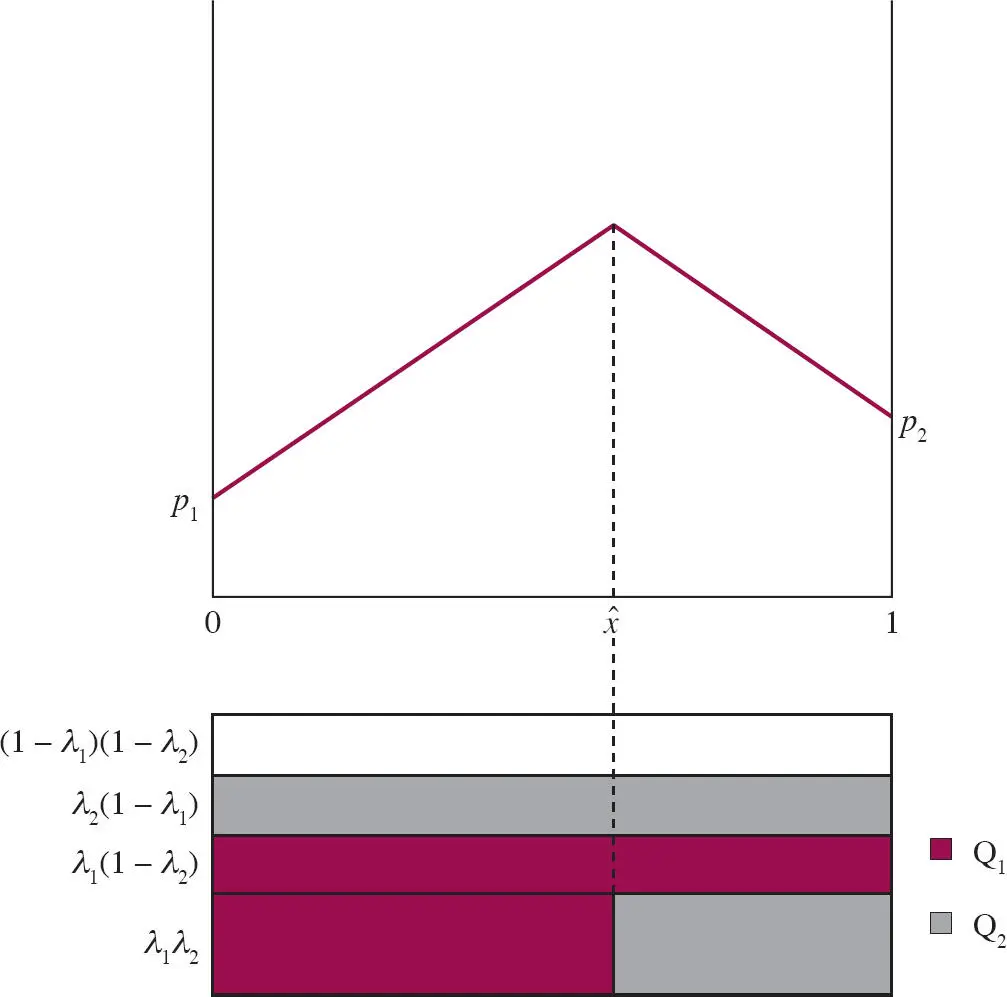
Una mayor cantidad de publicidad informativa por parte de ambas empresas conduce primero a una proporción mayor de consumidores con información completa. Esto implica, como mostramos a continuación, que una mayor cantidad de publicidad informativa aumenta la elasticidad precio de la demanda (lo que confirma la predicción de la perspectiva informativa). Consideremos una situación simétrica, es decir, p 1= p 2≡ p y λ 1= λ 2≡ λ . La elasticidad precio de la demanda es
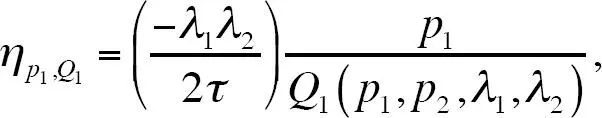
que evaluada en precios simétricos se convierte en
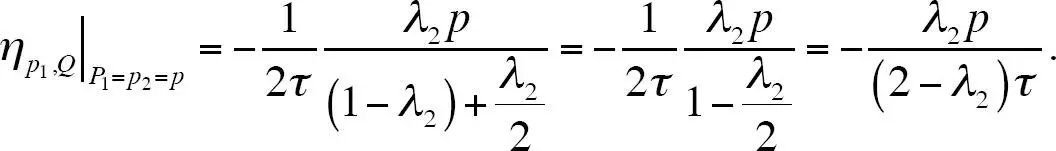
Fijemos λ = λ 2. Entonces, un aumento en la publicidad informativa, que lleva a una mayor proporción de consumidores informados sobre cada producto, aumenta la elasticidad precio de la demanda, ( ∂ | ηp, Q |)/( ∂λ ) > 0. La razón está en que, a medida que λ aumenta, los segmentos sin un competidor se vuelven más pequeños respecto a los segmentos con un competidor, lo que conduce a una competencia más intensa.
Ahora pasamos al análisis del equilibrio. El problema de maximización de la empresa 1 es
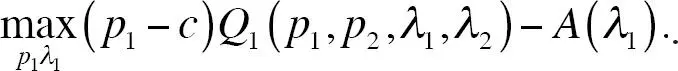
De forma correspondiente para la empresa 2. Caracterizamos el equilibrio de Nash en estrategias puras. Recuerde que un equilibrio de Nash 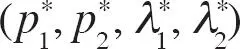 satisface
satisface
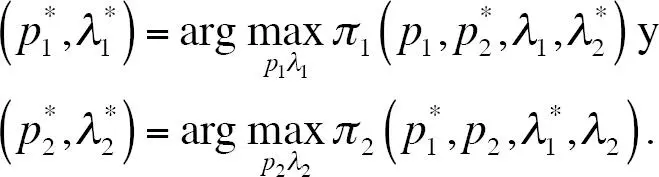
Las condiciones de primer orden de la maximización de beneficios pueden escribirse como
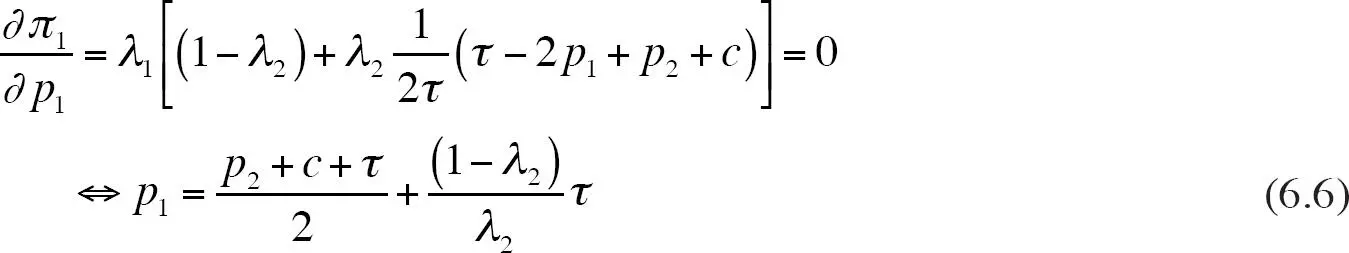
y
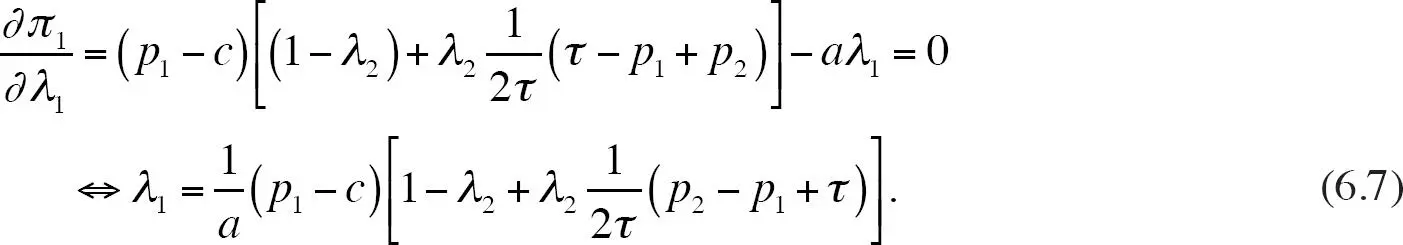
Respecto a la reacción del precio tal como está dada por la ecuación ( 6.6), recuerde que 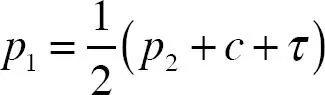 es la función de reacción si todos los consumidores estuvieran informados. Por tanto, si λj < 1, entonces la empresa i fija un precio más alto dado pj que con información completa para todos los consumidores. Esto quiere decir que la elasticidad de la demanda es menor que con información completa. Respecto a la reacción de la publicidad tal como está dada por la ecuación ( 6.7), note que el costo marginal de la publicidad, a λ 1, es igual al ingreso marginal de la publicidad, donde este último es simplemente el producto del margen de beneficios pi – c y la probabilidad de que se realice una venta.
es la función de reacción si todos los consumidores estuvieran informados. Por tanto, si λj < 1, entonces la empresa i fija un precio más alto dado pj que con información completa para todos los consumidores. Esto quiere decir que la elasticidad de la demanda es menor que con información completa. Respecto a la reacción de la publicidad tal como está dada por la ecuación ( 6.7), note que el costo marginal de la publicidad, a λ 1, es igual al ingreso marginal de la publicidad, donde este último es simplemente el producto del margen de beneficios pi – c y la probabilidad de que se realice una venta.
Читать дальше

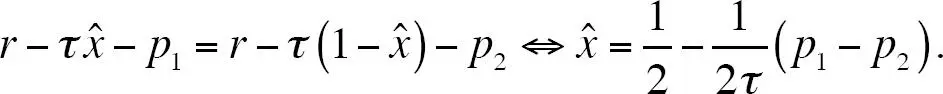
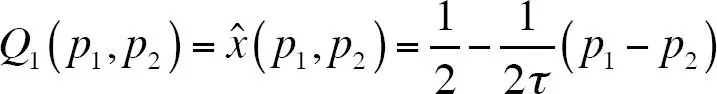
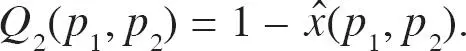
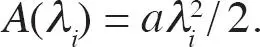 Si la publicidad estuviera asociada con costos bajos, las empresas informarían a todos los consumidores. Para excluir esta posibilidad, suponemos que a < τ /2.
Si la publicidad estuviera asociada con costos bajos, las empresas informarían a todos los consumidores. Para excluir esta posibilidad, suponemos que a < τ /2.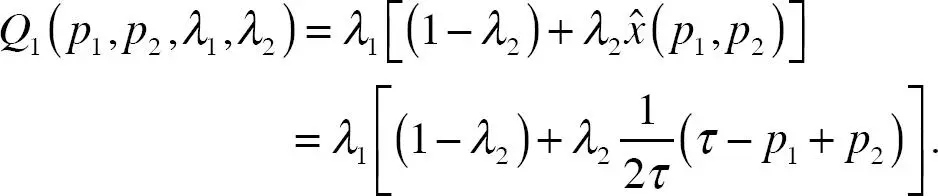
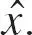 La demanda entre los consumidores que conocen ambos productos se divide de forma correspondiente.
La demanda entre los consumidores que conocen ambos productos se divide de forma correspondiente.
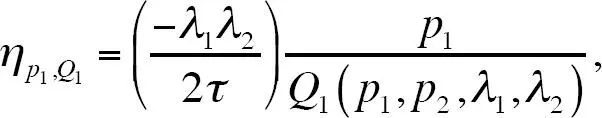
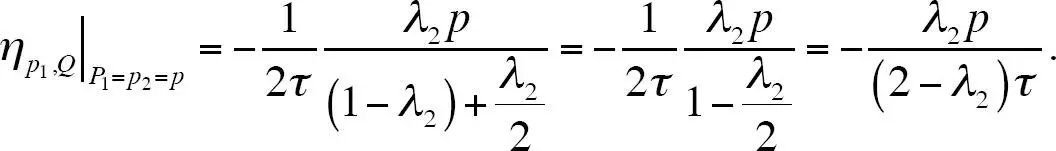
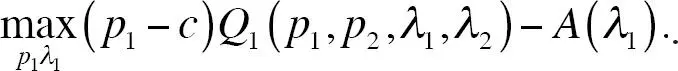
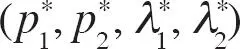 satisface
satisface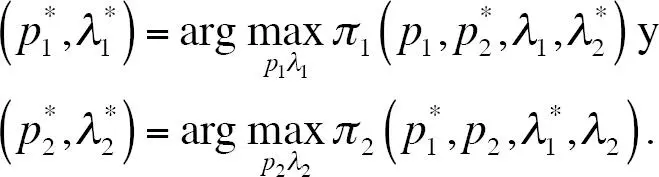
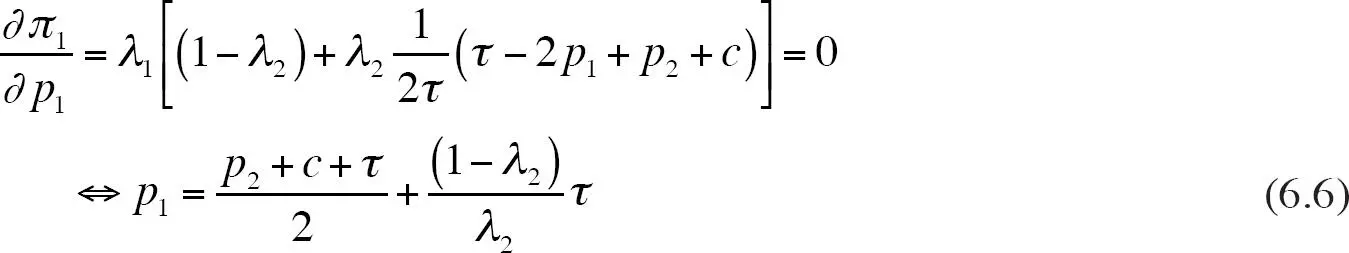
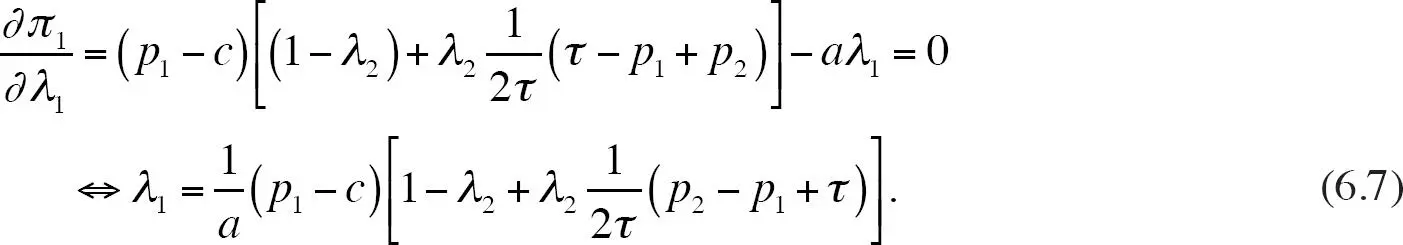
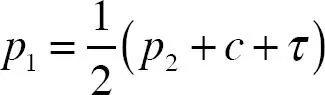 es la función de reacción si todos los consumidores estuvieran informados. Por tanto, si λj < 1, entonces la empresa i fija un precio más alto dado pj que con información completa para todos los consumidores. Esto quiere decir que la elasticidad de la demanda es menor que con información completa. Respecto a la reacción de la publicidad tal como está dada por la ecuación ( 6.7), note que el costo marginal de la publicidad, a λ 1, es igual al ingreso marginal de la publicidad, donde este último es simplemente el producto del margen de beneficios pi – c y la probabilidad de que se realice una venta.
es la función de reacción si todos los consumidores estuvieran informados. Por tanto, si λj < 1, entonces la empresa i fija un precio más alto dado pj que con información completa para todos los consumidores. Esto quiere decir que la elasticidad de la demanda es menor que con información completa. Respecto a la reacción de la publicidad tal como está dada por la ecuación ( 6.7), note que el costo marginal de la publicidad, a λ 1, es igual al ingreso marginal de la publicidad, donde este último es simplemente el producto del margen de beneficios pi – c y la probabilidad de que se realice una venta.