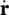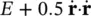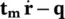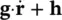Its drawback lies in the fact that in the presence of saturated and unsaturated states, the stress tensor changes between the two states; when the pore air is absent, the constitutive equations for saturated states cannot be recovered from those for unsaturated states without additional control (Sheng et al. 2004). This precludes practically its application in soil dynamics; capturing liquefaction becomes a problem.
The compressibility of the solid grains was also considered by Khalili et al. (2000) in their stress tensor
(2.54) 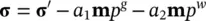
where a 1, a 2are the effective stress parameters defined as 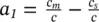 ,
, 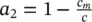 , c sis the grain compressibility, c the drained compressibility of the soil structure, and c mthe tangent compressibility of the soil structure with respect to a change in capillary pressure.
, c sis the grain compressibility, c the drained compressibility of the soil structure, and c mthe tangent compressibility of the soil structure with respect to a change in capillary pressure.
In the following, we make use of (2.51)with the assumption that solid grains are incompressible, i.e. α = 1. The governing equations are derived again, using the hybrid mixture theory, as has been done by Schrefler (1995) and Lewis and Schrefler (1998). Isothermal conditions are assumed to hold, as throughout this book. For the full non‐isothermal case, the interested reader is referred to Lewis and Schrefler (1998) and Schrefler (2002).
We first recall briefly the kinematics of the system.
2.5.1 Kinematic Equations
As indicated in Chapter 1, a multiphase medium can be described as the superposition of all π phases, π = 1, 2, … , κ, i.e. in the current configuration, each spatial point xis simultaneously occupied by material points X πof all phases. The state of motion of each phase is however described independently.
In a Lagrangian or material description of motion, the position of each material point x πat time t is a function of its placement in a chosen reference configuration, X πand of the current time t
(2.55) 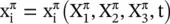
To keep this mapping continuous and bijective at all times, the determinant of the Jacobian of this transformation must not equal zero and must be strictly positive, since it is equal to the determinant of the deformation gradient tensor F π
(2.56) 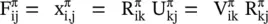
where U πis the right stretch tensor, V πthe left stretch tensor, and the skew‐symmetric tensor R πgives the rigid body rotation. Differentiation with respect to the appropriate coordinates of the reference or actual configuration is respectively denoted by comma or slash, i.e.
(2.57) 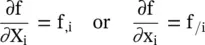
Because of the non‐singularity of the Lagrangian relationship (2.55), its inverse can be written and the Eulerian or spatial description of motion follows
(2.58) 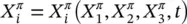
The material time derivative of any differentiable function f π( X, t) given in its spatial description and referred to a moving particle of the π phase is
(2.59) 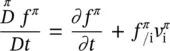
If superscript α is used for 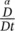 , the time derivative is taken moving with the α phase.
, the time derivative is taken moving with the α phase.
2.5.2 Microscopic Balance Equations
In the hybrid mixture theories, the microscopic situation of any π phase is first described by the classical equations of continuum mechanics. At the interfaces to other constituents, the material properties and thermodynamic quantities may present step discontinuities. As throughout the book, the effects of the interfaces are here not taken into account explicitly. These are introduced, e.g. in Schrefler (2002) and Gray and Schrefler (2001, 2007).
For a thermodynamic property ψ , the conservation equation within the π phase may be written as
(2.60) 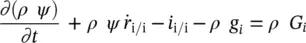
where 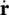 is the local value of the velocity field of the π phase in a fixed point in space, iis the flux vector associated with Ψ , gthe external supply of Ψ , and Gis the net production of Ψ . The relevant thermodynamic properties Ψ are mass, momentum, energy, and entropy. The values assumed by i, g, and Gare given in Table 2.2(Hassanizadeh and Gray 1980, 1990; Schrefler 1995). The constituents are assumed to be microscopically nonpolar; hence, the angular momentum balance equation has been omitted. This equation shows, however, that the stress tensor is symmetric.
is the local value of the velocity field of the π phase in a fixed point in space, iis the flux vector associated with Ψ , gthe external supply of Ψ , and Gis the net production of Ψ . The relevant thermodynamic properties Ψ are mass, momentum, energy, and entropy. The values assumed by i, g, and Gare given in Table 2.2(Hassanizadeh and Gray 1980, 1990; Schrefler 1995). The constituents are assumed to be microscopically nonpolar; hence, the angular momentum balance equation has been omitted. This equation shows, however, that the stress tensor is symmetric.
Table 2.2 Thermodynamic properties for the microscopic mass balance equations.
Sources: Adapted from Hassanizadeh and Gray (1980, 1990), and Schrefler (1995).
| Quantity |
ψ |
i |
g |
G |
| Mass |
1 |
0 |
0 |
0 |
| Momentum |
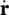 |
t m |
g |
0 |
| Energy |
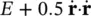 |
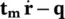 |
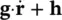 |
0 |
| Entropy |
Λ |
Φ |
S |
φ |
2.5.3 Macroscopic Balance Equations
For isothermal conditions, as here assumed, the macroscopic balance equations for mass, linear momentum, and angular momentum are then obtained by systematically applying the averaging procedures to the microscopic balance Equation (2.60)as outlined in Hassanizadeh and Gray (1979a, 1979b, 1980). The balance equations have here been specialized for a deforming porous material, where the flow of water and of moist air (mixture of dryair and vapor) is taking place (see Schrefler 1995).
Читать дальше

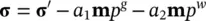
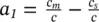 ,
, 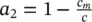 , c sis the grain compressibility, c the drained compressibility of the soil structure, and c mthe tangent compressibility of the soil structure with respect to a change in capillary pressure.
, c sis the grain compressibility, c the drained compressibility of the soil structure, and c mthe tangent compressibility of the soil structure with respect to a change in capillary pressure.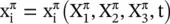
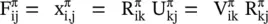
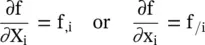
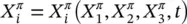
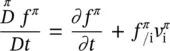
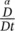 , the time derivative is taken moving with the α phase.
, the time derivative is taken moving with the α phase.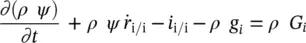
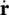 is the local value of the velocity field of the π phase in a fixed point in space, iis the flux vector associated with Ψ , gthe external supply of Ψ , and Gis the net production of Ψ . The relevant thermodynamic properties Ψ are mass, momentum, energy, and entropy. The values assumed by i, g, and Gare given in Table 2.2(Hassanizadeh and Gray 1980, 1990; Schrefler 1995). The constituents are assumed to be microscopically nonpolar; hence, the angular momentum balance equation has been omitted. This equation shows, however, that the stress tensor is symmetric.
is the local value of the velocity field of the π phase in a fixed point in space, iis the flux vector associated with Ψ , gthe external supply of Ψ , and Gis the net production of Ψ . The relevant thermodynamic properties Ψ are mass, momentum, energy, and entropy. The values assumed by i, g, and Gare given in Table 2.2(Hassanizadeh and Gray 1980, 1990; Schrefler 1995). The constituents are assumed to be microscopically nonpolar; hence, the angular momentum balance equation has been omitted. This equation shows, however, that the stress tensor is symmetric.