Manuel Pastor - Computational Geomechanics

Similarly, the mass balance equation for air becomes

(2.88)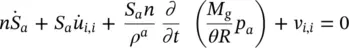

where again the first of Equation (2.86)has been taken into account and the gradient of water density has been neglected. Similar remarks as for the water mass balance equation apply. In particular, the constitutive relationships for moist air, Equations (2.70)and (2.71), have been used.

Finally, if, for the solid phase, the following constitutive relationship is used (viz. Lewis and Schrefler 1998)

(2.89)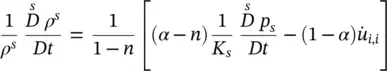

where K sis the bulk modulus of the grain material, then the mass balance equations are obtained in the same form as in Section 2.4(with χ w= S w), though this is not in agreement with what was assumed here for the effective stress.

As this section does not follow the notations use of the book, we summarize below for purposes of nomenclature:

aπmass averaged acceleration of π phase aπsacceleration relative to the solid bexternal momentum supply 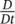material time derivativeEspecific intrinsic energyFπdeformation gradient tensorfπdifferentiable functionf/i∂f/∂xif,i∂f/∂Xi gexternal momentum supply related to gravitational effects Gnet production of thermodynamic property Ψhintrinsic heat sourceiflux vector associated with thermodynamic property Ψ constitutive coefficient Kintrinsic permeability tensor Krπrelative permeability of π phase kπdynamic permeability tensorKwwater bulk modulus 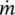mass rate of water evaporationMπmolar mass of constituent πnporositypccapillary pressurepgadry air pressure pgwvapor pressurepaair pressurepssolid pressurepwpressure of liquid waterpπmacroscopic pressure of the π phase 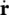local value of the velocity fieldRuniversal gas constant Rconstitutive tensor Rπrigid body rotation tensorSintrinsic entropy sourceSwdegree of water saturationSadegree of air saturationtcurrent time tmmicroscopic stress tensor tπpartial stress tensor πexchange of momentum due to mechanical interaction of the π phase with other phases 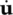mass averaged solid phase velocity Uπright stretch tensor vπsvelocity of the π phase with respect to the solid phase vwmass averaged water velocity vamass averaged air velocity vvolume averaged water relative velocity wvolume averaged air relative velocity Vπleft stretch tensor xπmaterial point Xπreference configuration εlinear strain tensorΦentropy fluxφincrease of entropyηπvolume fraction of the π phaseχwBishop parameterλspecific entropyμπdynamic viscosityθπabsolute temperature of constituent πρaveraged density of the multi‐phase mediumρπintrinsic phase averaged density of the π phaseρπphase averaged density of the π phaseρmicroscopic density σ′effective stress tensorΨgeneric thermodynamic property or variable

ga =dry airgw =vapora =airw =waters =solid

The equations derived in this chapter together with appropriately defined constitutive laws allow (almost) all geomechanical phenomena to be studied. In Chapter 3, we shall discuss in some detail approximation by the finite element method leading to their solution.

1 Biot, M. A. (1941). General theory of three‐dimensional consolidation, J. Appl. Phys., 12, 155–164.

2 Biot, M. A. (1955). Theory of elasticity and consolidation for a porous anisotropic solid, J. Appl. Phys., 26, 182–185.

3 Biot, M. A. (1956a). Theory of propagation of elastic waves in a fluid‐saturated porous solid, Part I: Low‐frequency range, J. Acoust. Soc. Am., 28, 2, 168–178.

4 Biot, M. A. (1956b). Theory of propagation of elastic waves in a fluid‐saturated porous solid, Part II: Low‐frequency range, J. Acoust. Soc. Am., 28, 2, 179–191.

5 Biot, M. A. (1962). Mechanics of deformation and acoustic propagation in porous media, J. Appl. Phys., 33, 4, 1482–1498.

6 Biot, M. A. and Willis, P. G. (1957). The elastic coefficients of the theory consolidation, J. Appl. Mech., 24, 594–601.

7 Bishop, A. W. (1959). The principle of effective stress, Teknisk Ukeblad, 39, 859–863.

8 Bolzon, G., Schrefler, B. A. (1995). State surfaces of partially saturated soils: an effective pressure approach. Appl. Mech. Rev., 48 (10), 643–649.

9 Borja, R. I. (2004). Cam‐Clay plasticity. Part V: A mathematical framework for three‐phase deformation and strain localization analyses of partially saturated porous media. Comp. Methods Appl. Mech. Eng., 193, 5301–5338.

10 Bowen, R. M. (1976). Theory of Mixtures in Continuum Physics, Academic Press, New York.

11 Bowen, R. M. (1980). Incompressible porous media models by use of the theory of mixtures, Int. J. Eng. Sci. 18, 1129–1148.

12 Bowen, R. M. (1982). Compressible porous media models by use of theories of mixtures, Int. J. Eng. Sci. 20, 697–735.

13 Chan, A. H. C., Famiyesin, O. O., and Muir Wood, D. (1991). A fully explicit u‐w schemes for dynamic soil and pore fluid interaction. Asian Pacific Conference on Computational Mechanics, Hong Kong, Vol. 1, Balkema, Rotterdam, 881–887 (11–13 December 1991).

14 Coussy, O. (1995). Mechanics of Porous Media, John Wiley & Sons, Chichester.

15 Coussy, O. (2004). Poromechanics, John Wiley & Sons, Chichester.

16 Craig, R. F. (1992). Soil Mechanics (5), Chapman & Hall, London.

17 De Boer, R. (1996). Highlights in the historical development of the porous media theory, Appl. Mech. Rev., 49, 201–262.

18 De Boer, R. and Kowalski, S. J. (1983). A plasticity theory for fluid saturated porous solids, Int. J. Eng. Sci., 21, 1343–1357.

19 De Boer, R., Ehlers, W., Kowalski, S. and Plischka, J. (1991). Porous Media, a Survey of Different Approaches, Forschungsbericht aus dem Fachbereich Bauwesen, 54, Universitaet‐Gesamthochschule Essen.

20 Derski, W. (1978). Equations of motion for a fluid saturated porous solid, Bull. Acad. Polish Sci. Tech., 26, 11–16.

21 Desai, C. S. (1977a). Discussion—Finite element, residual schemes for unconfined flow, Int. J. Numer. Methods Eng., 11, 80–81.

22 Desai, C. S. (1977b). Finite element, residual schemes for unconfined flow, Int. J. Numer. Methods Eng. 10, 1415–1418.