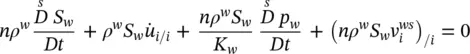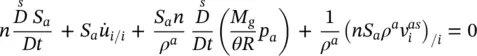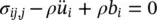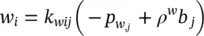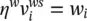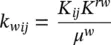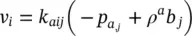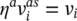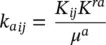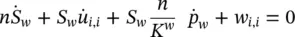It is assumed that R πis invertible, its inverse being 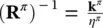 and k πis defined by the following relation:
and k πis defined by the following relation:
(2.73) 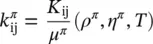
where μ πis the dynamic viscosity with dimensions [mass] [length] −1[time] −1, K the intrinsic permeability [length] 2and T the temperature above some datum. The permeability of (2.73)is the dynamic permeability [length] 3[mass] −1[time]; to obtain the soil mechanics permeability k′ [length]/[time], Equation (2.73)has to be multiplied by the specific weight of water γ wof dimensions [mass] [length] −2[time] −2. In the case of more than one fluid flowing, the intrinsic permeability is modified as
(2.74) 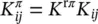
where K rπis the relative permeability, a function of the degree of saturation. For the water density, the following holds:
(2.75) 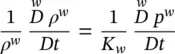
where K wis the bulk modulus of water.
2.5.5 General Field Equations
The macroscopic balance laws are now transformed and the constitutive equations introduced, to obtain the general field equations.
The linear momentum balance equation for the fluid phases is obtained first. In Equation (2.65), the fluid acceleration is expressed, taking into account Equation (2.59), and introducing the relative fluid acceleration a πs. Further, Equations (2.67)and (2.68)are introduced. The terms dependent on the gradient of the fluid velocity and the effects of phase change are neglected and a vector identity for the divergence of the stress tensor is used. Finally, Equations (2.73)and (2.74)are included, yielding
(2.76) 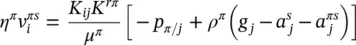
The linear momentum balance equation for the solid phase is obtained in a similar way, taking into account Equations (2.68)instead of (2.67).
By summing this momentum balance equation with Equation (2.76)written for water and air and by taking into account the definition of total stress (2.69), assuming continuity of stress at the fluid‐solid interfaces and by introducing the averaged density of the multiphase medium
(2.77) 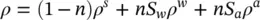
we obtain the linear momentum balance equation for the whole multiphase medium
(2.78) 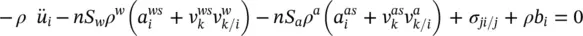
The mass balance equations are derived next.
The macroscopic mass balance equation for the solid phase (2.61), after differentiation and dividing by ρ sis obtained as
(2.79) 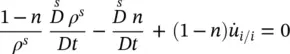
This equation is used in the subsequent mass balance equations to eliminate the material time derivative of the porosity. For incompressible grains, as assumed here, 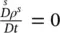 . For compressible grains, see Equation (2.89)and related remarks.
. For compressible grains, see Equation (2.89)and related remarks.
The mass balance equation for water (2.63)is transformed as follows. First in Equation (2.75), the material time derivative of the water density with respect to the moving solid phase and the relative velocity v wsare introduced. Then the derivatives are carried out, the quantity of water lost through evaporation is neglected and the material time derivative of the porosity is expressed through Equation (2.79), yielding
(2.80) 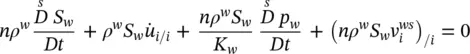
The mass balance equation for air is derived in a similar way
(2.81) 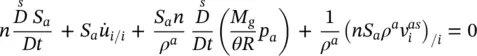
To obtain the equations of Section 2.4.2, further simplifications are needed, which are introduced next.
An updated Lagrangian framework is used where the reference configuration is the last converged configuration of the solid phase. Further, the strain increments within each time step are small. Because of this, we can neglect the convective terms in all the balance equations. Neglecting in the linear momentum balance Equation (2.78)further the relative accelerations of the fluid phases with respect to the solid phase yields the equilibrium Equation (2.34a)
(2.82) 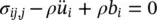
The linear momentum balance equation for fluids (2.76)by omitting all acceleration terms, as in Section 2.2.2, can be written for water
(2.83) 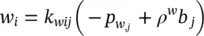
where
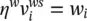
and
(2.84) 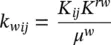
and for air
(2.85) 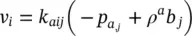
where
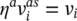
and
(2.86) 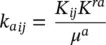
The phase densities appearing in Sections 2.2– 2.4are intrinsic phase averaged densities as indicated above.
The mass balance equation for water is obtained from Equation (2.80), taking into account the reference system chosen, dividing by ρ w, developing the divergence term of the relative velocity and neglecting the gradient of water density. This yields
(2.87) 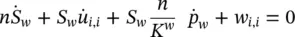
where the first of Equation (2.84)has been taken into account. This coincides with Equation (2.41a)for incompressible grains ( α = 1) except for the source term and the second‐order term due to the change in fluid density. This last one could be introduced in the constitutive relationship (2.75).
Читать дальше

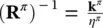 and k πis defined by the following relation:
and k πis defined by the following relation: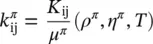
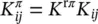
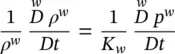
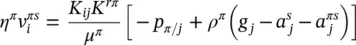
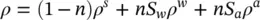
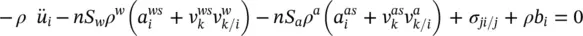
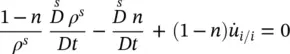
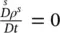 . For compressible grains, see Equation (2.89)and related remarks.
. For compressible grains, see Equation (2.89)and related remarks.