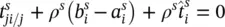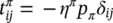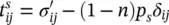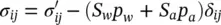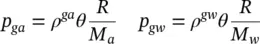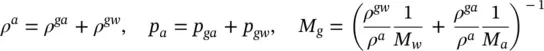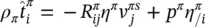The local thermodynamic equilibrium hypothesis is assumed to hold because the time scale of the modeled phenomena is substantially larger than the relaxation time required reaching equilibrium locally. The temperatures of each constituent in a generic point are hence equal. Further, the constituents are assumed to be immiscible and chemically nonreacting. All fluids are assumed to be in contact with the solid phase. As throughout this book, stress is defined as tension positive for the solid phase, while pore pressure is defined as compressively positive for the fluids.
In the averaging procedure, the volume fractions η πappear which are identified as follows: for solid phase η s= 1 − n , for water η w= nS w, and for air η a= nS a.
The averaged macroscopic mass balance equations are given next. For the solid phase, this equation reads
(2.61) 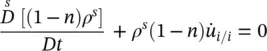
where 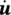 is the mass averaged solid phase velocity and ρ πis the intrinsic phase averaged density. The intrinsic phase averaged density ρ πis the density of the π phase averaged over the part of the control volume (Representative Elementary Volume, REV) occupied by the π phase. The phase averaged density ρ π, on the contrary, is the density of the π phase averaged over the total control volume. The relationship between the two densities is given by
is the mass averaged solid phase velocity and ρ πis the intrinsic phase averaged density. The intrinsic phase averaged density ρ πis the density of the π phase averaged over the part of the control volume (Representative Elementary Volume, REV) occupied by the π phase. The phase averaged density ρ π, on the contrary, is the density of the π phase averaged over the total control volume. The relationship between the two densities is given by
(2.62) 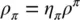
For water, the averaged macroscopic mass balance equation reads
(2.63) 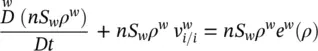
where 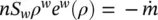 is the quantity of water per unit time and volume, lost through evaporation and v wthe mass averaged water velocity.
is the quantity of water per unit time and volume, lost through evaporation and v wthe mass averaged water velocity.
For air, this equation reads
(2.64) 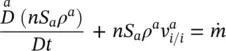
where v ais the mass averaged air velocity.
The linear momentum balance equation for the fluid phases is
(2.65) 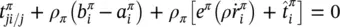
where t πis the partial stress tensor, ρ π b πthe external momentum supply due to gravity, ρ π a πthe volume density of the inertia force, 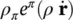 the sum of the momentum supply due to averaged mass supply, and the intrinsic momentum supply due to a change of density and referred to the deviation
the sum of the momentum supply due to averaged mass supply, and the intrinsic momentum supply due to a change of density and referred to the deviation 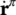 of the velocity of constituent π from its mass averaged velocity, and
of the velocity of constituent π from its mass averaged velocity, and 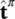 accounts for exchange of momentum due to mechanical interaction with other phases.
accounts for exchange of momentum due to mechanical interaction with other phases. 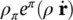 is assumed to be different from zero only for fluid phases. For the solid phase, the linear momentum balance equation is hence
is assumed to be different from zero only for fluid phases. For the solid phase, the linear momentum balance equation is hence
(2.66) 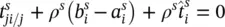
The average angular momentum balance equation shows that for nonpolar media, the partial stress tensor is symmetric t π ji= t π tjat the macroscopic level also and the sum of the coupling vectors of angular momentum between the phases vanishes.
2.5.4 Constitutive Equations
Constitutive models are selected here which are based on quantities currently measurable in laboratory or field experiments and which have been extensively validated. Most of them have been obtained from entropy inequality; see Hassanizadeh and Gray (1980, 1990).
It can be shown that the stress tensor in the fluid is
(2.67) 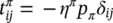
where p πis the fluid pressure, and in the solid phase is
(2.68) 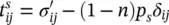
with p s= p w S w+ p a S ain the case of thermodynamic equilibrium or for incompressible solid grains (2.50).
The sum of (2.67), written for air and water and of (2.68), gives the total stress σ , acting on a unit area of the volume fraction mixture
(2.69) 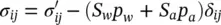
This is the form of the effective stress (2.51), also called generalized Bishop stress (Nuth and Laloui 2008), employed in the following, as already explained.
Moist air in the pore system is assumed to be a perfect mixture of two ideal gases, dry air and water vapour, with π = ga and π = gw , respectively. The equation of a perfect gas is hence valid
(2.70) 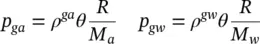
where M πis the molar mass of constituent π , R the universal gas constant, and θ the common absolute temperature. Further, Dalton’s law applies and yields the molar mass of moisture
(2.71) 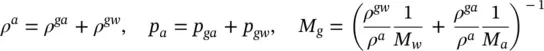
Water is usually present in the pores as a condensed liquid, separated from its vapor by a concave meniscus because of surface tension. The capillary pressure is defined as p c= p g− p w, see Equation (2.43).
The momentum exchange term of the linear momentum balance equation for fluids has the form
(2.72) 
where v πsis the velocity of the π phase relative to the solid.
Читать дальше

 is the mass averaged solid phase velocity and ρ πis the intrinsic phase averaged density. The intrinsic phase averaged density ρ πis the density of the π phase averaged over the part of the control volume (Representative Elementary Volume, REV) occupied by the π phase. The phase averaged density ρ π, on the contrary, is the density of the π phase averaged over the total control volume. The relationship between the two densities is given by
is the mass averaged solid phase velocity and ρ πis the intrinsic phase averaged density. The intrinsic phase averaged density ρ πis the density of the π phase averaged over the part of the control volume (Representative Elementary Volume, REV) occupied by the π phase. The phase averaged density ρ π, on the contrary, is the density of the π phase averaged over the total control volume. The relationship between the two densities is given by
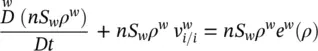
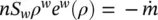 is the quantity of water per unit time and volume, lost through evaporation and v wthe mass averaged water velocity.
is the quantity of water per unit time and volume, lost through evaporation and v wthe mass averaged water velocity.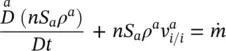
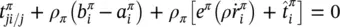
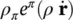 the sum of the momentum supply due to averaged mass supply, and the intrinsic momentum supply due to a change of density and referred to the deviation
the sum of the momentum supply due to averaged mass supply, and the intrinsic momentum supply due to a change of density and referred to the deviation 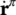 of the velocity of constituent π from its mass averaged velocity, and
of the velocity of constituent π from its mass averaged velocity, and 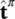 accounts for exchange of momentum due to mechanical interaction with other phases.
accounts for exchange of momentum due to mechanical interaction with other phases. 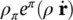 is assumed to be different from zero only for fluid phases. For the solid phase, the linear momentum balance equation is hence
is assumed to be different from zero only for fluid phases. For the solid phase, the linear momentum balance equation is hence