Manuel Pastor - Computational Geomechanics

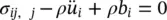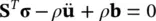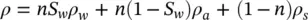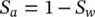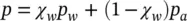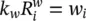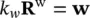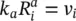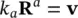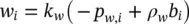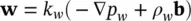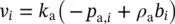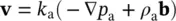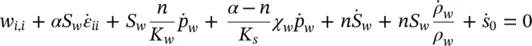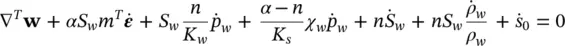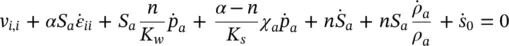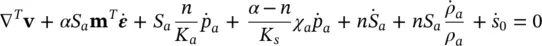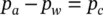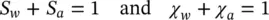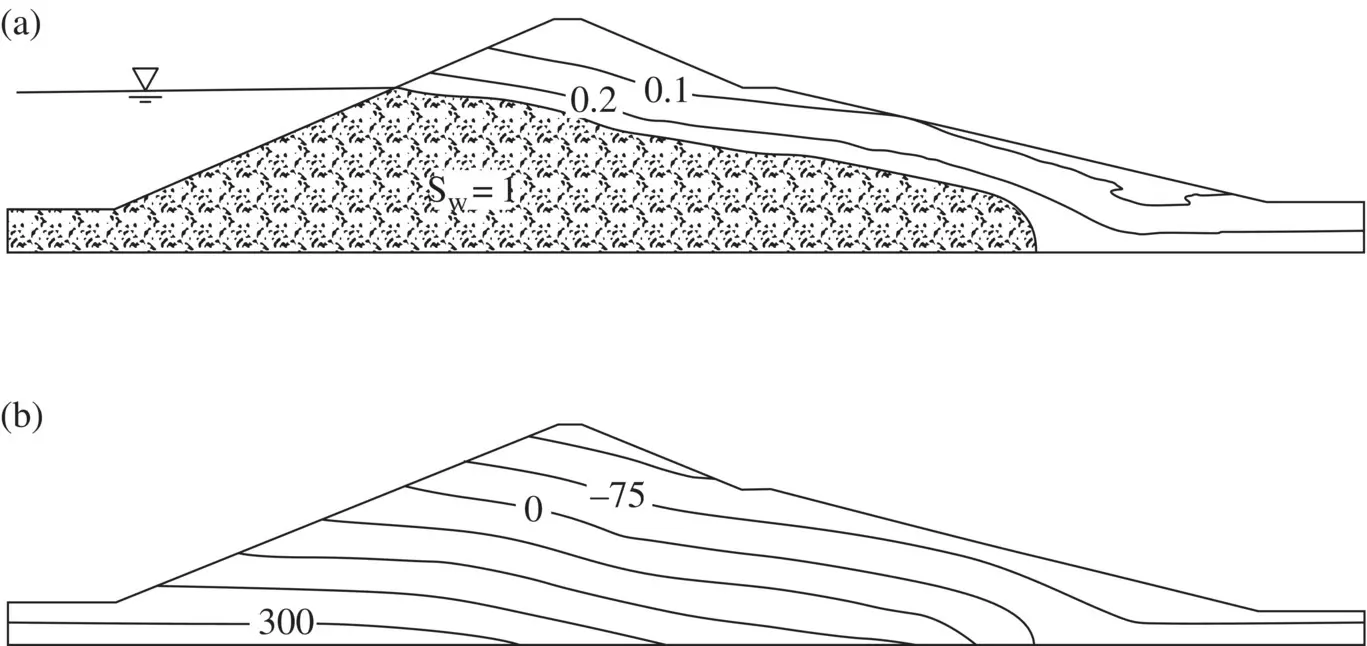
Figure 2.3 A partially saturated dam. Initial steady‐state solution. Only saturation (a) and pressure contours (b) are shown. Contour interval in (b) is 75 kPa. The Phreatic line is the boundary of the fully saturated zone in (a)

Figure 2.4 Test example of partially saturated flow experiment by Liakopoulos (1965). (a) Configuration of test (uniform inflow interrupted at t = 0); (b) pressures with – – –, computed; ––––––, recorded; (c) data (linear elastic analysis, E = 3000 kPa).

Source: From Liakopoulos (1965)

In the practical code used for earthquake analysis, we shall use this partially saturated flow to calculate a wide range of soil mechanics phenomena. However, for completeness in Section 2.4, we shall show how the effects of air movement can be incorporated into the analysis.

This part of the chapter is introduced for completeness – though the effects of the air pressure are insignificant in most problems. However, in some cases of consolidation and confined materials, the air pressures play an important role and it is useful to have means for their prediction. Further, the procedures introduced are readily applicable to other pore–fluid mixtures. For instance, the simultaneous presence of water and oil is important in some areas of geomechanics and coupled problems are of importance in the treatment of hydrocarbon reservoirs. The procedures used in the analysis follow precisely the same lines as introduced here.

In particular, the treatment following the physical approach used in this chapter has been introduced by Simoni and Schrefler (1991), Li et al. (1990) and Schrefler and Zhan (1993) for the flow of water with air.

The alternative approach of using the mixture theory in these problems was outlined by Li and Zienkiewicz (1992) and Schrefler (1995).

Some simple considerations will allow the basic equations for the dynamics of the soil containing two pore fluids to be derived. They have been solved by Schrefler and Scotta (2001) and an example will be shown in Section 8.5.

The dynamics of the total mixture can, just as in Section 2.3, be written in precisely the same form as that for a single fluid phase (see (2.11)). For completeness, we repeat that equation here (now, however, a priori omitting the small convective terms)

(2.34a)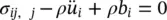

(2.34b)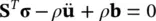

However, just as in Equation (2.25), we have to write

(2.35)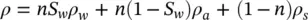

noting that

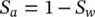
For definition of effective stress, we again use ( 2.24) now, however, without equating the air pressure to zero, i.e. writing

(2.36)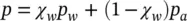

For the flow of water and air, we can write the Darcy equations separately, noting that

(2.37a)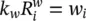

(2.37b)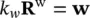

for water as in (2.27) and for the flow of air:

(2.38a)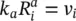

(2.38b)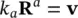

Here we introduced appropriate terms for coefficients of permeability for water and air, while assuming isotropy. A new variable vnow defines the air velocity.

The approximate momentum conservation Equation (see 2.13) can be rewritten in a similar manner using isotropy but omitting acceleration terms for simplicity. We therefore have for water

(2.39a)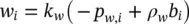

(2.39b)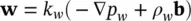

and for air

(2.40a)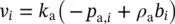

(2.40b)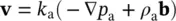

Finally, the mass balance equations for both water and air have to be written. These are derived in a manner identical to that used for Equation (2.30). Thus, for water, we have

(2.41a)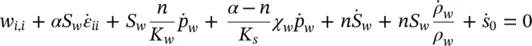

(2.41b)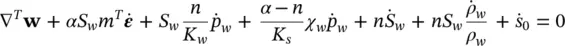

and for air

(2.42a)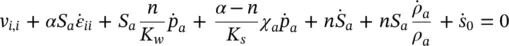

or

(2.42b)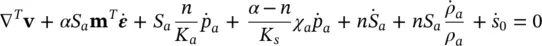

Now, in addition to the solid phase displacement u i( u), we have to consider the water pressure p wand the air pressure p aas independent variables.

However, we note that now (see (1.21))

(2.43)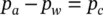

and that the relation between p cand S Wis unique and of the type shown in Figure 1.6. p cnow defines S Wand from the fact that

(2.44)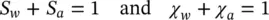

air saturation can also be found.

We have now the complete equation system necessary for dealing with the flow of air and water (or any other two fluids) coupled with the solid phase deformation.