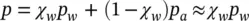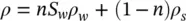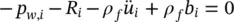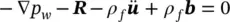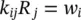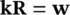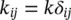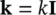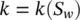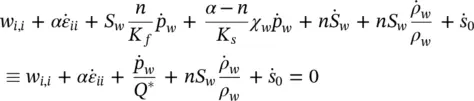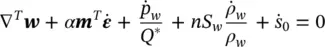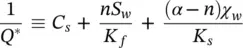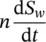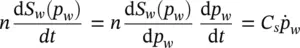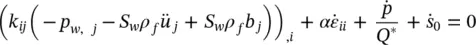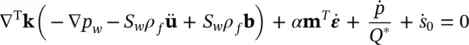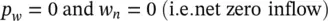Manuel Pastor - Computational Geomechanics

The necessary modification of Equations (2.20) and (2.21) will be derived below, noting that generally we shall consider partial saturation only in the slower phenomena for which u– p approximation is permissible.

Before proceeding, we must note that the effective stress definition is modified and the effective pressure now becomes (viz Section 1.3.3)

(2.24)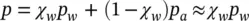

with the effective stress still defined by (2.1).

Equation (2.20) remains unaltered in form whether or not the material is saturated but the overall density ρ is slightly different now. Thus in place of ( 2.12), we can write

(2.25)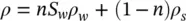

neglecting the weight of air. The correction is obviously small and its effect insignificant.

However, (2.21) will now appear in a modified form which we shall derive here.

First, the water momentum equilibrium, Equation (2.13), will be considered. We note that its form remains unchanged but with the variable p being replaced by p w. We thus have

(2.26a)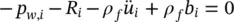

(2.26b)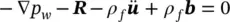

As before, we have neglected the relative acceleration of the fluid to the solid.

Equation (2.14), defining the permeabilities, remains unchanged as

(2.27a)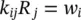

(2.27b)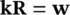

However, in general, only scalar, i.e. isotropic, permeability will be used here

(2.28a)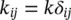

(2.28b)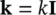

where Iis the identity matrix. The value of k is, however, dependent strongly on S wand we note that:

(2.29)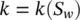

Such typical dependence is again shown in Figure 1.6.

Finally, the conservation Equation (2.16) has to be restructured, though the reader will recognize similarities.

The mass balance will once again consider the divergence of fluid flow w i,ito be augmented by terms previously derived (and some additional ones). These are

1 Increased pore volume due to change of strain assuming no change of saturation: δijdεij = dεii

2 An additional volume stored by compression of the fluid due to fluid pressure increase: nSwdpw/Kf

3 Change of volume of the solid phase due to fluid pressure increase: (1 − n)χwdpw/Ks

4 Change of volume of solid phase due to change of intergranular contact stress: −KT/Ks(dεii + χwdpw/Ks)

5 And a new term taking into account the change of saturation: ndSw

Adding to the above, as in Section 2.2, the terms involving density changes, on thermal expansion, the conservation equation now becomes:

(2.30a)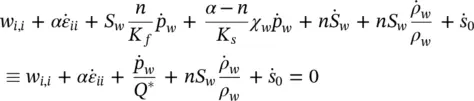

or

(2.30b)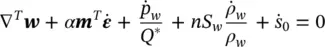

Now, however, Q *is different from that given in Equation 2.17and we have in its place

(2.30c)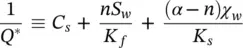

which, of course, must be identical with ( 2.17) when S w= 1 and χ w= 1, i.e. when we have full saturation. The above modification is mainly due to an additional term to those defining the increased storage in ( 2.17). This term is due to the changes in the degree of saturation and is simply:

(2.31)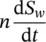

but here we introduce a new parameter C Sdefined as

(2.32)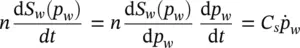

The final elimination of win a manner identical to that used when deriving (2.21) gives (neglecting density variation):

(2.33a)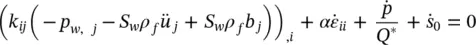

or

(2.33b)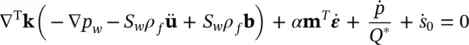

The small changes required here in the solution process are such that we found it useful to construct our computer program for the partially saturated form, with the fully saturated form being a special case.

In the time‐stepping computation, we still always assume that the parameters S w, k w, and C schange slowly and hence we will compute these at the start of the time interval keeping them subsequently constant.

Previously, we mentioned several typical cases where pressure can become negative and hence saturation drops below unity. One frequently encountered example is that of the flow occurring in the capillary zone during steady‐state seepage . The solution to the problem can, of course, be obtained from the general equations simply by neglecting all acceleration and fixing the solid displacements at zero (or constant) values.

If we consider a typical dam or a water‐retaining embankment shown in Figure 2.3, we note that, on all the surfaces exposed to air, we have apparently incompatible boundary conditions. These are:

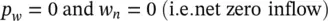
Clearly, both conditions cannot be simultaneously satisfied and it is readily concluded that only the second is true above the area where the flow emerges. Of course, when the flow leaves the free surface, the reverse is true.

Computation will easily show that negative pressures develop near the surface and that, therefore, a partially saturated zone with very low permeability must exist. The result of such a computation is shown in Figure 2.3and indeed it will be found that very little flow occurs above the zero‐pressure contour. This contour is, in fact, the well‐known Phreatic line and the partially saturated material procedure has indeed been used frequently purely as a numerical device for its determination (see Desai 1977a, 1977b; Desai and Li 1983 etc.). Another example is given in Figure 2.4. Here a numerical solution of Zienkiewicz et al. (1990b) is given for a problem for which experimental data are available from Liakopoulos (1965).