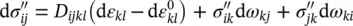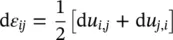The notation used throughout this chapter will generally be of standard, tensorial form. Thus:
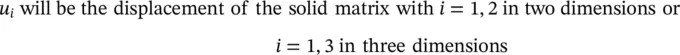
Alternatively, the form
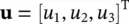
will also be used for the same quantity in vectorial notation.
Similarly, we shall use w iand v ior wand vto denote the velocities of water and air relative to the solid components. These velocities are calculated on the basis of dividing the appropriate flow by the total cross sectional area of the solid–fluid composite.
As mentioned in Chapter 1, σ ijand 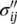 refer to the appropriate total and effective stresses, with σand σ ″ being the vectorial alternatives.
refer to the appropriate total and effective stresses, with σand σ ″ being the vectorial alternatives.
Similarly, ε ijor ε refers to the strain components. Further, p a, p w, and p = χ w p w+ χ a p awill stand for air and water pressure and the “effective” pressure defined in the effective stress concept in Equation (1.11) when two fluids are present.
S aand S ware the relative degrees of saturation and k aand k ware the permeabilities for air and water flow.
Other symbols will be added and defined in the text as the need arises.
The derivation of the equations in this chapter follows a physical approach which establishes clearly the interactions involved in the manner presented by Zienkiewicz and Shiomi (1984), Zienkiewicz (1982), Zienkiewicz et al. (1990a, 1990b), etc. This is a slightly different approach from that used in the earlier presentations of Biot (1941, 1955, 1956a, 1956b, 1962) and Biot and Willis (1957) but we believe it is slightly easier to follow as it explores the physical meaning of each term.
Later, it became fashionable to derive the equations in the form of the so‐called mixture theories (see Green and Adkin 1960; Green 1969; Bowen 1976). The equations derived were subsequently recast in varying forms. Here an important step forward was introduced by Morland (1972) who used extensively the concept of volume fractions. Derski (1978) introduced a different derivation of coupled equations and Kowalski (1979) compared various parameters occurring in Derski’s equations with those of Biot’s equations. A full discussion of the development of the theory is given in the paper by de Boer (1996).
For completeness, we shall include such mixture derivations of the equations in Section 2.5. If correctly applied, the mixture theory establishes, of course, identical equations with appropriately chosen parameters and rheological relations.
It seems that despite much sophistication of various sets of coupled equations, most authors limited their works to conventional, linear elastic, behavior of the solid. Indeed, de Boer and Kowalski (1983) found it necessary to develop a special plasticity theory for porous, saturated solids. In the equations of Zienkiewicz (1982) and Zienkiewicz et al. (1990a), any nonlinear behavior can be specified for the skeleton and, therefore, realistic models can be incorporated. Indeed we shall find that such models are essential if practical conclusions are to be drawn from this work.
2.2 Fully Saturated Behavior with a Single Pore Fluid (Water)
2.2.1 Equilibrium and Mass Balance Relationship ( u , w , and p )
We recall first the effective stress and constitutive relationships as defined in Equation (1.16) of Chapter 1which we repeat below.
(2.1a) 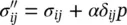
or
(2.1b) 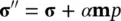
This effective stress is conveniently used as it can be directly established from the total strains developed.
However, it should be remembered here that this stress definition was derived in Chapter 1as a corollary of using the effective stress defined as below:
(2.2a) 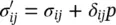
or
(2.2b) 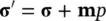
which is responsible for the major part of the deformation and certainly for failure.
In soils, the difference between the two effective stresses is negligible as α ≈ 1. However, for such materials as concrete or rock, the value of α in the first expression can be as low as 0.5 but experiments on tensile strength show that the second definition of effective stress is there much more closely applicable as shown by Leliavsky (1947), Serafim (1954), etc.
For soil mechanics problems, to which we will devote most of the examples, α = 1 will be assumed. Constitutive relationships will still, however, be written in the general form using an incremental definition
(2.3a) 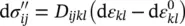
(2.3b) 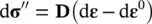
The vectorial notation used here follows that corresponding to stress components given in (1.1). We thus define the strains as
(2.4) 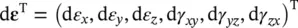
In the above, Dis the “tangent matrix” and d ε 0is the increment of the thermal or similar autogenous strain and of the grain compression 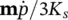 . The latter is generally neglected in soil problems.
. The latter is generally neglected in soil problems.
If large strains are encountered, this definition needs to be modified and we must write
(2.5) 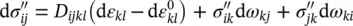
where the last two terms account for simple rotation (via the definition in 2.6b) of the existing stress components and are known as the Zaremba (1903a, 1903b)–Jaumann (1905) stress changes. We omit here the corresponding vectorial notation as this is not easy to implement.
The large strain rotation components are small for small displacement computation and can be frequently neglected. Thus, in the derivations that follow, we shall do so – though their inclusion presents no additional computational difficulties.
The strain and rotation increments of the soil matrix can be determined in terms of displacement increments d u ias
(2.6a) 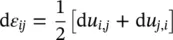
Читать дальше

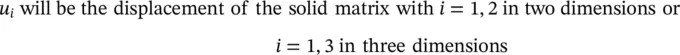
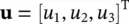
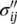 refer to the appropriate total and effective stresses, with σand σ ″ being the vectorial alternatives.
refer to the appropriate total and effective stresses, with σand σ ″ being the vectorial alternatives.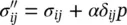
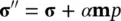
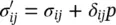
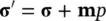
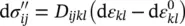
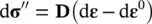
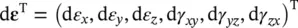
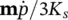 . The latter is generally neglected in soil problems.
. The latter is generally neglected in soil problems.