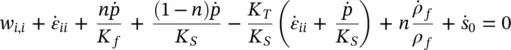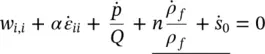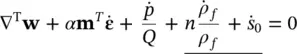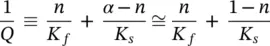and
(2.6b) 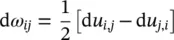
The comma in the suffix denotes differentiation with respect to the appropriate coordinate specified. Thus
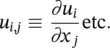
If the vectorial notation is used, as is often the case in the finite element analysis, the so‐called engineering strains are used in which (with the repeated index of ∂ u i,inot summed)
(2.7a) 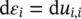
or

However, the shear strain increments will be written as
(2.7b) 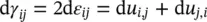
or
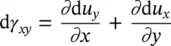
We shall usually write the process of strain computation using matrix notation as
(2.8) 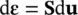
where
(2.9) 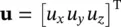
And for two dimensions, the strain matrix is defined as:
(2.10) 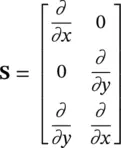
with corresponding changes for three dimensions (as shown in Zienkiewicz et al. 2005).
We can now write the overall equilibrium or momentum balance relation for the soil–fluid “mixture” as
(2.11a) 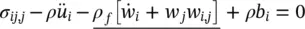
or
(2.11b) 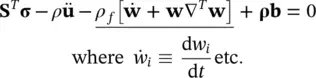
In the above, w i(or w) is the average (Darcy) velocity of the percolating water.
The underlined terms in the above equation represent the fluid acceleration relative to the solid and the convective terms of this acceleration. This acceleration is generally small and we shall frequently omit it. In derivations of the above equation, we consider the solid skeleton and the fluid embraced by the usual control volume: d x ⋅ d y ⋅ d z .
Further, ρ fis the density of the fluid, bis the body force per unit mass (generally gravity) vector, and ρ is the density of the total composite, i.e.
(2.12) 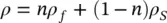
where ρ Sis the density of the solid particles and n is the porosity (i.e. the volume of pores in a unit volume of the soil).
The second equilibrium equation ensures the momentum balance of the fluid. If again we consider the same unit control volume as that assumed in deriving (2.11) (and we further assume that this moves with the solid phase), we can write
(2.13a) 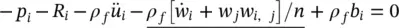
or
(2.13b) 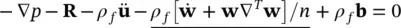
In the above, we consider only the balance of the fluid momentum and Rrepresents the viscous drag forces which, assuming the Darcy seepage law, can be written as
(2.14a) 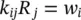
(2.14b) 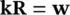
Note that the underlined terms in (2.13) represent again the convective fluid acceleration and are generally small. Also note that, throughout this book, the permeability kis used with dimensions of [length] 3·[time]/[mass] which is different from the usual soil mechanics convention k′ which has the dimension of velocity, i.e. [length]/[time]. Their values are related by 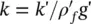 where
where 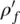 and g′ are the fluid density and gravitational acceleration at which the permeability is measured.
and g′ are the fluid density and gravitational acceleration at which the permeability is measured.
The final equation is one accounting for the mass balance of the flow. Here we balance the flow divergence w iiby the augmented storage in the pores of a unit volume of soil occurring in time d t . This storage is composed of several components given below in order of importance:
1 the increased volume due to a change in strain, i.e.: δijdεij = dεii = mTdε
2 the additional volume stored by compression of void fluid due to fluid pressure increase: ndp/Kf
3 the additional volume stored by the compression of grains by the fluid pressure increase: (1 − n)dp/KSand
4 the change in volume of the solid phase due to a change in the intergranular effective contact stress .
Here K Tis the average bulk modulus of the solid skeleton and ε iithe total volumetric strain.
Adding all the above contributions together with a source term and a second‐order term due to the change in fluid density in the process, we can finally write the flow conservation equation
(2.15) 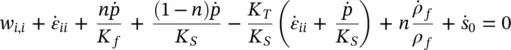
This can be rewritten using the definition of α given in Equation (1.15b)as
(2.16a) 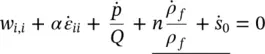
or in vectorial form
(2.16b) 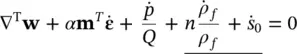
where
(2.17) 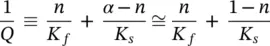
In (2.16), the last two (underlined) terms are those corresponding to a change of density and rate of volume expansion of the solid in the case of thermal changes and are negligible in general. We shall omit them from further consideration here.
Читать дальше

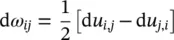
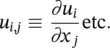
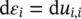

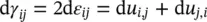
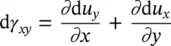
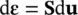
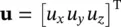
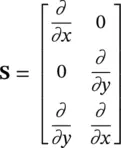
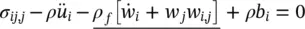
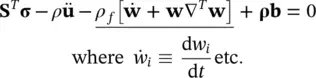
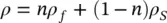
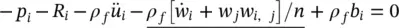
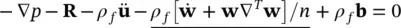
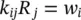
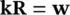
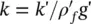 where
where 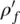 and g′ are the fluid density and gravitational acceleration at which the permeability is measured.
and g′ are the fluid density and gravitational acceleration at which the permeability is measured.