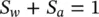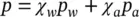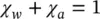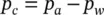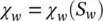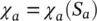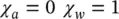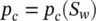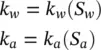Manuel Pastor - Computational Geomechanics

recovering the common definition used by many in soil mechanics and introduced by Terzaghi (1936). Now, however, the meaning of α is no longer associated with an effective area.

It should have been noted that in some materials such as rocks or concrete, it is possible for the ratio K T/ K sto be as large as 1/3 with α = 2/3 being a fairly common value for determination of deformation.

We note that in the preceding discussion, the only assumption made, which can be questioned, is that of neglecting the local damage due to differing materials in the soil matrix. We have also implicitly assumed that the fluid flow is such that it does not separate the contacts of the soil grains. This assumption is not totally correct in soil liquefaction or flow in the soil‐shearing layer during localization; therefore, it is not clear if Terzaghi’s definition of effective stress still applies when the soil is liquefied.

The interstitial space, or the pores, may, in a practical situation, be filled with two or more fluids. We shall, in this section, consider only two fluids with the degree of saturation by each fluid being defined by the proportion of the total pore volume n (porosity) occupied by each fluid. In the context of soil behavior discussed in this book, the fluids will invariably be water and air , respectively. Thus, we shall refer to only two saturation degrees, S wthat for water and S athat for air, but the discussion will be valid for any two fluids.

It is clear that if both fluids fill the pores completely, we shall always have

(1.18)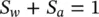

Clearly, this relation will be valid for any other pair of fluids, e.g. oil and water and indeed the treatment described here is valid for any fluid conditions.

The two fluids may well present different areas of contact with the solid grains of the material in the manner illustrated in Figure 1.5a and b. The average pressure reducing the interstitial contact and relevant to the definition of effective stress found in the previous section (Equations (1.16) and (1.17)) can thus be taken as

(1.19)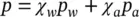

where the coefficients χ wand χ arefer to water and air, respectively, and are such that

(1.20)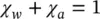

The individual pressures p wand p aare again referring to water and air and their difference, i.e.

(1.21)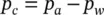

is dependent on the magnitude of surface tension or capillarity and on the degree of saturation ( p cis often referred to, therefore, as capillary pressure).

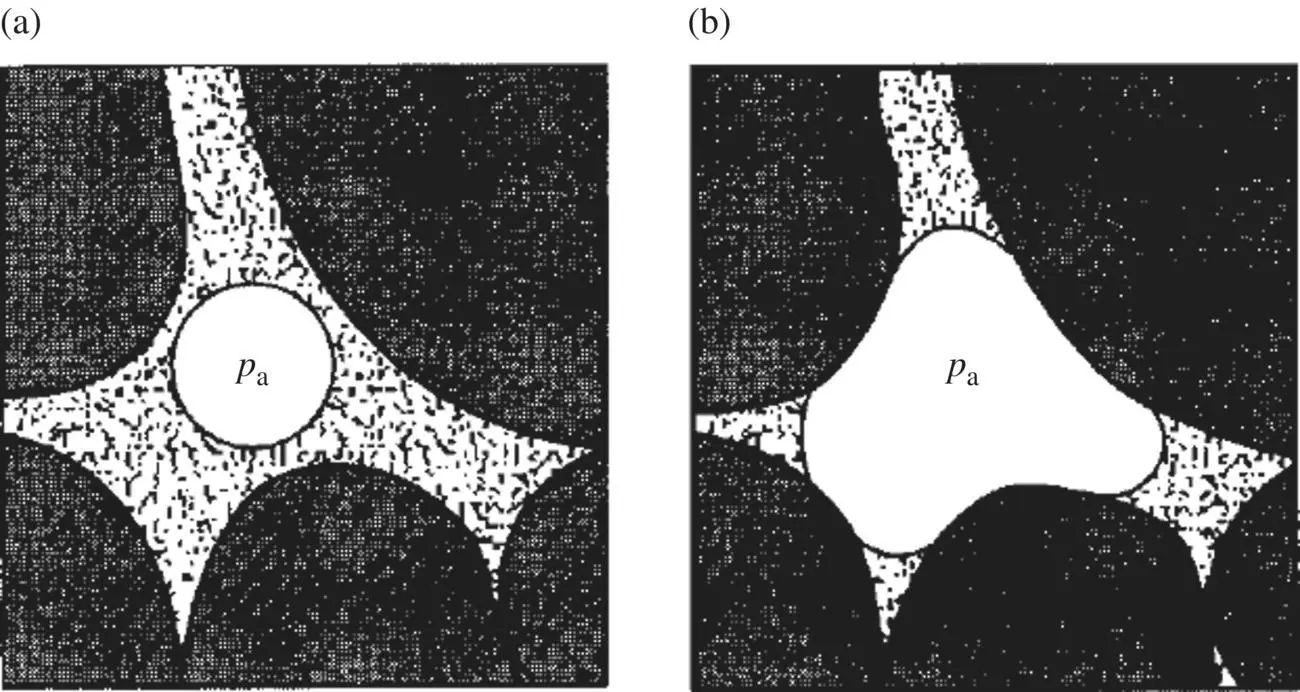
Figure 1.5 Two fluids in pores of a granular solid (water and air). (a) Air bubble not wetting solid surface (effective pressure p = p w); (b) Both fluids in contact with solid surfaces (effective pressure p = χ w p w+ χ a p a).

Depending on the nature of the material surface, the contact surface may take on the shapes shown in Figure 1.5with

(1.22a)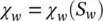

and

(1.22b)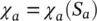

Occasionally, the contact of one of the phases and the solid may disappear entirely as shown in Figure 1.5a giving isolated air bubbles and making in this limit

(1.23)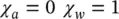

In many situations, in soil mechanics, it is sufficient to take χ equal to the respective degrees of saturation (Lewis and Schrefler 1982; Nuth and Laloui 2008).

Whatever the nature of the contact, we shall find, neglecting the hysteresis during the wetting and drying cycles, that a unique relationship between p cand the saturation S wcan be written, i.e.

(1.24)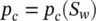

Indeed, the degree of saturation will similarly affect flow parameters such as the permeability k to which we shall make reference in the next chapter, giving

(1.25)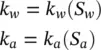

Many studies of such relationship are reported in the literature (Liakopoulos 1965; Neuman 2017; Van Genuchten et al. 1977; Narasimhan and Witherspoon 1978; Safai and Pinder 1979; Lloret and Alonso 1980; Bear et al. 1984; Alonso et al. 1987). Figure 1.6shows a typical relationship.

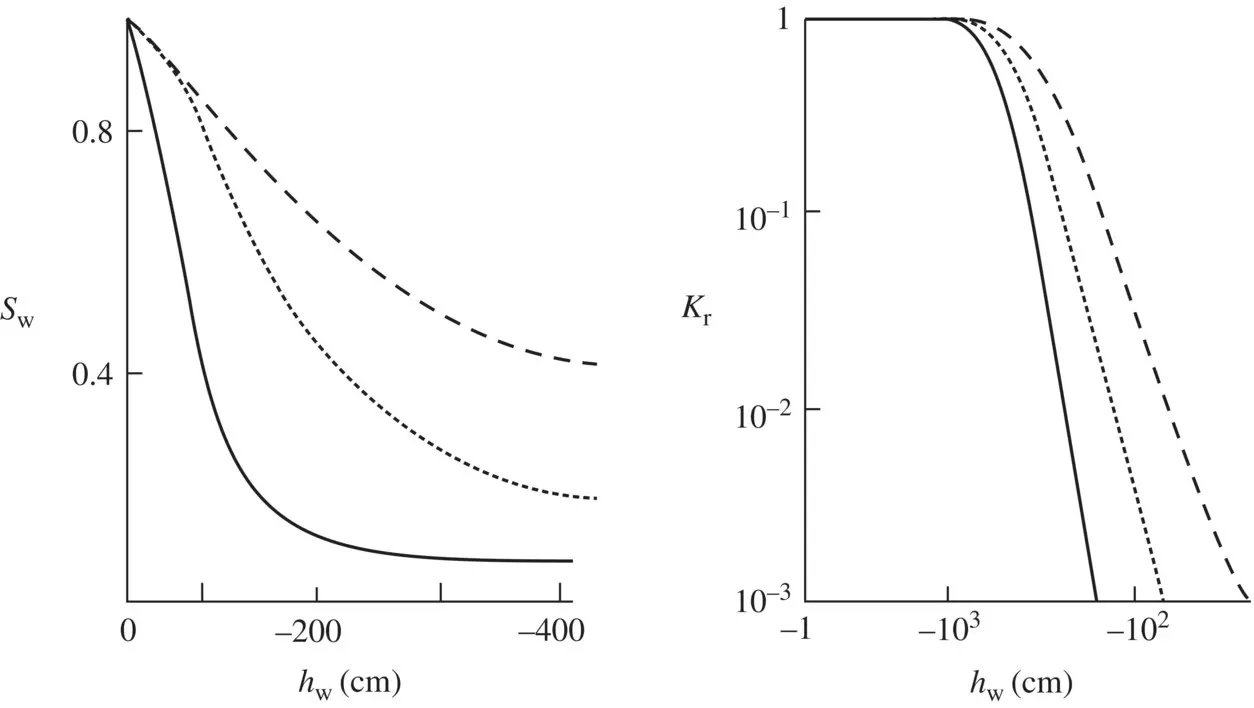
Figure 1.6 Typical relations between pore pressure head, h w= p w/ χ w, saturation, S w, and relative permeability, k r= k w( S w)/ k w(1) (Safai and Pinder 1979). Note that relative permeability decreases very rapidly as saturation decreases.

Source: From Safai and Pinder (1979).

The concepts of dealing with the effects of multiple pore pressure by introducing an average pressure and using the standard definition of effective stress ( 1.19, 1.16, and 1.17) were first introduced by Bishop (1959). Certainly, the arguments for thus extending the original concepts are less clear than is the case when only a single fluid is present. However, the results obtained by this extension are quite accurate. We shall, therefore, use such a definition in the study of partially saturated media.

In many cases occurring in practice, the air pressure is close to zero (atmospheric datum) as the pores are interconnected. Alternatively, negative air pressure occurs as cavitation starts and here the datum is the vapor pressure of water. In either case, the effect of p acan be easily neglected as the water pressure simply becomes negative from Equation (1.24). Such negative pressures are responsible for the development of certain cohesion by the soil and are essential in the study of free surface conditions occurring in embankments, as we shall see later.

1 1 Such strength reduction phenomena are mainly evident in essentially non‐cohesive materials such as sand and silt. Clays in which negative capillary pressure provide an apparent cohesion are less liable to such strength reduction.